Database-Management-System
October 14, 2023NTA-UGC-NET 2021 Dec & 2022 June Paper-2
October 14, 2023Algorithms
| Question 26 |
Consider a simple undirected weighted graph G , all of whose edge weights are distinct. Which of the following statements about the minimum spanning trees of G is/are TRUE?
| The edge with the second smallest weight is always part of any minimum spanning tree of G . | |
| One or both of the edges with the third smallest and the fourth smallest weights are part of any minimum spanning tree of G . | |
 | |
| G can have multiple minimum spanning trees. |
Question 26 Explanation:
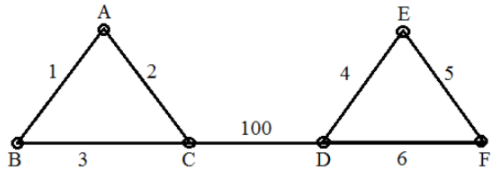
Let assume the graph and minimum spanning tree of the corresponding graph.


Option-A: TRUE: As per the above graph, the second minimum edge weight is also part of the MST.
The second smallest weight is always in MST because it will not form a cycle.
Option-B: TRUE: Graph G is having more than 4 vertices. Suppose 3rd smallest element is forming a cycle then it takes 4th smallest element. So, the given statement is TRUE.
Option-C: TRUE: As per the example graph, it is always correct.
Option-D: FALSE: We will get a unique minimum spanning tree if edge weights are distinct.

Option-A: TRUE: As per the above graph, the second minimum edge weight is also part of the MST.
The second smallest weight is always in MST because it will not form a cycle.
Option-B: TRUE: Graph G is having more than 4 vertices. Suppose 3rd smallest element is forming a cycle then it takes 4th smallest element. So, the given statement is TRUE.
Option-C: TRUE: As per the example graph, it is always correct.
Option-D: FALSE: We will get a unique minimum spanning tree if edge weights are distinct.
Correct Answer: C
Question 26 Explanation:
Let assume the graph and minimum spanning tree of the corresponding graph.


Option-A: TRUE: As per the above graph, the second minimum edge weight is also part of the MST.
The second smallest weight is always in MST because it will not form a cycle.
Option-B: TRUE: Graph G is having more than 4 vertices. Suppose 3rd smallest element is forming a cycle then it takes 4th smallest element. So, the given statement is TRUE.
Option-C: TRUE: As per the example graph, it is always correct.
Option-D: FALSE: We will get a unique minimum spanning tree if edge weights are distinct.


Option-A: TRUE: As per the above graph, the second minimum edge weight is also part of the MST.
The second smallest weight is always in MST because it will not form a cycle.
Option-B: TRUE: Graph G is having more than 4 vertices. Suppose 3rd smallest element is forming a cycle then it takes 4th smallest element. So, the given statement is TRUE.
Option-C: TRUE: As per the example graph, it is always correct.
Option-D: FALSE: We will get a unique minimum spanning tree if edge weights are distinct.
Subscribe
Login
0 Comments
