GATE 2011
October 26, 2023NTA-UGC-NET 2021 Dec & 2022 June Paper-2
October 26, 2023GATE 2011
| Question 52 |
An undirected graph G(V, E) contains n (n > 2) nodes named v1, v2, ….vn. Two nodes vi , vj are connected if and only if 0 < |i – j| ≤ 2. Each edge (vi, vj) is assigned a weight i + j. A sample graph with n = 4 is shown below.
What will be the cost of the minimum spanning tree (MST) of such a graph with n nodes?
| 1/12(11n2-5n) | |
| n2 – n + 1 | |
| 6n – 11 | |
| 2n + 1 |
Question 52 Explanation:
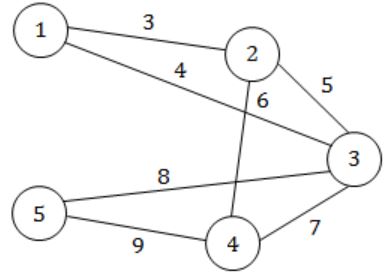
Let take example of 5 vertices,

Cost of MST,

= 3+4+6+8 = 21
Only option (B) satisfies it.
Cost of MST,
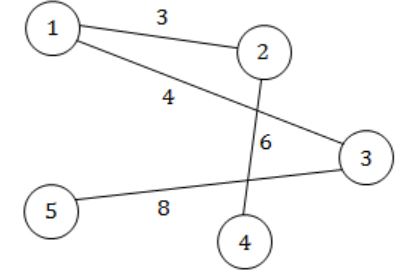
= 3+4+6+8 = 21
Only option (B) satisfies it.
Correct Answer: B
Question 52 Explanation:
Let take example of 5 vertices,

Cost of MST,

= 3+4+6+8 = 21
Only option (B) satisfies it.

Cost of MST,

= 3+4+6+8 = 21
Only option (B) satisfies it.
Subscribe
Login
0 Comments

