Question 7660 – Reading-Comprehension
December 11, 2023UGC NET CS 2015 Dec – paper-3
December 11, 2023GATE 2010
| Question 1 |
Let G = (V,E) be a graph. Define ξ(G) = Σd id x d, where id is the number of vertices of degree d in G. If S and T are two different trees with ξ(S) = ξ(T),then
| |S| = 2|T| | |
| |S| = |T| – 1 | |
| |S| = |T| | |
| |S| = |T| + 1 |
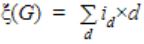
id= no. of vertices of degree ‘d’ in ‘G’
Eg:
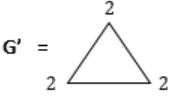
No. of vertices with degree ‘2’ = 3
ξ(G’) = 3 × 2 = ‘6’ i.e., sum of degrees
By Handshaking Theorem,
The sum of degrees would be equal to twice the no. of edges
|V| = 2|E|
It is given that ξ(G) = ξ(S) then
Sum of degrees of vertices in G is equal to sum of degrees of vertices in S
i.e., 2*(no. of edges in G) = 2*no. of edges in S
no. of edges in G = no. of edges in S
Eg:
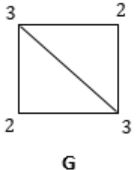
ξ(G) = (2 × 2) + (2 × 3) = 4 + 6 = 10
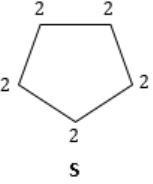
ξ(S) = 2 × 5 = 10
You can observe that, though no. of vertices are different, but still no. of edges are same.
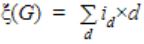
id= no. of vertices of degree ‘d’ in ‘G’
Eg:
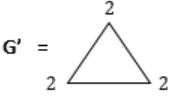
No. of vertices with degree ‘2’ = 3
ξ(G’) = 3 × 2 = ‘6’ i.e., sum of degrees
By Handshaking Theorem,
The sum of degrees would be equal to twice the no. of edges
|V| = 2|E|
It is given that ξ(G) = ξ(S) then
Sum of degrees of vertices in G is equal to sum of degrees of vertices in S
i.e., 2*(no. of edges in G) = 2*no. of edges in S
no. of edges in G = no. of edges in S
Eg:
ξ(G) = (2 × 2) + (2 × 3) = 4 + 6 = 10
ξ(S) = 2 × 5 = 10
You can observe that, though no. of vertices are different, but still no. of edges are same.