Question 3893 – 2009 December UGC NET Paper 1
February 13, 2024GATE 1990
February 13, 2024GATE 1990
| Question 11 |
Choose the correct alternatives (More than one may be correct).
The number of rooted binary trees with n nodes is,
| Equal to the number of ways of multiplying (n+1) matrices. | |
| Equal to the number of ways of arranging n out of 2n distinct elements. | |
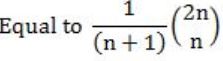 | |
| Equal to n! | |
| Both (A) and (C). |
Question 11 Explanation:
No. of rooted binary trees (unlabeled) with n nodes is given by nth catalan number which equals (2nCn)/(n+1)
Here, both options A and C are true as option A corresponds to n multiply operations of (n+1) matrices, the no. of ways for this is again given by the nth catalan number.
Here, both options A and C are true as option A corresponds to n multiply operations of (n+1) matrices, the no. of ways for this is again given by the nth catalan number.
Correct Answer: E
Question 11 Explanation:
No. of rooted binary trees (unlabeled) with n nodes is given by nth catalan number which equals (2nCn)/(n+1)
Here, both options A and C are true as option A corresponds to n multiply operations of (n+1) matrices, the no. of ways for this is again given by the nth catalan number.
Here, both options A and C are true as option A corresponds to n multiply operations of (n+1) matrices, the no. of ways for this is again given by the nth catalan number.
