Database-Management-System

Question 566

The maximum number of keys stored in a B-tree of order m and depth d is

A	md+1–1
B	(md+1–1) / (m–1)
C	(m–1) (md+1–1)
D	(md–1) / (m–1)
E	None of the above

Database-Management-SystemB-and-B+-TreesUGC NET CS 2012 Dec-Paper-2

Question 566 Explanation:

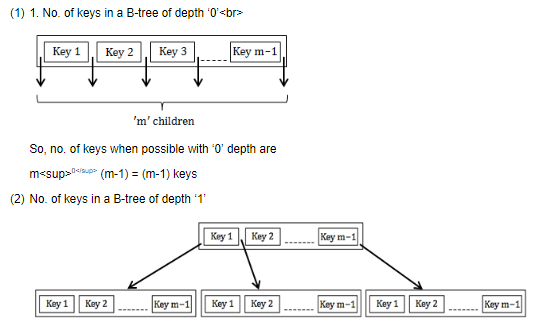
Order of a B-tree represents the number of children a node can have and we know the number of keys is always equals to the (Order of B-tree) – 1

So here each of the ‘m’ children is having (m-1) keys.
Hence total no. of keys = m¹ (m-1) keys
(3) Similarly, for a B-tree of order ‘d’ total no. of keys possible = m^d (m-1) keys

Correct Answer: E

Question 566 Explanation:

Order of a B-tree represents the number of children a node can have and we know the number of keys is always equals to the (Order of B-tree) – 1

So here each of the ‘m’ children is having (m-1) keys.
Hence total no. of keys = m¹ (m-1) keys
(3) Similarly, for a B-tree of order ‘d’ total no. of keys possible = m^d (m-1) keys