Theory-of-Computation
October 22, 2023Database-Management-System
October 22, 2023Time-Complexity
|
Question 22
|
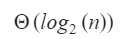 |
|
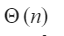 |
|
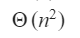 |
|
 |
In this question they given three main constraints
- The input array is in sorted order
- Use recursive binary search
- Worst case number of operations
If the array is in sorted order then the worst case time complexity is O(logn)
Ex: 10, 20, 30
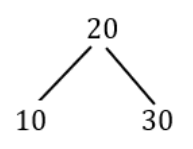
The binary search approach is using either recursive or iterative method is
Step-1: element = middle, the element is found and return the index.
Step-2: element > middle, search for the element in the sub-array starting from middle+1 index to n.
Step-3: element < middle, search for element in the sub-array starting from 0 index to middle -1.
Note: The worst case happens when we want to find the smallest/largest farthest node. So, it will not take more than O(logn) time.
In this question they given three main constraints
- The input array is in sorted order
- Use recursive binary search
- Worst case number of operations
If the array is in sorted order then the worst case time complexity is O(logn)
Ex: 10, 20, 30

The binary search approach is using either recursive or iterative method is
Step-1: element = middle, the element is found and return the index.
Step-2: element > middle, search for the element in the sub-array starting from middle+1 index to n.
Step-3: element < middle, search for element in the sub-array starting from 0 index to middle -1.
Note: The worst case happens when we want to find the smallest/largest farthest node. So, it will not take more than O(logn) time.
