GATE 2007
October 24, 2023GATE 2007
October 24, 2023GATE 2007
| Question 13 |
The maximum number of binary trees that can be formed with three unlabeled nodes is:
| 1 | |
| 5 | |
| 4 | |
| 3 |
Question 13 Explanation:
Total number of binary trees possible for n nodes is
C(n) = (2n)!/(n+1)!n!
C(n) = (2(3))!/(3+1)!3! = 6×5×4×3×2×1/4×3×2×1×3×2 = 5
Total no. of possible trees is 5.

Total = 5
C(n) = (2n)!/(n+1)!n!
C(n) = (2(3))!/(3+1)!3! = 6×5×4×3×2×1/4×3×2×1×3×2 = 5
Total no. of possible trees is 5.
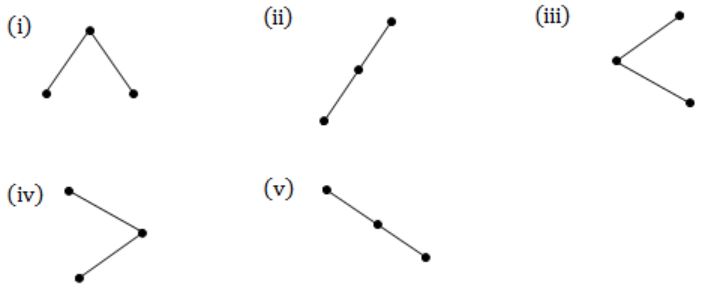
Total = 5
Correct Answer: B
Question 13 Explanation:
Total number of binary trees possible for n nodes is
C(n) = (2n)!/(n+1)!n!
C(n) = (2(3))!/(3+1)!3! = 6×5×4×3×2×1/4×3×2×1×3×2 = 5
Total no. of possible trees is 5.

Total = 5
C(n) = (2n)!/(n+1)!n!
C(n) = (2(3))!/(3+1)!3! = 6×5×4×3×2×1/4×3×2×1×3×2 = 5
Total no. of possible trees is 5.

Total = 5
Subscribe
Login
0 Comments
