Question 1 |
For merging two sorted lists of sizes m and n into a sorted list of size m+n, we required comparisons of
A | O(m) |
B | O(n) |
C | O(m+n) |
D | O(logm+logn) |
In worst case, no. of comparisons is m+n-1.
Then we require O(m+n) comparisons to merging two sorted lists.
Question 2 |
A binary tree T has n leaf nodes. The number of nodes of degree 2 in T is:
A | log2 n |
B | n - 1 |
C | n |
D | 2n |
The no. of subtrees of a node is called the degree of the node. In a binary tree, all nodes have degree 0, 1 and 2.
The degree of a tree is the maximum degree of a node in the tree. A binary tree is of degree 2.
The number of nodes of degree 2 in T is "n - 1".
Question 3 |
A D flip-flop is to be connected to an 8085 microprocessor chip as a 1-bit output port with a port address of FF hex. Data bit D3 should be involved in the data transfer from CPU to the flip-flop. The flip-flop should be cleared on power ON.
(a) Using only one NAND gate (fan in of 10), one NOT gate and one D flip-flop. Draw the required interface logic circuit (only the relevant signals should be shown).
(b) Write a program to generate a square wave on the output of the flip-flop. ON and OFF periods of the square wave should be 7 bus cycles each.
A | Theory Explanation. |
Question 4 |
Let L = {a1, a2, ......, an} n ≥ 0 be a list whose Pascal representation is
type list = record
next: ↑ list; val: integer end The following function returns a list in which a2i and a2i-1, 1 ≤ i ≤ [n/2] are interchanged. Complete the function by filling the boxes. Write the line number and the content of the box in your answer sheet.
1. function change (p: ↑ list): ↑ list; 2. var q.t: ↑ list; 3. begin 4. if p = nil then change := p 5. else if p ↑ next = nil then change : ▭ 6. else begin 7. q : p ↑ next; 8. ▭ := q; 9. t : q ↑ next; 10. ▭ := p; 11. ▭ := change(t) 12. end 13. end
A | Theory Explanation. |
Question 5 |
Consider a graph whose vertices are points in the plane with integer co-ordinates (x,y) such that 1≤x≤n and 1≤y≤n, where n≥2 is an integer. Two vertices (x1,y1) and (x2,y2) are adjacent iff ∣x1−x2∣ ≤ 1 and ∣y1–y2∣ ≤1. The weight of an edge {(x1,y1),(x2,y2)} is √(x1–x2)2 + (y1–y2)2
(a) What is the weight of a minimum weight-spanning tree in this graph? Write only the answer without any explanations.
(b) What is the weight of a maximum weight-spanning tree in this graph? Write only the answer without any explanations.
A | Theory Explanation. |
Question 6 |
Consider the following program in Pseudo-Pascal syntax.
program what: var z: integer
procedure recur(x):
begin if x <= 40 then
begin x:x+z
recur(x);
z:=x+10
end
end(*recur*)
begin(*what*)
z=10;
recur(z);
writeln(z)
end (a) Suppose the parameter to the procedure ‘recur’ is passed by value.
i. What value is printed by program?
ii. How many times is ‘recur’ called?
(b) What value is printed by the program if the parameter is passed by reference?
A | Theory Explanation. |
Question 7 |
Consider the grammar
S → bSe S → PQR P → bPc P → ε Q → cQd Q → ε R → dRe R → ε
where S,P,Q,R are non-terminal symbols with S being the start symbol; b,c,d,e are terminal symbols and ‘ε’ is the empty string. This grammar generates strings of the form bi, cj, dk, em for some i,j,k,m ≥ 0.
(a) What is the condition on the values of i,j,k,m?
(b) Find the smallest string that has two parse trees.
A | Theory Explanation. |
Question 8 |
Consider a hash table with n buckets, where external (overflow) chaining is used to resolve collisions. The hash function is such that the probability that a key value is hashed to a particular bucket is 1/n. The hash table is initially empty and K distinct values are inserted in the table.
(a) What is the probability that bucket number 1 is empty after the Kth insertion?
(b) What is the probability that no collision has occurred in any of the K insertions?
(c) What is the probability that the first collision occurs at the Kth insertions?
A | Theory Explanation. |
Question 9 |
Let F be the set of one-to-one functions from the set {1,2,…,n} to the set {1,2,…,m}, where m≥n≥1.
(a) How many functions are members of F?
(b) How many functions f in F satisfy the property f(i) = 1 for some i, 1≤i≤n?
(c) How many functions f in F satisfy the property f(i) < f(j) for all 1≤i≤j≤n?
A | Theory Explanation. |
Question 10 |
Let R be a reflexive and transitive relation on a set A. Define a new relation E on A as
E = {(a,b) ∣ (a,b)∈R and (b,a)∈R} (a) Prove that E is an equivalence relation on A.
(b) Define a reason ≤ on the equivalence classes of E as E1 ≤ E2 if ∃a,b such that a∈E1, b∈E2 and (a,b)∈R. Prove that ≤ is a partial order.
A | Theory Explanation. |
Question 11 |
Consider the following function.
Function F (n, m: integer): integer;
begin
If (n <= 0) or (m <= 0) then F:=1
else
F:= F(n-1, m) + F(n, m-1);
end; Use the recurrence relation to answer the following question. Assume that n, m are positive integers. Write only the answers without any explanation.
(a) What is the value of F(n,2)?
(b) What is the value of (n,m)?
(c) How many recursive calls are made to the function F, including the original call, when evaluating F(n,m).
A | Theory Explanation. |
Question 12 |
A size-balanced binary tree is a binary tree in which for every node, the difference between the number of nodes in the left and right subtree is at most 1. The distance of a node from the root is the length of the path from the root to the node. The height of a binary tree is the maximum distance of a leaf node from the root.
(a) Prove, by using induction on h, that a size-balance binary tree of height h contains at least 2h nodes.
(b) In a size-balanced binary tree of height h≤1, how many nodes are at distance h−1 from the root? Write only the answer without any explanations.
A | Theory Explanation. |
Question 13 |
An array A contains n≥1 positive integers in the locations A[1], A[2],... A[n]. The following program fragment prints the length of a shortest sequence of consecutive elements of A, A[i], A[i+1],...A[j] such that the sum of their values is ≥M, a given positive number. It prints ‘n+1’ if no such sequence exists. Complete the program by filling in the boxes. In each case use the simplest possible expression. Write only the line number and the contents of the box.
1. begin 2. i: +1; j:=1; 3. Sum := ▭; 4. min: n; finish:=false; 5. While not finish do 6. If ▭ then 7. if j=n then finish:=true. 8. else 9. begin 10. j:=j+1; 11. sum:=▭ 12. end 13. else 14. begin 15. If(j-1) < min then min:=j-1; 16. sum:=sum - A[i]; 17. i:=i+1; 18. end 19. writeln (min+1); 20. end.
A | Theory Explanation. |
Question 14 |
Consider the following piece of 'C' code fragment that removes duplicates from an ordered list of integers.
Node *remove-duplicates(Node *head, int *j)
{
Node *t1, *t2;
*j=0;
t1 = head;
if (t1! = NULL) t2 = t1 →next;
else return head;
*j = 1;
if(t2 == NULL) return head;
while t2 != NULL)
{
if (t1.val != t2.val) --------------------------→ (S1)
{
(*j)++; t1 → next = t2; t1 = t2: ----------→ (S2)
}
t2 = t2 → next;
}
t1 → next = NULL;
return head;
} Assume the list contains n elements (n≥2) in the following questions.
(a) How many times is the comparison in statement S1 made?
(b) What is the minimum and the maximum number of times statements marked S2 get executed?
(c) What is the significance of the value in the integer pointed to by j when the function completes?
A | Theory Explanation. |
Question 15 |
A B+ - tree of order d is a tree in which each internal node has between d and 2d key values. An internal node with M key values has M+1 children. The root (if it is an internal node) has between 1 and 2d key values. The distance of a node from the root is the length of the path from the root to the node. All leaves are at the same distance from the root. The height of the tree is the distance of a leaf from the root.
(a) What is the total number of key values in the internal nodes of a B+ - tree with l leaves (l≥2)?
(b) What is the maximum number of internal nodes in a B+ - tree of order 4 with 52 leaves?
(c) What is the minimum number of leaves in a B+ - tree of order d and height h(h≥1)?
A | Theory Explanation. |
Question 16 |
Construct a finite state machine with minimum number of states, accepting all strings over {a,b} such that the number of a's is divisible by two and the number of b's is divisible by three.
A | Theory Explanation. |
Question 17 |
Given that L is a language accepted by a finite state machine, show that LP and LR are also accepted by some finite state machines, where
LP = {s|ss' ∈ L, for some string s'}
LR = {s|s obtainable by reversing some string in L}
A | Theory Explanation. |
Question 18 |
A language L is a subset of Pascal with the following constructs:
- (a) Expressions involving the operators '+' and '<' only
(b) Assignment statements
(c) 'while' statements and
(d) Compound statements with the syntax 'begin...end'
Give an unambiguous grammar for L.
A | Theory Explanation. |
Question 19 |
The language L, defined by the following grammar allows use of real or integer data in expressions and assignment statements.
(assign-stmt):: = (LHS):= (E)
(E) :: = (E) + (T)|(T)
(T) :: = (T) * (V)|(V)
(V) :: = id|((E))
(LHS) :: = id It is required to convert expression and assignment strings of L into postfix strings that use the type-specific operators (+, i), (+, r), (*, i), (*, r), (:=, i) and (:=,r).
Write a syntax directed translation scheme to convert expression and assignment strings into the post-fix form. You may assume that the name and type of a variable can be obtained by making the function calls 'give-type (id)' and 'give-name (id)' respectively.
A | Theory Explanation. |
Question 20 |
Consider the following program fragment in Pascal:
Program Main;
var X : integer;
procedure A:
var Y : integer;
procedure B:
var Z : integer;
procedure C:
var Z : integer;
begin(* Procedure C *)
:
end(* Procedure C *)
begin(*Procedure B*)
:
C; (* call to C *)
A; (* call to A *)
:
end(*Procedure B*)
begin(* Procedure A *)
:
B; (* call to B *)
:
end(* Procedure A *)
begin (* Main *)
:
A; (* call to A *)
:
end(* Main *) Assume that there are no calls to any procedures other than the ones indicated above. It is known that at some point of time during the execution of this program five activation records exist on the run-time stack. Describe the run-time stack at this point of time by clearly indicating the following: the top of the stack, the contents of the static link and dynamic link, and allocation of the local variables in each record.
A | Theory Explanation. |
Question 21 |
Following is a state table for some finite state machine.

(a) Find the equivalence partition on the states of the machine.
(b) Give the state table for the minimal machine. (Use appropriate names for the equivalent states. For example if states X and Y are equivalent then use XY as the name for the equivalent state in the minimal machine.)
A | Theory Explanation. |
Question 22 |
Let f = (w'+y)(x'+y)(w+x'+z)(w'+z)(x'+z)
(a) Express f as the minimal sum of products. Write only the answer.
(b) If the output line is stuck at 0, for how many input combinations will the value of f be incorrect?
A | Theory Explanation. |
Question 23 |
Following floating point number format is given
f is a fraction represented by a 6-bit mantissa (includes sign bit) in sign magnitude form e is a 4-bit exponent (includes sign hit) in sign magnitude form n = (f,e) = f, 2e is a floating point number.
Let A = 54.75 in decimal and
B = 9.75 in decimal.
(a) Represent A and B as floating point numbers in the above format.
(b) Show the steps involved in floating point addition of A and B.
(c) What is the percentage error (upto one position beyond decimal point) in the addition operation in (b)?
A | Theory Explanation. |
Question 24 |
A concurrent system consists of 3 processes using a shared resource R in a non-preemptible and mutually exclusive manner. The processes have unique priorities in the range 1.....3, 3 being the highest priority. It is required to synchronize the processes such that the resource is always allocated to the highest priority requester. The pseudo code for the system is as follows.
Shared Data
mutex:semaphore = 1:/* initialized to 1*/
process[3]:semaphore = 0; /*all initialized to 0 */
R_requested [3]:boolean = false; /*all initialized to false */
busy: boolean = false; /*initialized to false */
Code for processes
begin process
my-priority:integer;
my-priority:=____; /*in the range 1...3*/
repeat
request_R(my-priority);
P (proceed [my-priority]);
{use shared resource R}
release_R (my-priority);
forever
end process;
Procedures
procedure request_R(priority);
P(mutex);
if busy = true then
R_requested [priority]:=true;
else
begin
V(proceed [priority]);
busy:=true;
end
V(mutex); Give the pseudo code for the procedure release_R.
A | Theory Explanation. |
Question 25 |
A program P reads and processes 1000 consecutive records from a sequential file F stored on device D without using any file system facilities. Given the following
Size of each record = 3200 bytes Access time of D = 10 msecs Data transfer rate of D = 800 × 103 bytes/second CPU time to process each record = 3 msecs
What is the elapsed time of P if
(a) F contains unblocked records and P does not use buffering?
(b) F contains unblocked records and P uses one buffer (i.e., it always reads ahead into the buffer)?
(c) records of F are organized using a blocking factor of 2 (i.e., each block on D contains two records of F) and P uses one buffer?
You may assume that the CPU time needed to transfer a record from a buffer to a local variable of P is negligible.
A | Theory Explanation. |
Question 26 |
An operating system handles requests to resources as follows.
A process (which asks for some resources, uses them for some time and then exits the system) is assigned a unique timestamp are when it starts. The timestamps are monotonically increasing with time. Let us denote the timestamp of a process P by TS(P).
When a process P requests for a resource the OS does the following:
(i) If no other process is currently holding the resource, the OS awards the resource to P.
(ii) If some process Q with TS(Q) < TS(P) is holding the resource, the OS makes P wait for the resources.
(iii) If some process Q with TS(Q) > TS(P) is holding the resource, the OS restarts Q and awards the resources to P.
(Restarting means taking back the resources held by a process, killing it and starting it again with the same timestamp)
When a process releases a resource, the process with the smallest timestamp (if any) amongst those waiting for the resource is awarded the resource.
(a) Can a deadlock ever arise? If yes, show how. If not, prove it.
(b) Can a process P ever starve? If yes, show how. If not, prove it.
A | Theory Explanation. |
Question 27 |
Consider the following relational database schema:
EMP (eno name, age)
PROJ (pno name)
INVOLVED (eno, pno) EMP contains information about employees. PROJ about projects and INVOLVED about which employees involved in which projects. The underlined attributes are the primary keys for the respective relations.
(a) What is the relational algebra expression containing one or more of {σ,π,x,u,−} which is equivalent to SQL query.
select eno from EMP, INVOLVED where EMP.eno=INVOLVED.eno and INVOLVED.pno=3
(b) State in English (in not more than 15 words).
What the following relational algebra expressions are designed to determine
(i) πeno(INVOLVED) − πeno((πeno(INVOLVED) X πpno(PROJ))−INVOLVED)
(ii) πage(EMP) − πEage
(Note: ρE(EMP) conceptually makes a copy of EMP and names it K (ρ is called the rename operator))
A | Theory Explanation. |
Question 28 |
And since every attribute is key so the decomposed relation will be in BCNF and hence in 3NF.
Question 29 |
Now since all the attributes are keys, so R1 ∩ R2 will be a key of the decomposed relation.
And since every attribute is key so the decomposed relation will be in BCNF and hence in 3NF.
Question 30 |
Given the following algorithm for sorting an array X of N numbers:
SUBROUTINE SORT(X,N)
IF(N < 2)
RETURN
FOR(i=2 TO N INCREMENT BY 1)
FOR(j=1 TO i INCREMENT BY 1)
IF (X[i] > X[j])
CONTINUE
TEMP X[i]
X[i] = X[j]
X[j] = TEMP
END FOR
END FOR
END SUBROUTINE A good approximation of Halstead's estimated program length is
A | 20 |
B | 50 |
C | 80 |
D | 110 |
Question 31 |
Find if the following statements in the context of software testing are TRUE or FALSE.
(S1) Statement coverage cannot guarantee execution of loops in a program under test.
(S2) Use of independent path testing criterion guarantees execution of each loop in a program under test more than once.
A | True, True |
B | True, False |
C | False, True |
D | False, False |
Question 32 |
Which of the following requirement specifications can be validated?
- (S1) If the system fails during any operation, there should not be any loss of data
(S2) The system must provide reasonable performance even under maximum load conditions
(S3) The software executable must be deployable under MS Windows 95, 2000 and XP
(S4) User interface windows must fit on a standard monitor's screen
A | S4 and S3 |
B | S4 and S2 |
C | S3 and S1 |
D | S2 and S1 |
Question 33 |
R) False. We can give counter example. Let G has 5 vertices and 9 edges which is planar graph. Assume degree of one vertex is 2 and of all others are 4. Now, L(G) has 9 vertices (because G has 9 edges) and 25 edges. But for a graph to be planar,
|E| ≤ 3|v| - 6
For 9 vertices |E| ≤ 3 × 9 - 6
⇒ |E| ≤ 27 - 6
⇒ |E| ≤ 21. But L(G) has 25 edges and so is not planar.
As (R) is false, option (B) & (C) are eliminated.
Question 34 |
Which one of the following is NOT logically equivalent to ¬∃x(∀y(α) ∧ ∀z(β))?
A | ∀x(∃z(¬β)→∀y(α)) |
B | ∀x(∀z(β)→∃y(¬α)) |
C | ∀x(∀y(α)→∃z(¬β)) |
D | ∀x(∃y(¬α)→∃z(¬β)) |
∀x(∃z(¬β) → ∀y(α))
⇒ ∀x(¬∃z(¬β) ∨ ∀y(α))
⇒ ∀x(∀z(β)∨y(α))
⇒ ¬∃x¬(∀z(β)∨∀y(α))
⇒ ¬∃x(¬∀z(β)∧¬∀y(α))
A is Not equivalent to the given.
Option B:
∀x(∀z(β)→∃y(¬α))
⇒ ∀x(¬∀z(β)∨∃y(¬α))
⇒ ¬∃x¬(¬∀z(β)∨∃y(¬α))
⇒ ¬∃x(∀z(β)∨∀y(α))
B is Matching and equivalent to given.
Option C:
∀x(∀y(α)→∃z(¬β))
⇒ ∀x(¬∀y(α)∨∃z(¬β))
⇒ ¬∃x¬(¬∀y(α)∨∃z(¬β))
⇒ ¬∃x(∀y(α)∧z(β))
C is equivalent to the given.
Option D:
∀x(∃y(¬α)→∃z(¬β))
⇒ ∀x(¬∃y(¬α)∨∃z(β))
⇒ ∀x(∀y(α)∨∃z(β))
⇒ ¬∃x¬(∀y(α)∨∃z(β))
⇒ ¬∃x(¬∀y(α)∧¬∃z(β))
⇒ ¬∃x(¬∀y(α)∧∀z(¬β))
So D is Not equivalent to the given.
Question 35 |
A | 18.6 |
B | 27.9 |
C | 9.3 |
D | None of the above |
Each frame has a chance of 80% undamage which is 0.8 of getting through, the chance of the whole message getting through is (0.8)10, which is about 0.107. Call this value p.
The expected number of transmissions for an entire message is then

Now use a = 1-p to get E = 1/p. Thus, it takes an average of 1/0.107, or about 9.3 transmissions.
Question 36 |
A | 10000 bytes |
B | 100000 bits
|
C | 1250 bits |
D | None of the above |

Question 37 |
A | NL - 4, DLL - 4 |
B | NL - 4, DLL - 3 |
C | NL - 4, DLL - 6 |
D | NL - 2, DLL - 6 |
Question 38 |
A | port |
B | physical |
C | IP |
D | None |
Question 39 |
A | ensure that the line remains unbalanced |
B | have more than one symbol per bit period |
C | increase the bandwidth of a signal transmitted on the medium |
D | ensure that a transition occurs in the center of each bit period |
Question 40 |
A | require different amount of time |
B | require about the same amount of time |
C | require different amount of time with time difference between any two tasks being same |
D | require different amount with time difference between any two tasks being different |
Consider 4 stages in pipeline P1, P2, P3, P4, with each stage requires 1ns.
For large no. of instructions the time taken by pipeline to execute one task is 1ns.
But for non pipeline the time taken to execute one task is,
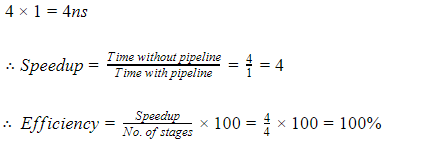
Case 2:
Now let’s consider 4 stages pipeline P1, P2, P3, P4, with each stage requiring 1ns, 2ns, 3ns, 4ns.
For large no. of instruction the time taken by pipeline to execute one task is max(1, 2, 3, 4)ns = 4ns
But for non pipeline the time taken to execute one task is,
1 + 2 + 3 + 4 = 10ns
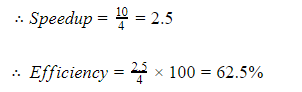
Hence from above it can be clearly seen that the concept of pipelining is most effective in improving performance if the tasks being performed in different stages require about the same amount of time.
Question 41 |
A | 2 |
B | 8 |
C | 10 |
D | None of the above |

Question 42 |
A | AND, OR
|
B | NOR |
C | NAND |
D | AND, OR, NOT |
Hence Option (a) set in not functionally complete.
Question 43 |
A | 10 |
B | 12 |
C | 13 |
D | 18.5 |
= 0.7 × 5ns + 0.3 × 50ns
= 3.5ns + 15ns
= 18.5 ns
Question 44 |
The number of min-terms after minimizing the following Boolean expression is
[D’ + AB’ + A’C + AC’D + A’C’D]’
A | 1 |
B | 46 |
C | 56 |
D | 76 |
(D’ + A’C’D + AB’ + A’C + AC’D)’
((D’ + D) (D’ + A’C’) + AB’ + A’C + AC’D)’
(D’ + A’C’ + AB’ + A’C + AC’D)’
(D’ + AC’D + AB’ + A’(C + C’))’
(D’ + AC’ + AB’ + A’)
(D’ + AC’ + (B’ + A’) (A + A’)
(D’ + AC’ + B’ + A’)
(D’ + (A + A’) (C’ + A’) + B’)’
(D’ + C’ + A’ + B’)’ = ABCD
Question 45 |
The speed up of a pipeline processing over an equivalent non-pipeline processing is defined by the ratio:
where n→no. of tasks, Tn→time of completion of each task, k→no. of segments of pipeline, Tp→clock cycle time, S→speed up ratio.
A | S = n Tn/ (k + n - 1) Tp |
B | S = n Tn/ (k + n + 1) Tp |
C | S = n Tn/ (k - n + 1) Tp |
D | S = (k + n - 1) Tp/ n Tn |
ET pipeline = k + n – 1 cycles
= (k + n – 1) Tp
In the same case, for a non-pipelined processor, execution time of ‘n’ instructions will be:
ETnon-pipeline = n * k * Tp
but in question k * Tp = Tn
Hence ETnon-pipeline = n * Tn
So, speedup (S) of the pipelined processor over non-pipelined processor, when ‘n’ tasks are executed on the same processor is:
S = Performance of pipelined processor /
Performance of Non-pipelined processor
As the performance of a processor is inversely proportional to the execution time, we have,
S = ETnon-pipeline / ETpipeline
=> S = [n *Tn] / [(k + n – 1) * Tp]
Question 46 |
A | 78% |
B | 91% |
C | 98% |
D | 80% |
Question 47 |
A | 0.0006 |
B | 0.00006 |
C | 0.006 |
D | None of the above |
Then (1 − p) is the probability that a memory access costs 100 nsec.
The probability that a page fault costs 20 msec is 0.7 ∗ p and the probability that a page fault costs 8 msec is 0.3 ∗ p.
Since 1 nsec = 1000000 msec, (1 − p) ∗ 100 + 0.7 ∗ p ∗ 20000000 + 0.3 ∗ p ∗ 8000000 = 200 (14000000 + 2400000 − 100)p = 100 p = 100/(16400100) = 6.1 ∗ 10^−6 = .0000061 = .00061%
Question 48 |
Which of the following scheduling algorithms could result in starvation?
i) First-come, first-served
ii) Shortest job first
iii) Round robin
iv) Priority
A | ii and iv |
B | i and iii |
C | iv only |
D | None of the above |
In priority scheduling algorithm the job with lowest priority may starve if the process with highest priority keeps coming.
FCFS and round robin scheduling algorithm will never cause starvation.
Question 49 |
A | A part of an operating system |
B | A specific memory location |
C | A single contiguous memory that was used in the olden days for running large program by swapping |
D | Overloading the system with many user files |
Question 50 |
A | Single level directory |
B | Two level directory |
C | Tree structured directory |
D | Acyclic graph directory |
