LPP
Question 1 |
Consider the following linear programming problem :
Max. z = 0.50 x2 – 0.10x1
Subject to the constraints
2x1 + 5x2 < 80
x1 + x2 < 20
and x1, x2 > 0
The total maximum profit (z) for the above problem is :
Max. z = 0.50 x2 – 0.10x1
Subject to the constraints
2x1 + 5x2 < 80
x1 + x2 < 20
and x1, x2 > 0
The total maximum profit (z) for the above problem is :
A | 6 |
B | 8 |
C | 101 |
D | 12 |
Question 2 |
Consider the following statements :
(a) If primal (dual) problem has a finite optimal solution, then its dual (primal) problem has a finite optimal solution.
(b) If primal (dual) problem has an unbounded optimal solution, then its dual (primal) has no feasible solution at all.
(c) Both primal and dual problems may be infeasible.
Which of the following is correct ?
(a) If primal (dual) problem has a finite optimal solution, then its dual (primal) problem has a finite optimal solution.
(b) If primal (dual) problem has an unbounded optimal solution, then its dual (primal) has no feasible solution at all.
(c) Both primal and dual problems may be infeasible.
Which of the following is correct ?
A | (a) and (b) only |
B | (a) and (c) only |
C | (b) and (c) only |
D | (a), (b) and (c)
|
Question 3 |
Consider the following statements :
(a) Assignment problem can be used to minimize the cost.
(b) Assignment problem is a special case of transportation problem.
(c) Assignment problem requires that only one activity be assigned to each resource.
Which of the following options is correct ?
(a) Assignment problem can be used to minimize the cost.
(b) Assignment problem is a special case of transportation problem.
(c) Assignment problem requires that only one activity be assigned to each resource.
Which of the following options is correct ?
A | (a) and (b) only |
B | (a) and (c) only |
C | (b) and (c) only |
D | (a), (b) and (c) |
Question 4 |
Consider the following linear programming (LP):
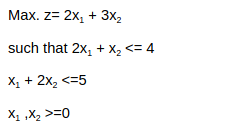
The optimum value of the LP is
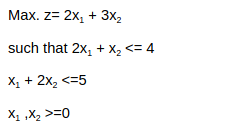
The optimum value of the LP is
A | 23 |
B | 9.5 |
C | 13 |
D | 8 |
Question 5 |
A linear programming problem (LPP) is as follows:
Min z=30x-18y, subject to the constraints; 3x+4y ≤ 60, 5x - 3y ≥ 20 and x,y ≥ 0. In this feasible region, the solution of LPP is/are
A.(4, 0)
B.(2,0)
C.(7, 5)
D.(0, 15)
E.(8,5)
Choose the correct answer from the options given below:
Min z=30x-18y, subject to the constraints; 3x+4y ≤ 60, 5x - 3y ≥ 20 and x,y ≥ 0. In this feasible region, the solution of LPP is/are
A.(4, 0)
B.(2,0)
C.(7, 5)
D.(0, 15)
E.(8,5)
Choose the correct answer from the options given below:
A | A and C only
|
B | B only |
C | E only |
D | D only |
Question 6 |
Consider the primal problem:
Maximize z=5x1+12x2+4x3
Subject to x1+2x2+x3=10
2x1-x2+3x3=8
x1,x2,x3>=0
its dual problem is
Minimize w=10y1+8y2
Subject to y1+2y2>=5
2y1-y2>=12
y1+3y2>=4
Which of the following is correct?
Maximize z=5x1+12x2+4x3
Subject to x1+2x2+x3=10
2x1-x2+3x3=8
x1,x2,x3>=0
its dual problem is
Minimize w=10y1+8y2
Subject to y1+2y2>=5
2y1-y2>=12
y1+3y2>=4
Which of the following is correct?
A | y1>=0, y2 unrestricted
|
B | y1>=0,y2>=0
|
C | y1 is unrestricted,y2>=0
|
D | y1 is unrestricted,y2 restricted |
Question 7 |
If an artificial variable is present in the ‘basic variable’ column of optimal simplex table, then the solution is
A | Optimum |
B | Infeasible |
C | Unbounded |
D | Degenerate |
Question 8 |
The occurrence of degeneracy while solving a transportation problem means that
A | total supply equals total demand |
B | total supply does not equal total demand |
C | the solution so obtained is not feasible |
D | none of these |
Question 8 Explanation:
The occurrence of degeneracy while solving a transportation problem means that the solution so obtained is not feasible.
Question 9 |
Five men are available to do five different jobs. From past records, the time (in hours) that each man takes to do each job is known and is given in the following table :
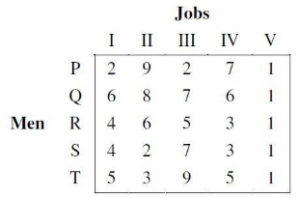
Find out the minimum time required to complete all the jobs.

Find out the minimum time required to complete all the jobs.
A | 5 |
B | 11 |
C | 13 |
D | 15 |
Question 10 |
Consider the following statements with respect to duality in LPP:
(a) The final simplex table giving optimal solution of the primal also contains optimal solution of its dual in itself.
(b) If either the primal or the dual problem has a finite optimal solution, then the other problem also has a finite optimal solution.
(c) If either problem has an unbounded optimal solution, then the other problem has no feasible solution at all. Which of the statements is (are) correct?
A | only (a) and (b) |
B | only (a) and (c) |
C | only (b) and (c) |
D | (a), (b) and (c) |
Question 10 Explanation:
Duality in LPP:
TRUE: The final simplex table giving optimal solution of the primal also contains optimal solution of its dual in itself.
TRUE: If either the primal or the dual problem has a finite optimal solution, then the other problem also has a finite optimal solution.
TRUE: If either problem has an unbounded optimal solution, then the other problem has no feasible solution at all.
TRUE: The final simplex table giving optimal solution of the primal also contains optimal solution of its dual in itself.
TRUE: If either the primal or the dual problem has a finite optimal solution, then the other problem also has a finite optimal solution.
TRUE: If either problem has an unbounded optimal solution, then the other problem has no feasible solution at all.
Question 11 |
A basic feasible solution of an mXn Transportation-Problem is said to be non-degenerate, if basic feasible solution contains exactly____number of individual allocation in ___positions
A | m+n+1, independent |
B | m+n-1, independent |
C | m+n-1, appropriate |
D | m-n+1, independent |
Question 11 Explanation:
The initial solution of a transportation problem is said to be non-degenerate basic feasible solution if it satisfies:
→The solution must be feasible, i.e. it must satisfy all the supply and demand constraints.
→The number of positive allocations must be equal to m+n-1, where m is the number of rows and n is the number of columns.
→All the positive allocations must be in independent positions
A few terms used in connection with transportation models are defined below.
1. Feasible solution: A feasible solution to a transportation problem is a set of non-negative allocations, xij that satisfies the rim (row and column) restrictions.
2. Basic feasible solution: A feasible solution to a transportation problem is said to be a basic feasible solution if it contains no more than m + n – 1 non – negative allocations, where m is the number of rows and n is the number of columns of the transportation problem.
3. Optimal solution: A feasible solution (not necessarily basic) that minimizes (maximizes) the transportation cost (profit) is called an optimal solution.
4. Non-degenerate basic feasible solution: A basic feasible solution to a (m x n) transportation problem is said to be non – degenerate if, the total number of non-negative allocations is exactly m + n – 1 (i.e., number of independent constraint equations), and these m + n – 1 allocations are in independent positions.
5. Degenerate basic feasible solution: A basic feasible solution in which the total number of non-negative allocations is less than m + n – 1 is called degenerate basic feasible solution.
Note: It is very standard and regular question and asked in UGC-NET Dec-2015 paper-3
Ref-https://solutionsadda.in/ugc-net-cs-2015-dec-paper-3/
→The solution must be feasible, i.e. it must satisfy all the supply and demand constraints.
→The number of positive allocations must be equal to m+n-1, where m is the number of rows and n is the number of columns.
→All the positive allocations must be in independent positions
A few terms used in connection with transportation models are defined below.
1. Feasible solution: A feasible solution to a transportation problem is a set of non-negative allocations, xij that satisfies the rim (row and column) restrictions.
2. Basic feasible solution: A feasible solution to a transportation problem is said to be a basic feasible solution if it contains no more than m + n – 1 non – negative allocations, where m is the number of rows and n is the number of columns of the transportation problem.
3. Optimal solution: A feasible solution (not necessarily basic) that minimizes (maximizes) the transportation cost (profit) is called an optimal solution.
4. Non-degenerate basic feasible solution: A basic feasible solution to a (m x n) transportation problem is said to be non – degenerate if, the total number of non-negative allocations is exactly m + n – 1 (i.e., number of independent constraint equations), and these m + n – 1 allocations are in independent positions.
5. Degenerate basic feasible solution: A basic feasible solution in which the total number of non-negative allocations is less than m + n – 1 is called degenerate basic feasible solution.
Note: It is very standard and regular question and asked in UGC-NET Dec-2015 paper-3
Ref-https://solutionsadda.in/ugc-net-cs-2015-dec-paper-3/
Question 12 |
In the Hungarian method for solving assignment problem, an optimal assignment requires that the maximum number of lines that can be drawn through squares with zero opportunity cost is equal to the number of:
A | rows or columns |
B | rows + columns |
C | rows + columns - 1 |
D | rows + columns + 1 |
Question 12 Explanation:
In the Hungarian method for solving assignment problem, an optimal assignment requires that the maximum number of lines that can be drawn through squares with zero opportunity cost is equal to the number of rows or columns.
Question 13 |
Consider the following transportation problem:


A | is degenerate solution |
B | is optimum solution |
C | needs to improve |
D | is infeasible solution |
Question 13 Explanation:
Step1: In vogel’s approximation method first find out the row difference(by calculating the difference between the two smallest values of that row) and column difference(by calculating the difference between the two smallest values of that row)
Then select the row having highest row difference and after selecting row choose the column/cell of that row having minimum value.
After that fulfill the demand by using supply from the selected row and column.
After that if demand becomes zero then delete that column and if the row become zero then delete that row and then repeat step 1.
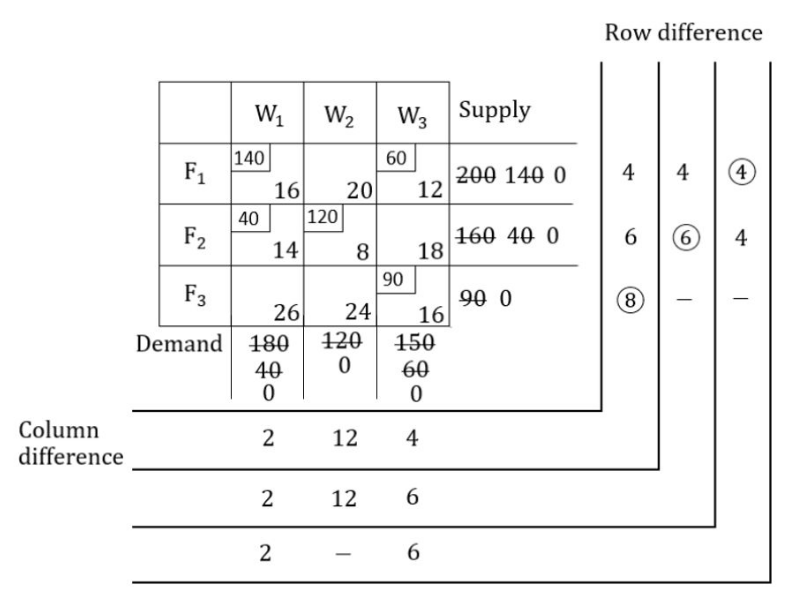
Then select the row having highest row difference and after selecting row choose the column/cell of that row having minimum value.
After that fulfill the demand by using supply from the selected row and column.
After that if demand becomes zero then delete that column and if the row become zero then delete that row and then repeat step 1.

Question 14 |
Given the following statements with respect to linear programming problem:
S 1 : The dual of the dual linear programming problem is again the primal problem
S 2 : If either the primal or the dual problem has an unbounded objective function value, the other problem has no feasible solution.
S 3 : If either the primal or dual problem has a finite optimal solution, the other one also possesses the same, and the optimal value of the objective functions of the two problems are equal.
Which of the following is true?
S 1 : The dual of the dual linear programming problem is again the primal problem
S 2 : If either the primal or the dual problem has an unbounded objective function value, the other problem has no feasible solution.
S 3 : If either the primal or dual problem has a finite optimal solution, the other one also possesses the same, and the optimal value of the objective functions of the two problems are equal.
Which of the following is true?
A | S 1 and S 2 |
B | S 1 and S 3 |
C | S 2 and S 3 |
D | S 1 , S 2 and S 3 |
Question 14 Explanation:
S 1 : TRUE: The dual of the dual linear programming problem is again the primal problem
S 2 : TRUE: If either the primal or the dual problem has an unbounded objective function value, the other problem has no feasible solution.
S 3 : TRUE: If either the primal or dual problem has a finite optimal solution, the other one also possesses the same, and the optimal value of the objective functions of the two problems are equal.
S 2 : TRUE: If either the primal or the dual problem has an unbounded objective function value, the other problem has no feasible solution.
S 3 : TRUE: If either the primal or dual problem has a finite optimal solution, the other one also possesses the same, and the optimal value of the objective functions of the two problems are equal.
Question 15 |
In constraint satisfaction problem, constraints can be stated as __________.
A | Arithmetic equations and inequalities that bind the values of variables |
B | Arithmetic equations and inequalities that doesn’t bind any restriction over variables |
C | Arithmetic equations that impose restrictions over variables
|
D | Arithmetic equations that discard constraints over the given variables |
Question 16 |
A basic feasible solution of a linear programming problem is said to be __________ if at least one of the basic variables is zero.
A | degenerate |
B | non-degenerate |
C | infeasible |
D | unbounded |
Question 16 Explanation:
Feasible Solution: The set of values of decision variables Xj (j = 1, 2, ... n) which satisfy all the constraints and non-negativity conditions of a linear programming problem simultaneously is said to constitute the feasible solution to that problem.
Basic Solution: For a set of m simultaneous equations in n variables (n > m), a solution obtained by setting (n – m) variables equal to zero and solving for remaining m variables is called a “basic feasible solution”.
Basic Feasible Solution: A feasible solution to LP problem which is also the basic solution is called the “basic feasible solution”. Basic feasible solutions are of two types;
(a) Degenerate: A basic feasible solution is called degenerate if value of at least one basic variable is zero.
(b) Non-degenerate: A basic feasible solution is called ‘non-degenerate’ if all values of m basic variables are non-zero and positive.
Hence the correct option is option(A)
Basic Solution: For a set of m simultaneous equations in n variables (n > m), a solution obtained by setting (n – m) variables equal to zero and solving for remaining m variables is called a “basic feasible solution”.
Basic Feasible Solution: A feasible solution to LP problem which is also the basic solution is called the “basic feasible solution”. Basic feasible solutions are of two types;
(a) Degenerate: A basic feasible solution is called degenerate if value of at least one basic variable is zero.
(b) Non-degenerate: A basic feasible solution is called ‘non-degenerate’ if all values of m basic variables are non-zero and positive.
Hence the correct option is option(A)
Question 17 |
Consider the following conditions:
(a)The solution must be feasible, i.e. it must satisfy all the supply and demand constraints.
(b)The number of positive allocations must be equal to m+n-1, where m is the number of rows and n is the number of columns.
(c)All the positive allocations must be in independent positions.
The initial solution of a transportation problem is said to be non-degenerate basic feasible solution if it satisfies:
(a)The solution must be feasible, i.e. it must satisfy all the supply and demand constraints.
(b)The number of positive allocations must be equal to m+n-1, where m is the number of rows and n is the number of columns.
(c)All the positive allocations must be in independent positions.
The initial solution of a transportation problem is said to be non-degenerate basic feasible solution if it satisfies:
A | (a) and (b) only |
B | (a) and (c) only |
C | (b) and (c) only |
D | (a), (b) and (c)
|
Question 17 Explanation:
The initial solution of a transportation problem is said to be non-degenerate basic feasible solution if it satisfies:
→The solution must be feasible, i.e. it must satisfy all the supply and demand constraints.
→The number of positive allocations must be equal to m+n-1, where m is the number of rows and n is the number of columns.
→All the positive allocations must be in independent positions.
→The solution must be feasible, i.e. it must satisfy all the supply and demand constraints.
→The number of positive allocations must be equal to m+n-1, where m is the number of rows and n is the number of columns.
→All the positive allocations must be in independent positions.
Question 18 |
Consider the following transportation problem:

The transportation cost in the initial basic feasible solution of the above transportation problem using Vogel’s Approximation method is:

The transportation cost in the initial basic feasible solution of the above transportation problem using Vogel’s Approximation method is:
A | 1450 |
B | 1465 |
C | 1480 |
D | 1520 |
Question 19 |
The region of feasible solution of a linear programming problem has a _____ property in geometry, provided the feasible solution of the problem exists.
A | concavity |
B | convexity |
C | quadratic |
D | polyhedron |
Question 19 Explanation:
→ The region of feasible solution of an LP problem has a convexity property in geometry, provided the feasible solution of the problem exists.
→ The basic feasible solutions for a standard form LP are vertices for the convex set of feasible solution for the LP.
→ If an LP has a finite optimal objective function value, then the optimal value occurs at at least one basic feasible solution.
→ The basic feasible solutions for a standard form LP are vertices for the convex set of feasible solution for the LP.
→ If an LP has a finite optimal objective function value, then the optimal value occurs at at least one basic feasible solution.
Question 20 |
Consider the following statements:
(a) Revised simplex method requires lesser computations than the simplex method.
(b) Revised simplex method automatically generates the inverse of the current basis matrix.
(c) Less number of entries are needed in each table of revised simplex method than usual simplex method.
Which of these statements are correct?
(a) Revised simplex method requires lesser computations than the simplex method.
(b) Revised simplex method automatically generates the inverse of the current basis matrix.
(c) Less number of entries are needed in each table of revised simplex method than usual simplex method.
Which of these statements are correct?
A | (a) and (b) only |
B | (a) and (c) only |
C | (b) and (c) only |
D | (a), (b) and (c) |
Question 21 |
The following transportation problem: is


A | infeasible solution |
B | optimum solution |
C | non-optimum solution |
D | unbounded solution |
Question 22 |
Which of the following statements is false about convex minimization problem ?
A | If a local minimum exists, then it is a global minimum |
B | The set of all global minima is convex set |
C | The set of all global minima is concave set |
D | For each strictly convex function, if the function has a minimum, then the minimum is unique |
Question 22 Explanation:
Properties of convex optimization problems:
1. Every local minimum is a global minimum
2. The optimal set is convex
3. If the objective function is strictly convex, then the problem has at most one optimal point.
These results are used by the theory of convex minimization along with geometric notions from functional analysis (in Hilbert spaces) such as the Hilbert projection theorem, the separating hyperplane theorem, and Farkas' lemma.
1. Every local minimum is a global minimum
2. The optimal set is convex
3. If the objective function is strictly convex, then the problem has at most one optimal point.
These results are used by the theory of convex minimization along with geometric notions from functional analysis (in Hilbert spaces) such as the Hilbert projection theorem, the separating hyperplane theorem, and Farkas' lemma.
Question 23 |
__________ model is designed to bring prices down by increasing the number of customers who buy a particular product at once.
A | Economic Order Quantity |
B | Inventory |
C | Data Mining |
D | Demand-Sensitive Pricing |
Question 23 Explanation:
→ Demand-Sensitive Pricing model is designed to bring prices down by increasing the number of customers who buy a particular product at once.
→ Demand sensitivity is referred to the change in demand for a product when its price is changed by a small amount.
Price Elasticity of demand = ((%change in quantity demanded) / (% change in price of a particular product))
→ Demand sensitivity is referred to the change in demand for a product when its price is changed by a small amount.
Price Elasticity of demand = ((%change in quantity demanded) / (% change in price of a particular product))
Question 24 |
Which of the following statements is true?
A | The sentence S is a logical consequence of S1,.., Sn if and only if S1 ∧ S2 ∧.... ∧ Sn → S is satisfiable. |
B | The sentence S is a logical consequence of S1,..., Sn if and only if S1 ∧ S2 ∧........ ∧Sn → S is valid. |
C | The sentence S is a logical consequence of S1,..., Sn if and only if S1 ∧ S2 ∧........ ∧ Sn ∧ S is consistent. |
D | The sentence S is a logical consequence of S1,..., Sn if and only if S1 ∧ S2 ∧........ ∧ Sn ∧ S is inconsistent. |
Question 25 |
A t-error correcting q-nary linear code must satisfy:

Where M is the number of code words and X is

Where M is the number of code words and X is
A | qn |
B | qt |
C | q-n |
D | q-t |
Question 26 |
With respect to a loop in the transportation table, which one of the following is not correct?
A | Every loop has an odd no. of cells and at least 5. |
B | Closed loops may or may not be square in shape. |
C | All the cells in the loop that have a plus or minus sign, except the starting cell, must be occupied cells. |
D | Every loop has an even no. of cells and at least four. |
Question 27 |
At which of the following stage(s), the degeneracy do not occur in transportation problem ? (m, n represents number of sources and destinations respectively)
(a) While the values of dual variables ui and vj cannot be computed.
(b) While obtaining an initial solution, we may have less than m + n – 1 allocations.
(c) At any stage while moving towards optimal solution, when two or more occupied cells with the same minimum allocation become unoccupied simultaneously.
(d) At a stage when the no. of +ve allocation is exactly m + n – 1.
(a) While the values of dual variables ui and vj cannot be computed.
(b) While obtaining an initial solution, we may have less than m + n – 1 allocations.
(c) At any stage while moving towards optimal solution, when two or more occupied cells with the same minimum allocation become unoccupied simultaneously.
(d) At a stage when the no. of +ve allocation is exactly m + n – 1.
A | (a), (b) and (c) |
B | (a), (c) and (d) |
C | (a) and (d) |
D | (a), (b), (c) and (d) |
Question 28 |
Consider the following LPP :
Min. Z = X1 + X2 + X3
Subject to 3X1 + 4X3 ≤ 5
5X1 + X2 + 6X3 = 7
8X1 + 9X3 ≥ 2,
X1, X2, X3 ≥ 0
The standard form of this LPP shall be :
Min. Z = X1 + X2 + X3
Subject to 3X1 + 4X3 ≤ 5
5X1 + X2 + 6X3 = 7
8X1 + 9X3 ≥ 2,
X1, X2, X3 ≥ 0
The standard form of this LPP shall be :
A |  |
B | 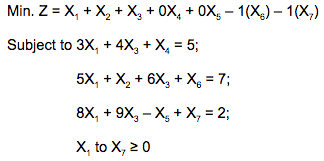 |
C | 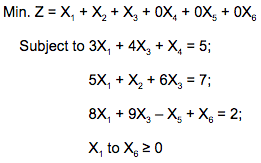 |
D |  |
Question 28 Explanation:

Question 29 |
Which of the following is a valid reason for causing degeneracy in a transportation problem ?
Here m is no. of rows and n is no. of columns in transportation table
Here m is no. of rows and n is no. of columns in transportation table
A | When the number of allocations is m+n−1. |
B | When two or more occupied cells become unoccupied simultaneously. |
C | When the number of allocations is less than m+n−1. |
D | When a loop cannot be drawn without using unoccupied cells, except the starting cell of the loop. |
Question 30 |
Consider the following LPP :
Max Z = 15x1 + 10x2
Subject to the constraints
4x1 + 6x2 ≤ 360
3x1 + 0x2 ≤ 180
0x1 + 5x2 ≤ 200
x1, x2 / 0
The solution of the LPP using Graphical solution technique is :
Max Z = 15x1 + 10x2
Subject to the constraints
4x1 + 6x2 ≤ 360
3x1 + 0x2 ≤ 180
0x1 + 5x2 ≤ 200
x1, x2 / 0
The solution of the LPP using Graphical solution technique is :
A | x1=60, x2=0 and Z=900 |
B | x1=60, x2=20 and Z=1100 |
C | x1=60, x2=30 and Z=1200 |
D | x1=50, x2=40 and Z=1150 |
Question 31 |
Consider the following LPP :
Min Z = 2x1 + x2 + 3x3
Subject to :
x1 − 2x2 + x3 ≥ 4
2x1 + x2 + x3 ≤ 8
x1 − x3 ≥ 0
x1, x2, x3 ≥ 0
The solution of this LPP using Dual Simplex Method is :
Min Z = 2x1 + x2 + 3x3
Subject to :
x1 − 2x2 + x3 ≥ 4
2x1 + x2 + x3 ≤ 8
x1 − x3 ≥ 0
x1, x2, x3 ≥ 0
The solution of this LPP using Dual Simplex Method is :
A | x1=0, x2=0, x3=3 and Z=9 |
B | x1=0, x2=6, x2=0 and Z=6 |
C | x1=4, x2=0, x2=0 and Z=8 |
D | x1=2, x2=0, x2=2 and Z=10 |
Access subject wise (1000+) question and answers by becoming as a solutions adda PRO SUBSCRIBER with Ad-Free content
Register Now
You have completed
questions
question
Your score is
Correct
Wrong
Partial-Credit
You have not finished your quiz. If you leave this page, your progress will be lost.
Correct Answer
You Selected
Not Attempted
Final Score on Quiz
Attempted Questions Correct
Attempted Questions Wrong
Questions Not Attempted
Total Questions on Quiz
Question Details
Results
Date
Score
Hint
Time allowed
minutes
seconds
Time used
Answer Choice(s) Selected
Question Text
Need more practice!
Keep trying!
Not bad!
Good work!
Perfect!
