Asymptotic-Complexity
Question 1 |
Consider the following two functions:
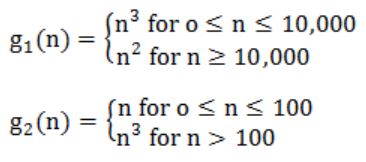
Which of the following is true?
g1(n) is O(g2(n)) | |
g1 (n) is O(3) | |
g2 (n) is O(g1 (n)) | |
g2 (n) is O(n) | |
Both A and B |
Growth rate of g1 is less than that of g2 i.e., g1(n) = O(g2(n)) = O(n).
Question 2 |
An array A contains n integers in locations A[0],A[1], …………… A[n-1]. It is required to shift the elements of the array cyclically to the left by K places, where 1≤K≤n-1. An incomplete algorithm for doing this in linear time, without using another is given below. Complete the algorithm by filling in the blanks. Assume all variables are suitably declared.
min:=n;
i=0;
while _____do
begin
temp:=A[i];
j:=i;
while _____do
begin
A[j]:=_____;
j:=(j+K) mod n;
if jTheory Explanation. |
Question 3 |
Consider the following recursive function:
function fib (1:integer);integer; begin if (n=0) or (n=1) then fib:=1 else fib:=fib(n-1) + fib(n-2) end;
The above function is run on a computer with a stack of 64 bytes. Assuming that only return address and parameter and passed on the stack, and that an integer value and an address takes 2 bytes each, estimate the maximum value of n for which the stack will not overflow. Give reasons for your answer.
Theory Explanation. |
Question 4 |
f ( n ^2 ) ( f ( n ) ^2 ), when f ( n ) is a polynomial | |
f ( n ^2 ) o ( f ( n ) ^2 ) | |
f ( n ^2 ) O ( f ( n ) ^2 ), when f ( n ) is an exponential function | |
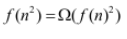 |
f(n)=n^c where c is a constant
f(n^2) = (n^2)^c = n^2c
(f(n))^2 = (n^c)^2 = n^2c
f(n^2) = (f(n))^2 is TRUE asymptotically.
Option-B: FALSE: The small omega function indicates the tightest upper bound.
f(n)^2 < o(f(n)^2) is FALSE asymptotically.
Option-C: FALSE: Consider f(n)=logn
f(n^2)=logn^2 = 2*logn
(f(n))^2 = (logn)^2 = logn * logn
f(n^2) <=Ω(f(n))^2 is FALSE asymptotically.
Option-D: FALSE:
Exponential values(Eg: 2^n, 3^n,..,k^n where k is a constant ”
f(n)=3^n
f(n^2)=f(3^(n^2)
(f(n))^2 = (3^n)^2 = 3^2n
f(n^2) >= O(f(n))^2 is FALSE asymptotically.
Question 5 |
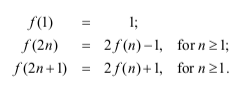
Then, which of the following statements is/are TRUE?
f (2^ n -1) 2^ n -1 | |
f (2 ^n ) 1 | |
f (5 . 2 ^n ) 2^ n + 1 1 | |
f (2^ n + 1) 2 ^n + 1 |
Based on the “n” value we can get Option-A, B and C are correct.
Question 6 |

Which one of the following options arranges the functions in the increasing order of asymptotic growth rate?
f2, f3, f1 | |
f3, f2, f1 | |
f2, f1, f3 | |
f1, f2, f3 |
The asymptotic notation order should be
Constant < logarithmic < linear < polynomial < exponential < factorial
F2 and F3 → Polynomial
F1 → Exponential
By the order of asymptotic notations F1 is definitely larger.
Method-1:
Consider n=100
F1 : 100 ^100 ⇒ 1.e+200
F2 : N^log(100) base 2 ⇒ 100 ^ log(100) base 2 ⇒ 100^6.6438561897747 = 1,93,96,00,91,15,564.181300016469223466
F3 : N^Sqrt(n) ====> 100^Sqrt(100) ⇒ 100^10 ⇒ 10,00,00,00,00,00,00,00,00,000
Method-2:
We can apply "log" on both sides.
log(F1)=nlog10 (base 2)
log(F2)=(logn)^2 = logn * logn (base 2)
log(F3)=sqrt(n)logn (base 2)
Answer: F2< F3< F1
Question 7 |
Consider the following functions from positives integers to real numbers
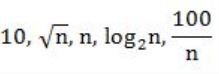
The CORRECT arrangement of the above functions in increasing order of asymptotic complexity is:
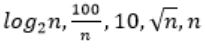 | |
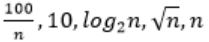 | |
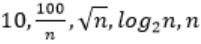 | |
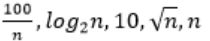 |
Step-1: Take n=2048 or 211 (Always take n is very big number)
Step-2: Divide functions into 2 ways
1. Polynomial functions
2. Exponential functions
Step-3: The above functions are belongs to polynomial. So, simply substitute the value of n,
First compare with constant values.
→ 100 / 2048 = 0.048828125
→ 10 > 100/ 2048
→ log2 2048 =11
→ √n = 45.25483399593904156165403917471
→ n = 2048
So, Option B is correct
Question 8 |
I. f(n) = O(g(n))
II. f(n) = Ω(g(n))
Only I | |
Only II | |
Both I and II | |
Neither I nor II |
Question 9 |
Which of the given options provides the increasing order of asymptotic complexity of functions f1, f2, f3 and f4?
f1(n)=2n f2(n)=n3/2 f3(n)=n log2 n f4(n)=nlog2n
f3, f2, f4, f1 | |
f3, f2, f1, f4 | |
f2, f3, f1, f4 | |
f2, f3, f4, f1 |
→ Divide functions into 2 categories
1. Polynomial functions
2. Exponential functions
Above 4 functions we have only one exponential function is f1 (n) = 2n . So, It’s value is higher than to rest of the functions.
Substitute log on both sides then we get an ascending order is f3, f2, f4.
Question 10 |
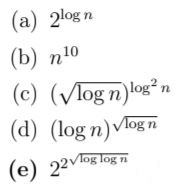
a | |
b | |
c | |
d | |
e |
