Binary-Trees
Question 1 |
What is the number of binary trees with 3 nodes which when traversed in postorder give the sequence A, B, C? Draw all these binary trees.
Theory Explanation. |
Question 2 |
The preorder traversal of a binary search tree is 15, 10, 12, 11, 20, 18, 16, 19.
Which one of the following is the postorder traversal of the tree?
20, 19, 18, 16, 15, 12, 11, 10 | |
11, 12, 10, 16, 19, 18, 20, 15
| |
10, 11, 12, 15, 16, 18, 19, 20 | |
19, 16, 18, 20, 11, 12, 10, 15 |
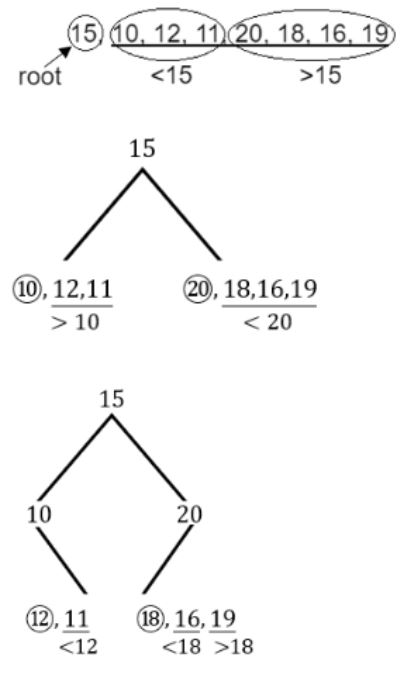

Postorder:
11, 12, 10, 16, 19, 18, 20, 15
Question 3 |
What is the worst case time complexity of inserting n2 elements into an AVL-tree with n elements initially?
θ(n4)
| |
θ(n2)
| |
θ(n3) | |
θ(n2 log n) |
In question they asked about n2 elements.
So, In worst case it will take o(n2 log n) time.
Question 4 |
In a balanced binary search tree with n elements, what is the worst case time complexity of reporting all elements in range [a,b]? Assume that the number of reported elements is k.
θ(n log k) | |
θ(log n + k) | |
θ(k log n) | |
θ(log n) |
Time complexity of the above program is O(h + k) where h is the height of BST and k is the number of nodes in a given range.
Here h is log n, hence O(log n+k).
Question 5 |
In the balanced binary tree in the below figure, how many nodes will become unbalanced when a node is inserted as a child of the node “g”?

1 | |
3 | |
7 | |
8 |
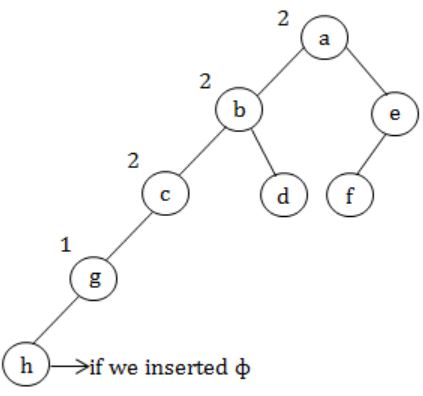
a, b, c are going to unbalance.
Question 6 |
Which of the following sequences denotes the post order traversal sequence of the tree of question 14?
f e g c d b a | |
g c b d a f e | |
g c d b f e a | |
f e d g c b a |
Left → Right → Root
g c d b f e a
Question 7 |
A binary search tree is generated by inserting in order the following integers:
50, 15, 62, 5, 20, 58, 91, 3, 8, 37, 60, 24
The number of nodes in the left subtree and right subtree of the root respectively is
(4, 7) | |
(7, 4) | |
(8, 3) | |
(3, 8) |
So greater than 50 will be in right subtree of 50 and less than 50 in left subtree.
So, answer will be (7, 4).
Question 8 |
A binary search tree contains the value 1, 2, 3, 4, 5, 6, 7, 8. The tree is traversed in pre-order and the values are printed out. Which of the following sequences is a valid output?
5 3 1 2 4 7 8 6 | |
5 3 1 2 6 4 8 7 | |
5 3 2 4 1 6 7 8 | |
5 3 1 2 4 7 6 8 |
Option D:
Let draw binary search tree for the given sequence,
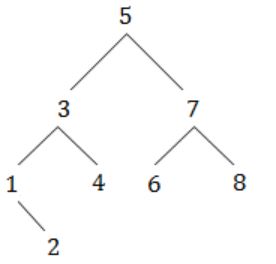
After traversing through this tree we will get same sequence.
Question 9 |
Which of the following statements is false?
A tree with a n nodes has (n – 1) edges | |
A labeled rooted binary tree can be uniquely constructed given its postorder and preorder traversal results | |
A complete binary tree with n internal nodes has (n + 1) leaves | |
Both B and C |
D: The maximum no. of nodes in a binary tree of height h is 2h+1 - 1.
h=2 ⇒ 23 - 1 ⇒ 7
Question 10 |
Draw the binary tree with node labels a, b, c, d, e, f and g for which the inorder and postorder traversals result in the following sequences:
Inorder a f b c d g e Postorder a f c g e d b
Theory Explanation. |
Question 11 |
Consider the following nested representation of binary trees: (X Y Z) indicates Y and Z are the left and right sub stress, respectively, of node X. Note that Y and Z may be NULL, or further nested. Which of the following represents a valid binary tree?
(1 2 (4 5 6 7)) | |
(1 (2 3 4) 5 6) 7) | |
(1 (2 3 4) (5 6 7)) | |
(1 (2 3 NULL) (4 5)) |

(Proper Representation)
Question 12 |
Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal. Respectively, of a complete binary tree. Which of the following is always tree?
LASTIN = LASTPOST | |
LASTIN = LASTPRE | |
LASTPRE = LASTPOST | |
None of the above |
But in case of complete binary last level need not to be full in that case LASTPRE is not equal to LASTIN.
Question 13 |
Draw all binary trees having exactly three nodes labeled A, B and C on which Preorder traversal gives the sequence C, B, A.
Theory Explanation is given below. |

Total 5 binary trees are possible with the preorder C, B, A.
Question 14 |
Consider the label sequences obtained by the following pairs of traversals on a labeled binary tree. Which of these pairs identify a tree uniquely?
(i) preorder and postorder (ii) inorder and postorder (iii) preorder and inorder (iv) level order and postorder
(i) only | |
(ii), (iii)
| |
(iii) only
| |
(iv) only |
(i) Inorder and Preorder
(ii) Inorder and Postorder
(iii) Inorder and Levelorder
→ And following are do not
(i) Post order and Preorder
(ii) Pre order and Level order
(iii) Post order and Level order
Question 15 |
Consider the following C program segment
struct CellNode
{
struct CelINode *leftchild;
int element;
struct CelINode *rightChild;
}
int Dosomething(struct CelINode *ptr)
{
int value = 0;
if (ptr != NULL)
{
if (ptr->leftChild != NULL)
value = 1 + DoSomething(ptr->leftChild);
if (ptr->rightChild != NULL)
value = max(value, 1 + DoSomething(ptr->rightChild));
}
return (value);
}
The value returned by the function DoSomething when a pointer to the root of a non-empty tree is passed as argument is
The number of leaf nodes in the tree | |
The number of nodes in the tree | |
The number of internal nodes in the tree | |
The height of the tree |
→ So given that pointer to root of tree is passed to DoSomething ( ), it will return height of the tree. It is done when the height of single node is '0'.
Question 16 |
A rooted tree with 12 nodes has its nodes numbered 1 to 12 in pre-order. When the tree is traversed in post-order, the nodes are visited in the order 3, 5, 4, 2, 7, 8, 6, 10, 11, 12, 9, 1.
Reconstruct the original tree from this information, that is, find the parent of each node, and show the tree diagrammatically.
Theory Explanation. |
Question 17 |
Prove by the principal of mathematical induction that for any binary tree, in which every non-leaf node has 2 descendants, the number of leaves in the tree is one more than the number of non-leaf nodes.
Theory Explanation. |
Question 18 |
An array of integers of size n can be converted into a heap by adjusting the heaps rooted at each internal node of the complete binary tree starting at the node ⌊(n - 1) /2⌋, and doing this adjustment up to the root node (root node is at index 0) in the order ⌊(n - 1)/2⌋, ⌊(n - 3)/2⌋, ....., 0. The time required to construct a heap in this manner is
O(log n) | |
O(n) | |
O(n log log n) | |
O(n log n) |
And we know that time complexity for building the heap is O(n).
Question 19 |
In a binary tree, the number of internal nodes of degree 1 is 5, and the number of internal nodes of degree 2 is 10. The number of leaf nodes in the binary tree is
10 | |
11 | |
12 | |
15 |
No. of 1 degree nodes = 5
No. of 2 degree nodes = 10
Total no. of edges = (1*5) + (2*10) = 5 + 20 = 25
So, Total no. of edges = 25 + 1 = 26 (No. of nodes in a tree is 1 more than no. of edges)
Total no. of leaf nodes (node with 0 degree) = 26 - 5 - 10 = 11
Question 20 |
Suppose that we have numbers between 1 and 100 in a binary search tree and want to search for the number 55. Which of the following sequences CANNOT be the sequence of nodes examined?
{10, 75, 64, 43, 60, 57, 55} | |
{90, 12, 68, 34, 62, 45, 55} | |
{9, 85, 47, 68, 43, 57, 55} | |
{79, 14, 72, 56, 16, 53, 55} |
Question 21 |
An array X of n distinct integers is interpreted as a complete binary tree. The index of the first element of the array is 0. The index of the parent of element X[i],i≠0 is?
⌊i/2⌋ | |
⌈(i-1)/2⌉ | |
⌈i/2⌉ | |
⌈i/2⌉ - 1 |
Question 22 |
An array X of n distinct integers is interpreted as a complete binary tree. The index of the first element of the array is 0. If only the root node does not satisfy the heap property, the algorithm to convert the complete binary tree into a heap has the best asymptotic time complexity of
O(n) | |
O(log n) | |
O(n log n) | |
O(n log log n) |
Question 23 |
An array X of n distinct integers is interpreted as a complete binary tree. The index of the first element of the array is 0. If the root node is at level 0, the level of element X[i], i ≠ 0, is
⌊log2 i⌋ | |
⌈log2 (i + 1)⌉ | |
⌊log2 (i + 1)⌋ | |
⌈log2 i⌉ |
Question 24 |
When searching for the key value 60 in a binary search tree, nodes containing the key values 10, 20, 40, 50, 70 80, 90 are traversed, not necessarily in the order given. How many different orders are possible in which these key values can occur on the search path from the root to the node containing the value 60?
35 | |
64 | |
128 | |
5040 |
Smaller values 90, 80 and 70 are visited in order
i.e., 7!/(4!3!) = 35
Question 25 |
The following three are known to be the preorder, inorder and postorder sequences of a binary tree. But it is not known which is which.
MBCAFHPYK KAMCBYPFH MABCKYFPHPick the true statement from the following.
I and II are preorder and inorder sequences, respectively | |
I and III are preorder and postorder sequences, respectively | |
II is the inorder sequence, but nothing more can be said about the other two sequences | |
II and III are the preorder and inorder sequences, respectively
|
So, out of the given sequence only I & II are having such kind of order, i.e., K at the beginning and at the last.
Therefore, II is the preorder and I is postorder and the sequence III will definitely be inorder.
Question 26 |
A Binary Search Tree (BST) stores values in the range 37 to 573. Consider the following sequence of keys.
I. 81, 537, 102, 439, 285, 376, 305 II. 52, 97, 121, 195, 242, 381, 472 III. 142, 248, 520, 386, 345, 270, 307 IV. 550, 149, 507, 395, 463, 402, 270
Suppose the BST has been unsuccessfully searched for key 273. Which all of the above sequences list nodes in the order in which we could have encountered them in the search?
II and III only | |
I and III only | |
III and IV only | |
III only |

Question 27 |
A Binary Search Tree (BST) stores values in the range 37 to 573. Consider the following sequence of keys.
I. 81, 537, 102, 439, 285, 376, 305 II. 52, 97, 121, 195, 242, 381, 472 III. 142, 248, 520, 386, 345, 270, 307 IV. 550, 149, 507, 395, 463, 402, 270
Which of the following statements is TRUE?
I, II and IV are inorder sequences of three different BSTs | |
I is a preorder sequence of some BST with 439 as the root | |
II is an inorder sequence of some BST where 121 is the root and 52 is a leaf | |
IV is a postorder sequence of some BST with 149 as the root |
B) False because if 439 is root then it should be first element in preorder.
C) This is correct.
D) False because if 149 is root, then it should be last element in postorder.
Question 28 |
A Binary Search Tree (BST) stores values in the range 37 to 573. Consider the following sequence of keys.
I. 81, 537, 102, 439, 285, 376, 305 II. 52, 97, 121, 195, 242, 381, 472 III. 142, 248, 520, 386, 345, 270, 307 IV. 550, 149, 507, 395, 463, 402, 270
How many distinct BSTs can be constructed with 3 distinct keys?
4 | |
5 | |
6 | |
9 |
2nCn/n+1 = 6C3/7 = 5
Question 29 |
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors. n3 can be expressed as
n1 + n2 - 1 | |
n1 - 2 | |
[((n1 + n2)/2)] | |
n2 - 1 |

n1 = 3
n2 = 1
n3 = 1
So, option (B) satisfies.
Question 30 |
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors. Starting with the above tree, while there remains a node v of degree two in the tree, add an edge between the two neighbors of v and then remove v from the tree. How many edges will remain at the end of the process?
2 * n1 – 3 | |
n2 + 2 * n1 – 2 | |
n3 – n2 | |
n2 + n1 – 2 |
n1 = 3
n3 = 1
So, option (A) satisfies.
Question 31 |
It is possible to construct a binary tree uniquely whose pre-order and post-order traversals are given?
True | |
False |
Question 32 |
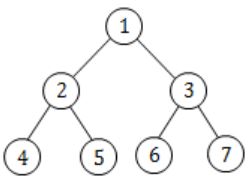
If the number of leaves in a tree is not a power of 2, then the tree is not a binary tree.
True | |
False |
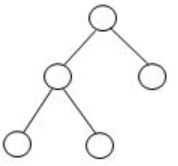
In the above binary tree, no. of leaves is 3, which is not the power of 2. Hence the given statement is false.
Question 33 |
The weighted external path length of the binary tree in figure is _____

144 |
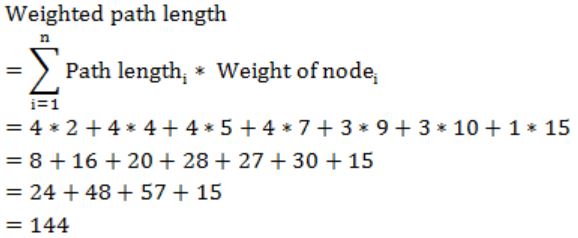
Question 34 |
Consider the binary tree in Figure:

(a) What structure is represented by the binary tree?
(b) Give the different steps for deleting the node with key 5 so that the structure is preserved.
(c) Outline a procedure in pseudo-code to delete an arbitrary node from such a binary tree with n nodes that preserves the structure. What is the worst-case time-complexity of your procedure?
Theory Explanation. |
Question 35 |
Choose the correct alternatives (More than one may be correct). The number of rooted binary trees with n nodes is,
Equal to the number of ways of multiplying (n+1) matrices. | |
Equal to the number of ways of arranging n out of 2n distinct elements. | |
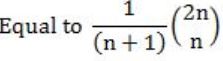 | |
Equal to n! | |
Both (A) and (C). |
Here, both options A and C are true as option A corresponds to n multiply operations of (n+1) matrices, the no. of ways for this is again given by the nth catalan number.
