CRC
Question 1 |
Consider the cyclic redundancy check (CRC) based error detecting scheme having the generator polynomial X3+X+1. Suppose the message m4m3m2m1m0=11000 is to be transmitted. Check bits c2c1c0are appended at the end of the message by the transmitter using the above CRC scheme. The transmitted bit string is denoted by m4m3m2m1m0c2c1c0. The value of the checkbit sequence c2c1c0is
111 | |
100 | |
101 | |
110 |
Question 1 Explanation:

Question 2 |
A computer network uses polynomials over GF(2) for error checking with 8 bits as information bits and uses x3 + x + 1 as the generator polynomial to generate the check bits. In this network, the message 01011011 is transmitted as
01011011010 | |
01011011011 | |
01011011101 | |
01011011100 |
Question 2 Explanation:
Given CRC generator polynomial = x3+x+1
= 1∙x3+0∙x2+1∙x1+1∙x0
= 1011
Message = 01011011
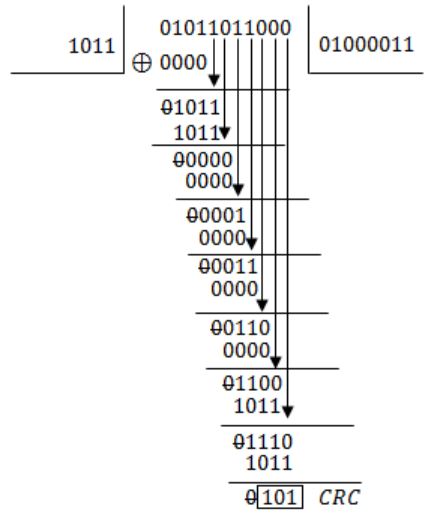
So, the message 01011011 is transmitted as
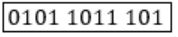
= 1∙x3+0∙x2+1∙x1+1∙x0
= 1011
Message = 01011011

So, the message 01011011 is transmitted as
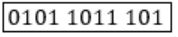
Question 3 |
The message 11001001 is to be transmitted using the CRC polynomial x3+1 to protect it from errors. The message that should be transmitted is:
11001001000 | |
11001001011 | |
11001010 | |
110010010011 |
Question 3 Explanation:
CRC polynomial = x3+1 [∵ In data 3-zero’s need to be append to data]
= 1001

∴ Data transmitted is: 11001001011
= 1001

∴ Data transmitted is: 11001001011
There are 3 questions to complete.
