Cache
Question 1 |
0.85 |
h1 = 0.8
t1 = 10 ns
t2 = 100ns
After the optimization the average memory access time remains the same,
Let the new hit rate be h2. The new cache access time is 15ns.
Applying the average access time formula h1t1+(1-h1)(t1+t2)
0.8*10+0.2*(10+100) = h2*15+(1-h2)(15+100)
30 = 15 + (1-h2)*100
1-h2 = 0.15
h2 = 0.85
Question 2 |
The TLB performs an associative search in parallel on all its valid entries using page number of incoming virtual address. | |
If the virtual address of a word given by CPU has a TLB hit, but the subsequent search for the word results in a cache miss, then the word will always be present in the main memory. | |
The memory access time using a given inverted page table is always same for all incoming virtual addresses. | |
In a system that uses hashed page tables, if two distinct virtual addresses V1 and V2 map to the same value while hashing, then the memory access time of these addresses will not be the same. |
(B) True: TLB hit implies no page fault. Hence, the page-frame will always be in main memory.
(C) False: Inverted page table depends on the size of the process. Hence, the memory access time also varies.
(D) True: Collision resolution techniques are applied. Hence, the each address may take different time.
Question 3 |
Every access to S is a hit. | |
Once P is brought to the cache it is never evicted. | |
At the end of the execution only R and S reside in the cache. | |
Every access to R evicts Q from the cache. |
Block size = 64 bytes = 2^6 bytes, we need 6 bits OFFSET to identify each byte in the block.
No. of blocks in the cache = 2^11 / 2^6 = 2^5, since it is a direct mapped cache we need 5 bits in the physical address to identify the LINE number.
Each word is 16 bits long = 2 bytes.
Number of words in each block = 64/2 = 32 words.
The physical memory is 64KB = 2^16 bytes, so the physical address is 16 bits.
In direct mapped cache the physical address is divided into (TAG, LINE, OFFSET)
In the 16 bits physical address OFFSET is 6 bits and LINE number is 5 bits, so there are 5 TAG bits.
The given physical addresses of P, Q, R, S can be written in binary as below (each hexadecimal digit represents 4 binary digits):
P: 0xA248 (10100 01001 001000 )
Q: 0xC28A (11000 01010 001010)
R: 0xCA8A (11001 01010 001010)
S: 0xA262 (10100 01001 100010)
Here P is mapped to line number 9 in the cache. S also is mapped to line number 9 and not only that they both are from the same block as even the TAG bits are matching. So, even the first access of S will be a hit as it gets prefetched along with P. Once P is fetched it is never evicted.
Both Q and R are mapped to line number 10 in the cache. But they are from different blocks as the TAG bits are different. Since it is a direct mapped cache, every access of R evicts Q from the cache.
Hence options A, B, D are true. Option C is false as at the end of execution P, R, S are in the cache not just R, S.
Question 4 |
A direct mapped cache memory of 1 MB has a block ize of 256 bytes. The cache has an access time of 3 ns and a hit rate of 94%. During a cache miss, it takes 20 ns to bring the first word of a block from the main memory, while each subsequent word takes 5 ns. The word size is 64 bits. The average memory access time in ns (round off to 1 decimal place) is _____.
13.5 |
Hit ratio of cache = 0.94
Word size is 64 bits = 8 bytes.
Cache line size = 256 bytes = 32 words
Main memory access time = 20ns(time for first word) + 155ns(time for remaining 31 words, 31*5 = 155ns) = 175 ns
Average access time = h1*t1 + (1-h1)(t1+t2) = t1 +(1-h1)t2
⇒ 3 + (0.06)(175) = 13.5 ns
Question 5 |
A computer system with a word length of 32 bits has a 16 MB byte-addressable main memory and a 64 KB, 4-way set associative cache memory with a block size of 256 bytes. Consider the following four physical addresses represented in hexadecimal notation.
A1 = 0x42C8A4, A2 = 0x546888, A3 = 0x6A289C, A4 = 0x5E4880
Which one of the following is TRUE?
A1 and A4 are mapped to different cache sets. | |
A1 and A3 are mapped to the same cache set. | |
A3 and A4 are mapped to the same cache set. | |
A2 and A3 are mapped to the same cache set. |
The word length is given as 32 bits and the physical addresses mentioned are all contain 6 hexadecimal digits, so the the physical address is 32 bits long.
Block size is 256 bytes, block offset = 8 bits as it is a byte addressable memory.
Cache size = 64KB
Number of blocks in the cache = 64KB/256B = 256
It is a 4-way set associative cache, so no. of sets in the cache = 256/4 = 64 = 26
In the physical address we need 6 bits for the SET number.
TAG bits = 32 - 6 - 8 = 18
So the 32 bits physical address is divided as (18 TAG bits + 6 SET number bits + 8 OFFSET bits)
Since in all the options we are asked about SET numbers of the given addresses, we need to find the SET number of each of the addresses.
A1 = 0x42C8A4, here SET number is (00 1000) which includes the last 2 bits of C(1100) and binary representation of 8 (1000).
A2 = 0x546888, here SET number is (10 1000) which includes the last 2 bits of 6(0110) and binary representation of 8 (1000).
A3 = 0x6A289C here SET number is (10 1000) which includes the last 2 bits of 2(0010) and binary representation of 8 (1000).
A4 = 0x5E4880 here SET number is (00 1000) which includes the last 2 bits of 4 (0100) and binary representation of 8 (1000).
From the given options option-4 is TRUE as A2, A3 are mapped to the same cache SET.
Question 6 |
Consider a two-level cache hierarchy with L1 and L2 caches. An application incurs 1.4 memory accesses per instruction on average. For this application, the miss rate of L1 cache is 0.1; the L2 cache experiences, on average, 7 misses per 1000 instructions. The miss rate of L2 expressed correct to two decimal places is __________.
0.05 | |
0.06 | |
0.07 | |
0.08 |
For 1000 instructions total number of memory references = 1000 * 1.4 = 1400
These 1400 memory references are first accessed in the L1.
Since the miss rate of L1 is 0.1, for 1400 L1 references the number of misses = 0.1 * 1400 = 140
We know when there is a miss in L1 we next access the L2 cache.
So number of memory references to L2 = 140
It is given that there are 7 misses in L2 cache. Out of 140 memory references to L2 cache there are 7 misses.
Hence the miss rate in L2 cache = 7/140 = 0.05
Question 7 |
Consider a 2-way set associative cache with 256 blocks and uses LRU replacement. Initially the cache is empty. Conflict misses are those misses which occur due to contention of multiple blocks for the same cache set. Compulsory misses occur due to first time access to the block. The following sequence of accesses to memory blocks
(0, 128, 256, 128, 0, 128, 256, 128, 1, 129, 257, 129, 1, 129, 257, 129)is repeated 10 times. The number of conflict misses experienced by the cache is __________.
76 | |
79 | |
80 | |
81 |
If a block is accessed once and then before its second access if there are k-unique block accesses and the cache size is less than k, and in that case if the second access is amiss then it is capacity miss. In this case the cache doesn't have the size to hold all the k-unique blocks that came and so when the initial block came back again it is not in the cache because capacity of the cache is less than the unique block accesses k. Hence it is capacity miss.
If a block is accessed once and then before its second access if there are k-unique block accesses and the cache size is greater than k, and in that case if the second access is a miss then it is conflict miss. In this case the cache can hold all the k-unique blocks that came and even then when the initial block came back again it is not in the cache because it got replaced, then it is conflict miss.
LRU will use the function xmod128
Cache size = 256 Bytes
2 way set associative cache
So, no. of cache sets = 256/2 = 128
Blue → Compulsory miss
Red → Conflict miss
At the end of first round we have 4, compulsory misses & 4 conflict misses.
Similarly, if we continue from Round-2 to last round, in every round we will get 8 conflict misses.
Total conflict misses = 4+9(8) = 4+72 = 76 (conflict misses)
Question 8 |
A cache memory unit with capacity of N words and block size of B words is to be designed. If it is designed as a direct mapped cache, the length of the TAG field is 10 bits. If the cache unit is now designed as a 16-way set-associative cache, the length of the TAG field is ___________ bits.
14 | |
15 | |
16 | |
17 |
(Tag bits + bits for block number + bits for block offset)
With block size being B words no. of bits for block offset = log (B)
Because the cache capacity is N words and each block is B words, number of blocks in cache = N / B
No. of bits for block number = log (N/B)
So, the physical address in direct mapping case
= 10 + log (N/B) + log (B)
= 10 + log (N) – log B + log B
= 10 + log (N)
If the same cache unit is designed as 16-way set associative, then the physical address becomes
(Tag bits + bits for set no. + Bits for block offset)
There are N/B blocks in the cache and in 16-way set associative cache each set contains 16 blocks.
So no. of sets = (N/B) / 16 = N / (16*B)
Then bits for set no = log (N/16B)
Bits for block offset remain the same in this case also. That is log (B).
So physical address in the set associative case
= tag bits + log (N/16*B) + log B
= tag bits + log (N) – log (16*B) + log B
= tag bits + log (N) – log 16 – log B + log B
= tag bits + log N – 4
The physical address is the same in both the cases.
So, 10 + log N = tag bits + log N – 4
Tag bits = 14
So, no. of tag bits in the case 16-way set associative mapping for the same cache = 14.
Question 9 |
The main memory of a computer has 2 cm blocks while the cache has 2c blocks. If the cache uses the set associative mapping scheme with 2 blocks per set, then block k of the main memory maps to the set
(k mod m) of the cache | |
(k mod c) of the cache | |
(k mod 2c) of the cache | |
(k mod 2 cm) of the cache |
= 2c/c
= c
∴ Cache set no. to which block k of main memory maps to
= (Main memory block no.) mod (Total set in cache)
= k mod c
Question 10 |
More than one word is put in one cache block to
exploit the temporal locality of reference in a program | |
exploit the spatial locality of reference in a program | |
reduce the miss penalty | |
none of the above |
The temporal locality refers to reuse of data elements with a smaller regular intervals.
Question 11 |
A CPU has 32-bit memory address and a 256 KB cache memory. The cache is organized as a 4-way set associative cache with cache block size of 16 bytes.
- (a) What is the number of sets in the cache?
(b) What is the size (in bits) of the tag field per cache block?
(c) What is the number and size of comparators required for tag matching?
(d) How many address bits are required to find the byte offset within a cache block?
(e) What is the total amount of extra memory (in bytes) required for the tag bits?
Theory Explanation is given below. |
Question 12 |
In a C program, an array is declared as float A[2048]. Each array element is 4 Bytes in size, and the starting address of the array is 0×00000000. This program is run on a computer that has a direct mapped data cache of size 8 Kbytes, with block (line) size of 16 Bytes.
(a) Which elements of the array conflict with element A[0] in the data cache? Justify your answer briefly.
(b) If the program accesses the elements of this array one by one in reverse order i.e., starting with the last element and ending with the first element, how many data cache misses would occur? Justify your answer briefly. Assume that the data cache is initially empty and that no other data or instruction accesses are to be considered.
Theory Explanation is given below. |
Question 13 |
Consider a small two-way set-associative cache memory, consisting of four blocks. For choosing the block to be replaced, use the least recently used (LRU) scheme. The number of cache misses for the following sequence of block addresses is 8, 12, 0, 12, 8
2 | |
3 | |
4 | |
5 |
The given sequence is 8, 12, 0, 12, 8.
So in total 4 misses is there.
Question 14 |
In the three-level memory hierarchy shown in the following table, pi denotes the probability that an access request will refer to Mi.
If a miss occurs at level Mi, a page transfer occurs from Mi+1 to Mi and the average time required for such a page swap is Ti. Calculate the average time tA required for a processor to read one word from this memory system.
Theory Explanation. |
Question 15 |
2 |
Cache size = 2KB
Block size = 64 Bytes = 2^6 bytes. So the OFFSET is 6 bits long.
The TAG field is 22 bits. And the physical address is 32 bits.
Since it is given as a set associative cache, the physical address is divided as (TAG, SET, OFFSET).
From the given information we can find the SET number = 32 - 22 - 6 = 4 bits.
Using the 4 SET bits, the number of sets possible = 2^4 = 16.
Number of blocks in the cache = Cache size / Block size = 2KB / 64 = 2^11/2^6 = 2^5.
Number of sets in the cache = Number of blocks in the cache / Number of blocks in each set
Number of blocks in each set is also called the associativity.
16 = 2^5/associativity
Associativity = 2^5/16 = 2
Question 16 |
S1:Read misses in a write through L1 cache do not result in writebacks of dirty lines to the L2.
S2:Write allocate policy must be used in conjunction with write through caches and no-write allocate policy is used with write back caches.
S1is true and S2is false | |
S1is false and S2is false | |
S1is true and S2is true | |
S1is false and S2is true |
S1: In a write through cache the writing happens to both the L1 and L2 caches simultaneously. It is also given as the inclusive hierarchy. Here L1 is a subset of L2. So when there is a cache read miss in L1 we try to fetch the content from L2. If the block containing that missed word is dirty in the L1 cache, since it is a write through cache the same content would have also been written to the L2 cache also earlier itself. So there is no need to write back the dirty lines again to the L2 cache on a cache miss. Hence S1 is true.
S2: Generally no-write allocate is used with write through cache and write allocate is used with write back cache. Hence S2 is false.
Question 17 |
Consider a system with 2 level caches. Access times of Level 1 cache, Level 2 cache and main memory are 1 ns, 10ns, and 500 ns, respectively. The hit rates of Level 1 and Level 2 caches are 0.8 and 0.9, respectively. What is the average access time of the system ignoring the search time within the cache?
13.0 ns | |
12.8 ns | |
12.6 ns | |
12.4 ns |
H1 = 0.8, (1 - H1) = 0.2
H2 = 0.9, (1 - H2) = 0.1
T1 = Access time for level 1 cache = 1ns
T2 = Access time for level 2 cache = 10ns
Hm = Hit rate of main memory = 1
Tm = Access time for main memory = 500ns
Average access time = [(0.8 * 1) + (0.2 * 0.9 * 10) + (0.2)(0.1) * 1 * 500]
= 0.8 + 1.8 + 10
= 12.6ns
Question 18 |
A dynamic RAM has a memory cycle time of 64 nsec. It has to be refreshed 100 times per msec and each refresh takes 100 nsec. What percentage of the memory cycle time is used for refreshing?
10 | |
6.4 | |
1 | |
.64 |
In 106ns refresh 100 times.
Each refresh takes 100ns.
Memory cycle time = 64ns
Refresh time per 1ms i.e., per 106ns = 100 * 100 = 104ns
Refresh time per 1ns = (104)/(106) ns
Refresh time per cycle = (104*64)/(106) = 64ns
Percentage of the memory cycle time is used for refreshing = (64*100)/64 = 1%
Question 19 |
A cache line is 64 bytes. The main memory has latency 32 ns and bandwidth 1 GBytes/s. The time required to fetch the entire cache line from the main memory is
32 ns | |
64 ns | |
96 ns | |
128 ns |
→ So, for 64 bytes it will take 64*1/109 = 64ns.
Main memory latency = 32
Total time required to place cache line is
64+32 = 96 ns
Question 20 |
A computer system has a level-1 instruction cache (1-cache), a level-1 data cache (D-cache) and a level-2 cache (L2-cache) with the following specifications:
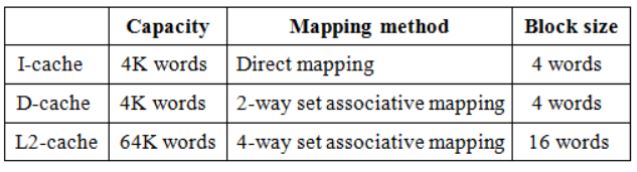
The length of the physical address of a word in the main memory is 30 bits. The capacity of the tag memory in the I-cache, D-cache and L2-cache is, respectively,
1K × 18-bit, 1K × 19-bit, 4K × 16-bit | |
1K × 16-bit, 1K × 19-bit, 4K × 18-bit | |
1K × 16-bit, 512 × 18-bit, 1K × 16-bit | |
1K × 18-bit, 512 × 18-bit, 1K × 18-bit |
Bits to represent blocks = m
No. of words in a block = 2n
Bits to represent a word = n
Tag bits = (length of physical address of a word) - (bits to represent blocks) - (bits to represent a word)
⇒ Each block will have its own tag bits.
So, total tag bits = no. of blocks × tag bits.
Question 21 |
Consider a Direct Mapped Cache with 8 cache blocks (numbered 0-7). If the memory block requests are in the following order
3, 5, 2, 8, 0, 63, 9,16, 20, 17, 25, 18, 30, 24, 2, 63, 5, 82,17, 24.Which of the following memory blocks will not be in the cache at the end of the sequence?
3 | |
18 | |
20 | |
30 |
So memory block 18 is not in the cache.
Question 22 |
Consider a computer with a 4-ways set-associative mapped cache of the following characteristics: a total of 1 MB of main memory, a word size of 1 byte, a block size of 128 words and a cache size of 8 KB. The number of bits in the TAG, SET and WORD fields, respectively are:
7, 6, 7 | |
8, 5, 7 | |
8, 6, 6 | |
9, 4, 7 |
No. of sets in cache = 26/22 = 24
So no. of set bits = 4
Size of block = 128 words = 128 B = 27
So no. of word bit = 7
So tag bits = 20 - 4 - 7 = 9
Question 23 |
Consider a computer with a 4-ways set-associative mapped cache of the following characteristics: a total of 1 MB of main memory, a word size of 1 byte, a block size of 128 words and a cache size of 8 KB. While accessing the memory location 0C795H by the CPU, the contents of the TAG field of the corresponding cache line is
000011000 | |
110001111 | |
00011000 | |
110010101 |
So lets first convert given Hexadecimal no. into binary number,
Question 24 |
State whether the following statements are TRUE or FALSE with reason:
Transferring data in blocks from the main memory to the cache memory enables an interleaved main memory unit to operate at its maximum speed.True | |
False |
Question 25 |
The width of the physical address on a machine is 40 bits. The width of the tag field in a 512 KB 8-way set associative cache is _________ bits.
24 | |
25 | |
26 | |
27 |
(Tag bits + bits for set no. + Bits for block offset)
In question block size has not been given, so we can assume block size 2x Bytes.
The cache is of size 512KB, so number of blocks in the cache = 219/2x = 219-x
It is 8-way set associative cache so there will be 8 blocks in each set.
So number of sets = (219 − x)/8 = 216 − x
So number of bits for sets = 16−x
Let number of bits for Tag = T
Since we assumed block size is 2x Bytes, number of bits for block offset is x.
So, T + (16−x) + x = 40
T + 16 = 40
T = 24
Question 26 |
A file system uses an in-memory cache to cache disk blocks. The miss rate of the cache is shown in the figure. The latency to read a block from the cache is 1 ms and to read a block from the disk is 10 ms. Assume that the cost of checking whether a block exists in the cache is negligible. Available cache sizes are in multiples of 10 MB.
The smallest cache size required to ensure an average read latency of less than 6 ms is _______ MB.
30 | |
31 | |
32 | |
33 |
So we consider it as hierarchical memory.
But it is given that “assume that the cost of checking whether a block exists in the cache is negligible”, which means don't consider the checking time in the cache when there is a miss.
So formula for average access time becomes h1t1 + (1-h1)(t2) which is same as for simultaneous access.
Though the memory is hierarchical because of the statement given in the question we ignored the cache access time when there is a miss and effectively the calculation became like simultaneous access.
The average access time or read latency = h1t1 + (1-h1)t2.
It is given that the average read latency has to be less than 6ms.
So, h1t1 + (1-h1)t2 < 6
From the given information t1 = 1ms, t2 = 10ms
h1*1+(1-h1)10 < 6
10-9h1 < 6
-9h1 < - 4
-h1 < - 4/9
-h1 < -0.444
Since in the given graph we have miss rate information and 1-h1 gives the miss rate, so we add 1 on both sides of the above inequality.
1-h1 < 1-0.444
1-h1 < 0.555
So for the average read latency to be less than 6 ms the miss rate hsa to be less than 55.5%.
From the given graph the closest value of miss rate less than 55.5 is 40%.
For 40% miss rate the corresponding cache size is 30MB.
Hence the answer is 30MB.