Deadlock
Question 1 |
function OWNRESOURCE(Resource R)
Acquire lock L // a global lock
if R is available then
Acquire R
Release lock L
else
if R is owned by another process P then
Terminate P, after releasing all resources owned by P
Acquire R
Restart P
Release lock L
end if
end if
end function
Which of the following choice(s) about the above scheme is/are correct?
The scheme ensures that deadlocks will not occur. | |
The scheme may lead to live-lock. | |
The scheme violates the mutual exclusive property. | |
The scheme may lead to starvation. |
(1) True,
The scheme ensures deadlock free operation, as there is no hold-and-wait condition possible.
(2) True,
The scheme may lead to priority inversion problems, and hence livelock is possible.
(3) False,
Mutual exclusion is satisfied as only one process can acquire and release locks at a time.
(4) True,
The scheme may lead to starvation. For example, the priority process can get scheduled repeatedly and keeps on killing the lower priority processes. Hence, a low priority process may strave.
Question 2 |
Which of the following is an example of spooled device?
A line printer used to print the output of a number of jobs. | |
A terminal used to enter input data to a running program. | |
A secondary storage device in a virtual memory system. | |
A graphic display device. |
Question 3 |
A solution to the Dining Philosophers Problem which avoids deadlock is
ensure that all philosophers pick up the left fork before the right fork | |
ensure that all philosophers pick up the right fork before the left fork | |
ensure that one particular philosopher picks up the left fork before the right fork, and that all other philosophers pick up the right fork before the left fork | |
None of the above |
To avoid this, atleast one philosopher should choose its first chopstick in different way so that circular loop is not formed.
Question 4 |
A computer system uses the Banker’s Algorithm to deal with deadlocks. Its current state is shown in the table below, where P0, P1, P2 are processes, and R0, R1, R2 are resources types.
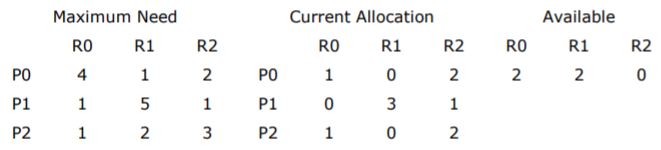
(a) Show that the system can be in this state.
(b) What will the system do on a request by process P0 for one unit of resource type R1?
Theory Explanation. |
Question 5 |
An operating system contains 3 user processes each requiring 2 units of resource R. The minimum number of units of r such that no deadlocks will ever arise is
3 | |
5 | |
4 | |
6 |
Question 6 |
Consider a system with 3 processes that share 4 instances of the same resource type. Each process can request a maximum of K instances. Resource instances can be requested and released only one at a time. The largest value of K that will always avoid deadlock is _________.
2 | |
3 | |
4 | |
5 |
No. of resources = 4
Let’s distribute each process one less than maximum demands i.e., (k-1) resources.
So, for three processes, 3(k – 1) resources.
For deadlock avoidance provide an additional resource to any one of the process.
∴ Total resources required to avoid deadlock in any case is 3(k – 1) + 1 = 3k – 2
Now this 3k – 2 should be less than equal to available no. of resources, i.e.,
3k – 2 ≤ 4
k ≤ 2
So maximum value of k = 2
Question 7 |
In a system, there are three types of resources: E, F and G. Four processes P0, P1, P2 and P3 execute concurrently. At the outset, the processes have declared their maximum resource requirements using a matrix named Max as given below. For example, Max[P2, F] is the maximum number of instances of F that P2 would require. The number of instances of the resources allocated to the various processes at any given state is given by a matrix named Allocation.
Consider a state of the system with the Allocation matrix as shown below, and in which 3 instances of E and 3 instances of F are the only resources available.

From the perspective of deadlock avoidance, which one of the following is true?
The system is in safe state. | |
The system is not in safe state, but would be safe if one more instance of E were available. | |
The system is not in safe state, but would be safe if one more instance of F were available.
| |
The system is not in safe state, but would be safe if one more instance of G were available. |
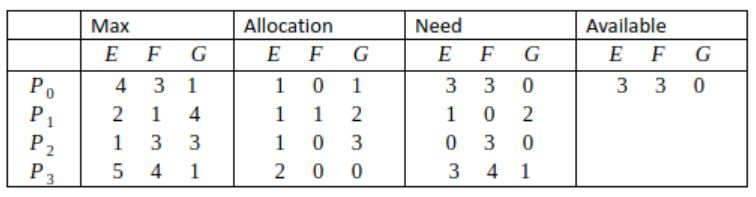
Safe sequence:
〈P0, P2, P1, P3〉
P0: P0 can be allotted 〈3,3,0〉.
After completion Available = 〈4,3,1〉
P2: P2 can be allotted 〈0,3,0〉.
After completion: Available = 〈5,3,4〉
P1: P1 can be allotted 〈1,0,2〉.
After completion: Available = 〈6,4,6〉
P3: P3 can be allotted 〈3,4,1〉.
After completion: Available = 〈8,4,6〉
Question 8 |
Which of the following is an example of a spooled device?
The terminal used to enter the input data for the C program being executed | |
An output device used to print the output of a number of jobs | |
The secondary memory device in a virtual storage system | |
The swapping area on a disk used by the swapper |
For example in printer if a process attempt to print a document but printer is busy printing another document, the process, instead of waiting for printer to become available, write its output to disk. When the printer becomes available the data on disk is printed.
Spooling allows process to request operation from peripheral device without requiring that the device is ready to service the request.
Question 9 |
A computer has six tape drives, with n processes competing for them. Each process may need two drives. What is the maximum value of n for the system to be deadlock free?
6 | |
5 | |
4 | |
3 |
So maximum no. of process for the system to be deadlock free is 5.
Question 10 |
Which of the following is NOT a valid deadlock prevention scheme?
Release all resources before requesting a new resource | |
Number the resources uniquely and never request a lower numbered resource than the last one requested | |
Never request a resource after releasing any resource | |
Request and all required resources be allocated before execution |
Question 11 |
Consider a system having m resources of the same type. These resources are shared by 3 processes A, B and C, which have peak demands of 3, 4 and 6 respectively. For what value of m deadlock will not occur?
7 | |
9 | |
13, 15 | |
13 | |
15 |
→ If A have 2, B have 3, C have 5 then deadlock will occur i.e., 2+3+5=10.
→ If we have one extra resource then deadlock will not occur i.e., 10+1=11.
→ If we have equal (or) more than 11 resources then deadlock will never occur.
Question 12 |
Assume that the following jobs are to be executed on a single processor system

The jobs are assumed to have arrived at time 0+ and in the order p, q, r, s, t. Calculate the departure time (completion time) for job p if scheduling is round robin with time slice 1.
4 | |
10 | |
11 | |
12 | |
None of the above |

p is departure at 11.
Question 13 |
A computer system has 6 tape drives, with n process completing for them. Each process may need 3 tape drives. The maximum value of n for which the system is guaranteed to be deadlock free is:
2 | |
3 | |
4 | |
1 |
Question 14 |
Circular wait is a necessary condition for the formation of deadlock. | |
In a system where each resource has more than one instance, a cycle in its wait-for graph indicates the presence of a deadlock. | |
If the current allocation of resources to processes leads the system to unsafe state, then deadlock will necessarily occur. | |
In the resource-allocation graph of a system, if every edge is an assignment edge, then the system is not in deadlock state. |
Question 15 |
Two shared resources R1 and R2 are used by processes P1 and P2. Each process has a certain priority for accessing each resource. Let Tij denote the priority of Pi for accessing Rj. A process Pi can snatch a resource Rh from process Pj if Tik is greater than Tjk. Given the following:
(I) T11 > T21 (II) T12 > T22 (III) T11 < T21 (IV) T12 < T22Which of the following conditions ensures that P1 and P2 can never deadlock?
(I) and (IV) | |
(II) and (III) | |
(I) and (II) | |
None of the above |
Question 16 |
An operating system implements a policy that requires a process to release all resources before making a request for another resource. Select the TRUE statement from the following:
Both starvation and deadlock can occur | |
Starvation can occur but deadlock cannot occur | |
Starvation cannot occur but deadlock can occur | |
Neither starvation nor deadlock can occur |
Now, maybe the process has not used the resources it released yet. This may happen again when the process requests another resource.
So, the process starved for proper utilization of resources.
Deadlock will not occur as it is one of the deadlock prevention scheme.
Question 17 |
Suppose n processes, P1, …., Pn share m identical resource units, which can be reserved and released one at a time. The maximum resource requirement of process Pi is si, where si>0. Which one of the following is a sufficient condition for ensuring that deadlock does not occur?
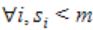 | |
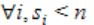
| |
 | |
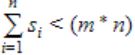 |
If the deadlock will never occur in the corresponding process then the following condition be true.

Question 18 |
A system shares 9 tape drives. The current allocation and maximum requirement of tape drives for three processes are shown below:
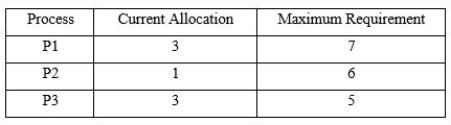
Which of the following best describe current state of the system?
Safe, Deadlocked | |
Safe, Not Deadlocked | |
Not Safe, Deadlocked | |
Not Safe, Not Deadlocked |
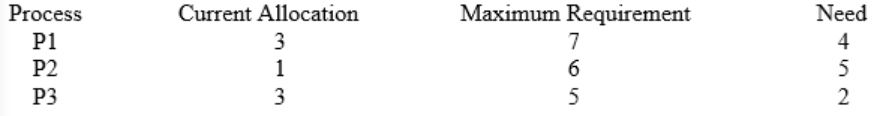
Available: (9 - (3 + 1 + 3)) = 2, P3 can be satisfied.
New available = 3 + 2 = 5
Now, P2 can be satisfied.
New available: 5 + 1 = 6
Now, P1 can be satisfied. Thus safe sequence: P3 → P2 → P1
That is not deadlocked.
Question 19 |
A system has 6 identical resources and N processes competing for them. Each process can request atmost 2 resources. Which one of the following values of N could lead to a deadlock?
1 | |
2 | |
3 | |
6 |
Question 20 |
Consider the following snapshot of a system running n concurrent processes. Process i is holding Xi instances of a resource R, 1 ≤ i ≤ n. Assume that all instances of R are currently in use. Further, for all i, process i can place a request for at most Yi additional instances of R while holding the Xi instances it already has. Of the n processes, there are exactly two processes p and q such that Yp = Yq = 0. Which one of the following conditions guarantees that no other process apart from p and q can complete execution?
Min (Xp, Xq) ≥ Min {Yk | 1 ≤ k ≤ n, k ≠ p, k ≠ q} | |
Xp + Xq < Max {Yk | 1 ≤ k ≤ n, k ≠ p, k ≠ q} | |
Min (Xp, Xq) ≤ Max {Yk | 1 ≤ k ≤ n, k ≠ p, k ≠ q} | |
Xp + Xq < Min {Yk | 1 ≤ k ≤ n, k ≠ p, k ≠ q} |
Pi holds Xi instances.
Pi can request additional Yi instances.
Given two process p & q such that their additional requests are zero.
Yp = Yq = 0
{Yk | 1 ≤ k ≤ n, k ≠ p, k ≠ q} means that out of 'n' processes, we are left with (n-2) process (except p&q), i.e., Yk indicates additional request of all the processes (n-2) except p & q.
For p & q to complete first, accordingly
Xp + Xq < Min {Yk}
Option D is correct.
There are exactly two process p and q which do not need any additional instances of resources.
So, p and q will complete their execution and will release Xp and Xq instances of resources.
Now to guarantee that no other process apart from p and q can complete execution, the no. of instances of resources available must be less than the minimum no. of instances of resources required by any other process, i.e.,
Xp + Xq < Min {Yk | 1 ≤ k ≤ n, k ≠ p, k ≠ q}.
Question 21 |
Consider the following policies for preventing deadlock in a system with mutually exclusive resources.
- I. Processes should acquire all their resources at the beginning of execution. If any resource is not available, all resources acquired so far are released.
II. The resources are numbered uniquely, and processes are allowed to request for resources only in increasing resource numbers.
III. The resources are numbered uniquely, and processes are allowed to request for resources only in decreasing resource numbers.
IV. The resources are numbered uniquely. A process is allowed to request only for a resource with resource number larger than its currently held resources.
Which of the above policies can be used for preventing deadlock?
Any one of I and III but not II or IV | |
Any one of I, III, and IV but not II | |
Any one of II and III but not I or IV | |
Any one of I, II, III, and IV |
Question 22 |
A system has n resources R0,...,Rn-1,and k processes P0,....Pk-1.The implementation of the resource request logic of each process Pi is as follows:
if (i % 2 == 0) {
if (i < n) request Ri
if (i+2 < n) request Ri+2
}
else {
if (i < n) request Rn-i
if (i+2 < n) request Rn-i-2
}
In which one of the following situations is a deadlock possible?
n = 40, k = 26 | |
n = 21, k = 12 | |
n = 20, k = 10 | |
n = 41, k = 19 |
P10 requests R10 & R11
P11 requests R10 & R8
Hence P10 & P11 inorder in deadlock.
