Greedy-Algorithm
Question 1 |
Suppose P, Q, R, S, T are sorted sequences having lengths 20, 24, 30, 35, 50 respectively. They are to be merged into a single sequence by merging together two sequences at a time. The number of comparisons that will be needed in the worst case by the optimal algorithm for doing this is ______.
358 | |
359 | |
360 | |
361 |
Question 1 Explanation:
The implementation of optimal algorithm for merging sequences is as follows.
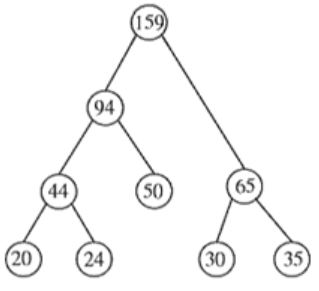
In the above implementation, total number of comparisons is
(44-1) + (94-1) + (65-1) + (159-1) = 358
Hint: The number of comparisons for merging two sorted sequences of length m and n is m+n-1.

In the above implementation, total number of comparisons is
(44-1) + (94-1) + (65-1) + (159-1) = 358
Hint: The number of comparisons for merging two sorted sequences of length m and n is m+n-1.
There is 1 question to complete.
