Heap-Tree
Question 1 |
Consider the array representation of a binary min-heap containing 1023 elements. The minimum number of comparisons required to find the maximum in the heap is _______.
511 |
n=1023
= Ceil(1023/2)
= 512
So, the maximum element is also part of n/2.
So, we have to subtract from the total elements
= 512-1
= 511
Question 2 |
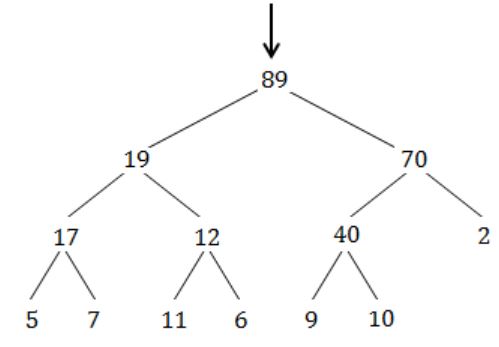
The minimum number of interchanges needed to convert the array
89, 19, 40, 17, 12, 10, 2, 5, 7, 11, 6, 9, 70
into a heap with the maximum element at the root is
0 | |
1 | |
2 | |
3 |

Question 3 |
The number of possible min-heaps containing each value from {1, 2, 3, 4, 5, 6, 7} exactly once is ___________.
80 | |
81 | |
82 | |
83 |
--> After sorting, pick the minimum element and make it the root of the min heap.
--> So, there is only 1 way to make the root of the min heap.
--> Now we are left with 6 elements
Question 4 |
Consider any array representation of an n element binary heap where the elements are stored from index 1 to index n of the array. For the element stored at index i of the array (i≤n), the index of the parent is
i-1 | |
⌊i/2⌋ | |
⌈i/2⌉ | |
(i+1)/2 |
Left Child is at index: 2i
Right child is at index: 2*i+1
Question 5 |
In a heap with n elements with the smallest element at the root, the 7th smallest element can be found in time
Θ(n log n) | |
Θ(n) | |
Θ(log n) | |
Θ(1) |
1 + 2 + 4 + 6 + 8 + 16 + 32
Which is constant then we can find the 7th smallest element in Θ(1) time.
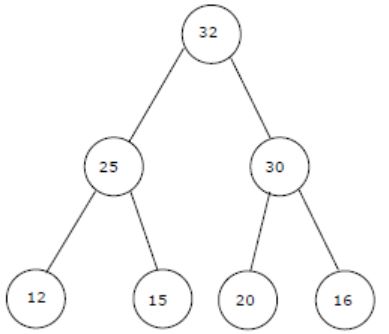
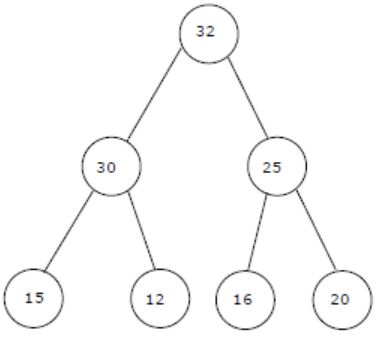
Question 6 |
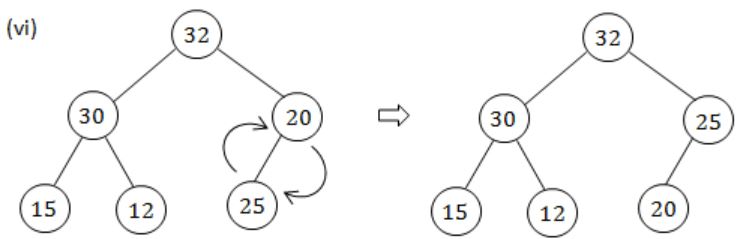
The elements 32, 15, 20, 30, 12, 25, 16 are inserted one by one in the given order into a Max Heap. The resultant Max Heap is
 | |
 | |
 | |
 |




Question 7 |
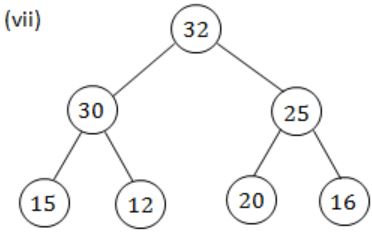
Which of the following sequences of array elements forms a heap?
{23, 17, 14, 6, 13, 10, 1, 12, 7, 5} | |
{23, 17, 14, 6, 13, 10, 1, 5, 7, 12} | |
{23, 17, 14, 7, 13, 10, 1, 5, 6, 12} | |
{23, 17, 14, 7, 13, 10, 1, 12, 5, 7} |
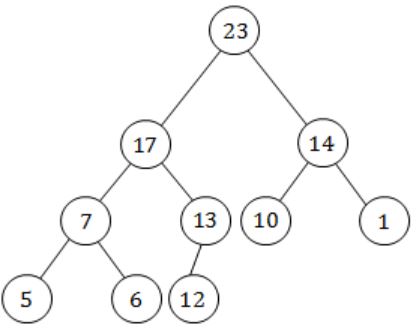
In this every children and parent satisfies Max heap properties.
Question 8 |
23, 17, 10, 6, 13, 14, 1, 5, 7, 12 | |
23, 17, 14, 7, 13, 10, 1, 5, 6, 12 | |
23, 17, 14, 6, 13, 10, 1, 5, 7, 15 | |
23, 14, 17, 1, 10, 13, 16, 12, 7, 5 |
Question 9 |
Consider a complete binary tree where the left and the right subtrees of the root are max-heaps. The lower bound for the number of operations to convert the tree to a heap is
Ω(logn) | |
Ω(n) | |
Ω(nlog n) | |
Ω(n2) |
