Memory-Management
Question 1 |
In a paged segmented scheme of memory management, the segment table itself must have a page table because
the segment table is often too large to fit in one page | |
each segment is spread over a number of pages | |
segment tables point to page table and not to the physical locations of the segment | |
the processor’s description base register points to a page table | |
Both A and B |
Segment paging is different from paged segmentation.
Question 2 |
The capacity of a memory unit is defined by the number of words multiplied by the number of bits/word. How many separate address and data lines are needed for a memory of 4K × 16?
10 address, 16 data lines | |
11 address, 8 data lines | |
12 address, 16 data lines | |
12 address, 12 data lines |
m = no. of address lines
n = no. of data lines
Given, 4K × 16 = 212 × 16
Address lines = 12
Data lines = 16
Question 3 |
A computer installation has 1000k of main memory. The jobs arrive and finish in the following sequences.
Job 1 requiring 200k arrives Job 2 requiring 350k arrives Job 3 requiring 300k arrives Job 1 finishes Job 4 requiring 120k arrives Job 5 requiring 150k arrives Job 6 requiring 80k arrives
(a) Draw the memory allocation table using Best Fit and First fit algorithms.
(b) Which algorithm performs better for this sequence?
Theory Explanation. |
Question 4 |
Consider allocation of memory to a new process. Assume that none of the existing holes in the memory will exactly fit the process’s memory requirement. Hence, a new hole of smaller size will be created if allocation is made in any of the existing holes. Which one of the following statements is TRUE?
The hole created by worst fit is always larger than the hole created by first fit. | |
The hole created by best fit is never larger than the hole created by first fit.
| |
The hole created by first fit is always larger than the hole created by next fit. | |
The hole created by next fit is never larger than the hole created by best fit. |
Question 5 |
Consider a paging system that uses a 1-level page table residing in main memory and a TLB for address translation. Each main memory access takes 100 ns and TLB lookup takes 20 ns. Each page transfer to/from the disk takes 5000 ns. Assume that the TLB hit ratio is 95%, page fault rate is 10%. Assume that for 20% of the total page faults, a dirty page has to be written back to disk before the required page is read in from disk. TLB update time is negligible. The average memory access time in ns (round off to 1 decimal places) is ______.
154.5 ns |
T=20ns
D=5000ns
h=0.95
p=0.1, 1-p=0.9
d=0.2, 1-d=0.8
EMAT = h×(T+M)+(1-h)[(1-p)×2M+p[(1-d)[D+M]+d(2D+M)]+T]
= 0.95×(20+100)+(1-0.95)[(1-0.1)×200+(0.1)[(1-0.2)[5000+100]+(0.2)(10000+100)]+20]
= 154.5 ns
Question 6 |
A certain moving arm disk storage, with one head, has the following specifications.
Number of tracks/recording surface = 200 Disk rotation speed = 2400 rpm Track storage capacity = 62,500 bits
The average latency of this device is P msec and the data transfer rate is Q bits/sec.
Write the value of P and Q.
P = 12.5, Q = 2.5×106 |
So, in DOS, the disk rotates 2400 times.
Average latency is the time for half a rotation
= 0.5×60/2400 s
= 12.5 ms
In one full rotation, entire data in a track can be transferred. Track storage capacity = 62500 bits
So, disk transfer rate
= 62500 × 2400/60
= 2.5 × 106 bps
So,
P = 12.5, Q = 2.5×106
Question 7 |
(a) The access times of the main memory and the Cache memory, in a computer system, are 500 n sec and 50 n sec, respectively. It is estimated that 80% of the main memory request are for read the rest for write. The hit ratio for the read access only is 0.9 and a write-through policy (where both main and cache memories are updated simultaneously) is used. Determine the average time of the main memory.
(b) Three devices A, B and C are corrected to the bus of a computer, input/output transfers for all three devices use interrupt control. Three interrupt request lines INTR1, INTR2 and INTR3 are available with priority of INTR1 > priority of INTR2 > priority of INTR3.
Draw a schematic of the priority logic, using an interrupt mask register, in which Priority of A > Priority of B > Priority of C.
Theory Explanation. |
Question 8 |
Page size has no impact on internal fragmentation. | |
Multilevel paging is necessary to support pages of different sizes. | |
Paging incurs memory overheads. | |
Paging helps solve the issue of external fragmentation. |
- False, Large page size may lead to higher internal fragmentation.
- False, To support pages of different sizes, the Instruction set architecture should support it. Multi-level paging is not necessary.
- True, The page table has to be stored in main memory, which is an overhead.
- True, Paging avoids the external fragmentation.
Question 9 |
Which one of the following is NOT shared by the threads of the same process?
Stack | |
Address Space | |
File Descriptor Table | |
Message Queue |
Question 10 |
Consider a pipeline processor with 4 stages S1 to S4. We want to execute the following loop:
For(i=1:i<=1000; i++)
{I1,I2,I3,I4}
where the time taken (in ns) by instructions I1 to I4 for stages S1 to S4 are given below:
S1 S2 S3 S4 I1: 1 2 1 2 I2: 2 1 2 1 I3: 1 1 2 1 I4: 2 1 2 1The output of I1 for i=2 will be available after
11 ns | |
12 ns | |
13 ns | |
28 ns |
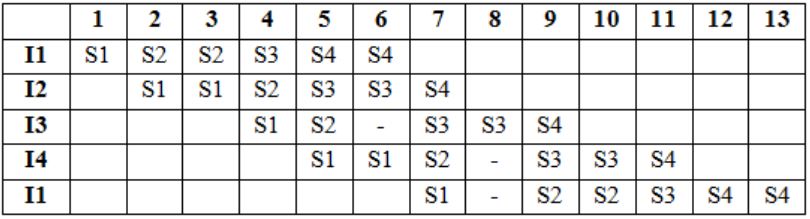
So, total time would be 13 ns.
Question 11 |
The storage area of a disk has innermost diameter of 10 cm and outermost diameter of 20 cm. The maximum storage density of the disk is 1400 bits/cm. The disk rotates at a speed of 4200 RPM. The main memory of a computer has 64-bit word length and 1µs cycle time. If cycle stealing is used for data transfer from the disk, the percentage of memory cycles stolen for transferring one word is
0.5% | |
1% | |
5% | |
10% |
x μs is data transfer time.
% of time CPU idle is,
y/x × 100
Maximum storage density is given, so consider innermost track to get the capacity
= 2 × 3.14 × 5 × 1700 bits
= 3.14 × 14000 bits
Rotational latency = 60/4200 s = 1/70 s
Therefore, to read 64 bits, time required
(106 × 64)/(70 × 3.14 × 17000) μs = 20.8 μs
As memory cycle time given is 1μs,
Therefore, % CPU cycle stolen = (1/20.8) × 100 ≈ 5%
Question 12 |
A disk has 200 tracks (numbered 0 through 199). At a given time, it was servicing the request of reading data from track 120, and at the previous request, service was for track 90. The pending requests (in order of their arrival) are for track numbers
30 70 115 130 110 80 20 25How many times will the head change its direction for the disk scheduling policies SSTF(Shortest Seek Time First) and FCFS (First Come Fist Serve)
2 and 3 | |
3 and 3 | |
3 and 4 | |
4 and 4 |
Direction changes at 120, 110, 130.
FCFS: (90) 120 30 70 115 130 110 80 20 25
Direction changes at 120, 30, 130, 20.
Question 13 |
Consider a 2-way set associative cache memory with 4 sets and total 8 cache blocks (0-7) and a main memory with 128 blocks (0-127). What memory blocks will be present in the cache after the following sequence of memory block references if LRU policy is used for cache block replacement. Assuming that initially the cache did not have any memory block from the current job?
0 5 3 9 7 0 16 55
0 3 5 7 16 55 | |
0 3 5 7 9 16 55 | |
0 5 7 9 16 55 | |
3 5 7 9 16 55 |
So,

Since, each set has only 2 places, 3 will be thrown out as its the least recently used block. So final content of cache will be
0 5 7 9 16 55
Hence, answer is (C).
Question 14 |
A disk has 8 equidistant tracks. The diameters of the innermost and outermost tracks are 1 cm and 8 cm respectively. The innermost track has a storage capacity of 10 MB.
What is the total amount of data that can be stored on the disk if it is used with a drive that rotates it with (i) Constant Linear Velocity (ii) Constant Angular Velocity?
(i) 80 MB (ii) 2040 MB | |
(i) 2040 MB (ii) 80 MB | |
(i) 80 MB (ii) 360 MB | |
(i) 80 MB (ii) 360 MB |
Diameter of inner track = d = 1 cm
Circumference of inner track
= 2 * 3.14 * d/2
= 3.14 cm
Storage capacity = 10 MB (given)
Circumference of all equidistant tracks
= 2 * 3.14 * (0.5+1+1.5+2+2.5+3+3.5+4)
= 113.14 cm
Here, 3.14 cm holds 10 MB
Therefore, 1 cm holds 3.18 MB.
So, 113.14 cm holds
113.14 * 3.18 = 360 MB
So, total amount of data that can be hold on the disk = 360 MB.
For constant angular velocity:
In case of CAV, the disk rotates at a constant angular speed. Same rotation time is taken by all the tracks.
Total amount of data that can be stored on the disk
= 8 * 10 = 80 MB
Question 15 |
A disk has 8 equidistant tracks. The diameters of the innermost and outermost tracks are 1 cm and 8 cm respectively. The innermost track has a storage capacity of 10 MB.
If the disk has 20 sectors per track and is currently at the end of the 5th sector of the inner-most track and the head can move at a speed of 10 meters/sec and it is rotating at constant angular velocity of 6000 RPM, how much time will it take to read 1 MB contiguous data starting from the sector 4 of the outer-most track?
13.5 ms | |
10 ms | |
9.5 ms | |
20 ms |
So, the header has to seek (4 - 0.5) = 3.5cm.
For 10m ------- 1s
1m ------- 1/10 s
100cm ------- 1/(10×100) s
3.5cm ------- 3.5/1000 s = 3.5ms
So, the header will take 3.5ms.
Now, angular velocity is constant and header is now at end of 5th sector. To start from front of 4th sector it must rotate upto 18 sector.
6000 rotation in 60000ms.
1 rotation in 10ms (time to traverse 20 sectors).
So, to traverse 18 sectors, it takes 9ms.
In 10ms, 10MB data is read.
So, 1MB data can be read in 1ms.
∴ Total time = 1+9+3.5 = 13.5ms
Question 16 |
6596 | |
Question 17 |
Consider six memory partitions of sizes 200 KB, 400 KB, 600 KB, 500 KB, 300 KB and 250 KB, where KB refers to kilobyte. These partitions need to be allotted to four processes of sizes 357 KB, 210KB, 468 KB and 491 KB in that order. If the best fit algorithm is used, which partitions are NOT allotted to any process?
200KBand 300 KB | |
200KBand 250 KB | |
250KBand 300 KB | |
300KBand 400 KB |
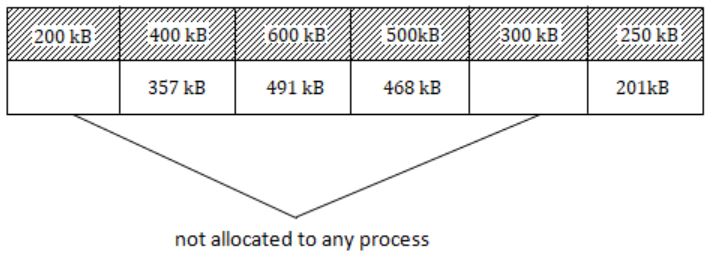
Since Best fit algorithm is used. So, process of size,
357KB will occupy 400KB
210KB will occupy 250KB
468KB will occupy 500KB
491KB will occupy 600KB
So, partitions 200KB and 300KB are NOT alloted to any process.
Question 18 |
2 | |
4 | |
8 | |
16 |
Question 19 |
Assume that in a certain computer, the virtual addresses are 64 bits long and the physical addresses are 48 bits long. The memory is word addressable. The page size is 8 kB and the word size is 4 bytes. The Translation Look-aside Buffer (TLB) in the address translation path has 128 valid entries. At most how many distinct virtual addresses can be translated without any TLB miss?
8×220 | |
4×220 | |
16×210 | |
256×210 |
So, it can refer to 27 pages.
Each page size is 8 kB & word is 4 bytes.
So, the total addresses of virtual address spaces that can be addressed

Question 20 |
Let the page fault service time to 10 ms in a computer with average memory access time being 20 ns. If one page fault is generated for every 106 memory accesses, what is the effective access time for the memory?
21 ns | |
30 ns | |
23 ns | |
35 ns |
EA = p × page fault service time + (1 – p) × Memory access time
= 1/106×10×10
Question 21 |
A computer uses 46-bit virtual address, 32-bit physical address, and a three-level paged page table organization. The page table base register stores the base address of the first-level table (T1), which occupies exactly one page. Each entry of T1 stores the base address of a page of the second-level table (T2). Each entry of T2 stores the base address of a page of the third-level table (T3). Each entry of T3 stores a page table entry (PTE). The PTE is 32 bits in size. The processor used in the computer has a 1 MB 16-way set associative virtually indexed physically tagged cache. The cache block size is 64 bytes.
What is the size of a page in KB in this computer?
2 | |
4 | |
8 | |
16 |
So the no. of entries in one page is 2p/4, where 4 is the page table entry size given in question.
So we know that process size or virtual address space size is equal to
No. of entries × Page size
So total no. of entries for 3 level page table is,
(2p/4)×(2p/4)×(2p/4)
So, No. of entries × Page size = VAS
(2p/4)×(2p/4)×(2p/4)× (2p) = 246
24p = 252
4p = 52
p = 13
∴ Page size = 213
Question 22 |
A computer uses 46-bit virtual address, 32-bit physical address, and a three-level paged page table organization. The page table base register stores the base address of the first-level table (T1), which occupies exactly one page. Each entry of T1 stores the base address of a page of the second-level table (T2). Each entry of T2 stores the base address of a page of the third-level table (T3). Each entry of T3 stores a page table entry (PTE). The PTE is 32 bits in size. The processor used in the computer has a 1 MB 16-way set associative virtually indexed physically tagged cache. The cache block size is 64 bytes.
What is the minimum number of page colours needed to guarantee that no two synonyms map to different sets in the processor cache of this computer?
2 | |
4 | |
8 | |
16 |
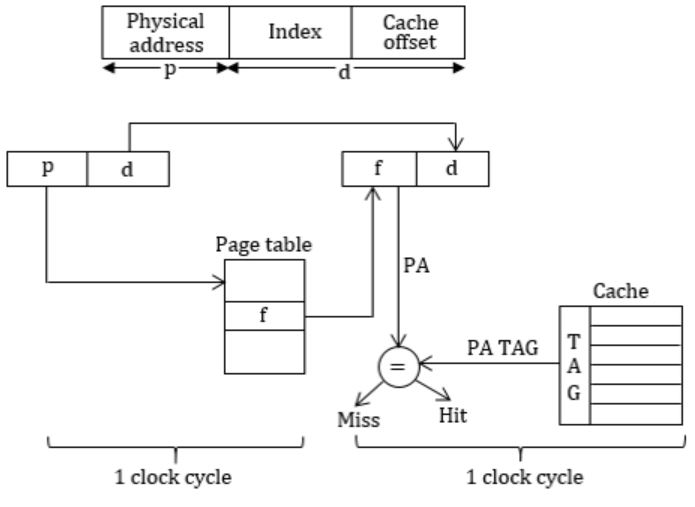
Architecture of virtual indexed physically tagged (VIPT):
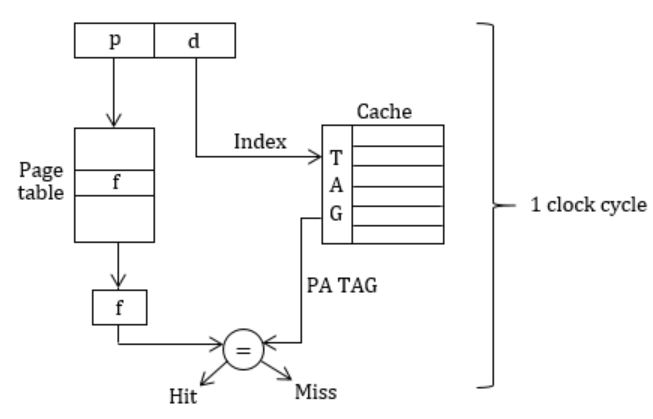
VIPT cache and aliasing effect and synonym.
Alias: Same physical address can be mapped to multiple virtual addresses.
Synonym: Different virtual addresses mapped to same physical address (for data sharing).
So these synonyms should be in same set to avoid write-update problems.
In our problem VA = 46bits

We are using 16bits for indexing into cache.
To have two synonym is same set we need to have same 16 bits index for PA & VA.
Assume that physical pages are colored and each set should have pages of same color so that any synonyms are in same set.
Since page size = 8KB ⇒ 13bits
These 13bits are not translated during VA→PA. So 13bits are same out of 16 Index bits, 13 are same we need to make 3bits (16-13) same now.
3bits can produce, 23 = 8 combinations which can be mapped on the different sets, so we need 8 different colors to color our pages. >br> In physically indexed cache indexing is done via physical address bits, but in virtual indexed cache, cache is indexed from (offset + set) bits. In physical Index cache indexing is done one to one (1 index maps to one page in one block of cache). In VIPT we have more/ extra bits, so mapping is not one-one. Hence these extra bits have to be taken care, such that if two virtual address refers to same page in cache block of different sets then they have to be assumed same i.e., we say of same color and put same color page in one set to avoid write update problems.
Question 23 |
Consider a paging hardware with a TLB. Assume that the entire page table and all the pages are in the physical memory. It takes 10 milliseconds to search the TLB and 80 milliseconds to access the physical memory. If the TLB hit ratio is 0.6, the effective memory access time (in milliseconds) is _________.
122 | |
123 | |
124 | |
125 |
= 10 + 0.4 × 80 + 80
= 10 + 32 + 80
= 122 ms
Question 24 |
The memory access time is 1 nanosecond for a read operation with a hit in cache, 5 nanoseconds for a read operation with a miss in cache, 2 nanoseconds for a write operation with a hit in cache and 10 nanoseconds for a write operation with a miss in cache. Execution of a sequence of instructions involves 100 instruction fetch operations, 60 memory operand read operations and 40 memory operand write operations. The cache hit-ratio is 0.9. The average memory access time (in nanoseconds) in executing the sequence of instructions is __________.
1.68 | |
1.69 | |
1.70 | |
1.71 |
= 200 instructions (operations)
Time taken for fetching 100 instructions (equivalent to read) = 90*1ns + 10*5ns = 140ns
Memory operand Read operations = 90% (60)*1ns + 10% (60) × 5ns = 54ns + 30 ns = 84ns
Memory operands Write operations time = 90% (40)*2ns + 10% (40)*10ns
= 72ns + 40ns = 112ns
Total time taken for executing 200 instructions = 140 + 84 + 112 = 336ns
∴ Average memory access time = 336 ns/200 = 1.68ns
Question 25 |
64 MB | |
16 MB | |
1 GB
| |
4 GB |
Question 26 |
A technique for overcoming internal fragmentation | |
A paging technique | |
A technique for overcoming external fragmentation | |
A technique for compressing the data |
Question 27 |
They run at different time instants and not in parallel | |
They are in different logical addresses | |
They use a protection algorithm in the scheduler | |
Every address generated by the CPU is being checked against the relocation and limit parameters |
Question 28 |
estimating process-wise demand for frames using working set model and limiting the total demand
| |
controlling the page fault frequency within safe range by adjusting degree of multi-programming | |
Banker’s Algorithm | |
estimating process-wise demand for frames using working set model and limiting the total demand and controlling the page fault frequency within safe range by adjusting degree of multi-programming but not Banker’s Algorithm |
Question 29 |
Dynamic storage allocation | |
Disk space compaction | |
File Allocation Table | |
garbage collection |
Question 30 |
If the executing program size is greater than the existing RAM of a computer, it is still possible to execute the program, if the OS supports
Synchronization
| |
fault tolerance | |
paging system | |
Scheduling |
Question 31 |
Variable partition memory management technique with compaction results in
reduction of fragmentation | |
minimal wastage | |
segment sharing | |
None of the given options |
Question 32 |
The working set model is used in memory management to implement the concept of:
Principle of locality
| |
Thrashing
| |
Paging
| |
Segmentation
|
Or
The working set is the memory that's being accessed "frequently" by an application or set of applications.
Principle of Locality does the same thing as explained above.
In computer science, locality of reference, also known as the principle of locality, is the tendency of a processor to access the same set of memory locations repetitively over a short period of time.There are two basic types of reference locality – temporal and spatial locality. Temporal locality refers to the reuse of specific data, and/or resources, within a relatively small time duration. Spatial locality (also termed data locality) refers to the use of data elements within relatively close storage locations.
Question 33 |
Page fault occurs when
The page is an main memory
| |
The page has an address, which cannot be loaded
| |
The page is not in main memory | |
The page is not in cache memory |
Question 34 |
Consider a system with page fault service time(S)=100 ns, main memory access time(M)=20 ns, and page fault rate(P)=65%. Calculate the effective memory access time.
62 ns | |
82 ns
| |
80 ns
| |
72 ns
|
EMAT = (1 - p) × M + p・S
= 0.35 × 20 + 0.65 × 100
= 7 + 65
= 72 ns
Question 35 |
It is based on a linear logical memory addressing concept. | |
Entire program need not be loaded into memory before execution | |
It suffers from both internal and external fragmentations | |
Page table is not required once a program is loaded |
Question 36 |
Sequential Consistency | |
General Consistency | |
Strict Consistency | |
Weak Consistency | |
Update it |
Question 37 |
Object Code | |
Relocation Bits | |
Names and locations of all external symbols defined in the object module | |
Absolute address of internal symbols |
Question 38 |
A mechanism used by OS to boost its performance | |
A phenomenon where CPU utilization is very poor | |
A concept to improve CPU utilization | |
None |
