topic - solutions adda

Minimum-Spanning-Tree

Please wait while the activity loads.
If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.

If loading fails, click here to try again

Question 1

Let G be a connected undirected weighted graph. Consider the following two statements.
S₁: There exists a minimum weighted edge in G which is present in every minimum spanning tree of G.
S₂:If every edge in G has distinct weight, then G has a unique minimum spanning tree.
Which of the following options is correct?

A	S₁is false and S₂is true.
B	S₁is true and S₂is false.
C	Both S₁ and S₂are false.
D	Both S₁ and S₂are true.

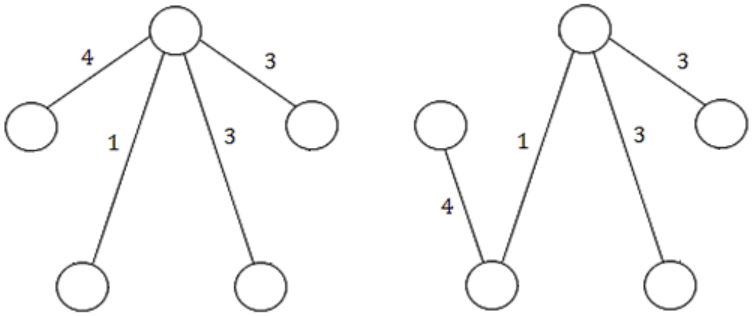
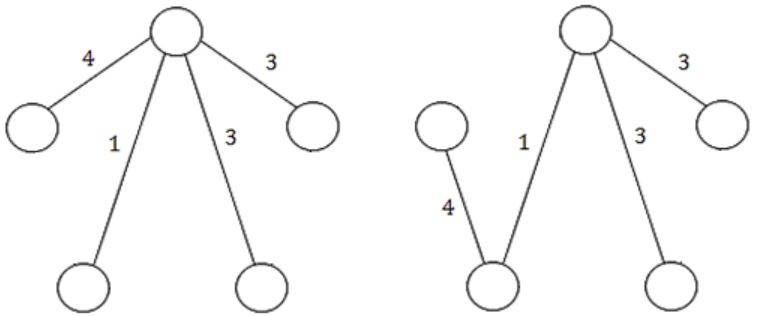
AlgorithmsMinimum-Spanning-TreeGATE 2021 CS-Set-2Video-Explanation

Question 1 Explanation:

Statement-1: FALSE: The given statement is not valid for all the cases because they are not mentioned, edge weights are in distinct or duplicate. So, we can take any random edge weights for the given statement.

Example:

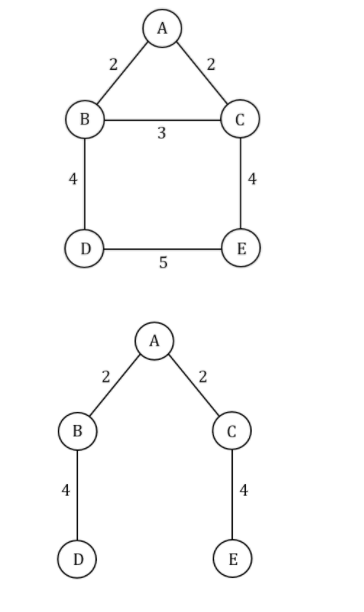
Statement-2: TRUE: Using the kruskal’s (or) prim's algorithm we get a unique MST when there is a unique edge weight.

Example:

Based on the above graph, we get the MST is

Question 2

In a directed acyclic graph with a source vertex s, the quality-score of s directed path is defined to be the product of the weights of the edges on the path. Further, for a vertex v other than s, the quality-score of v is defined to be the maximum among the quality-scores of all the paths from s to v. The quality-score of s is assumed to be 1.

The sum of the quality-scores of all the vertices in the graph shown above is _________.

929

AlgorithmsMinimum-Spanning-TreeGATE 2021 CS-Set-2Video-Explanation

Question 3

How many minimum spanning trees does the following graph have? Draw them. (Weights are assigned to the edge).

A	Theory Explanation.

AlgorithmsMinimum-Spanning-TreeGATE 1995

Question 4

Let G = (V,E) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighted edge (u,v) ∈ V×V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is

A	θ(\|E\|+\|V\|)
B	θ(\|E\| log\|V\|)
C	θ(\|E\|\|V\|)
D	θ(\|V\|)

AlgorithmsMinimum-Spanning-TreeGATE 2020Video-Explanation

Question 4 Explanation:

Method-1:
• As T is a minimum spanning tree and we need to add a new edge to existing spanning tree.
• Later we need to check still T is a minimum spanning tree or not, So we need to check all vertices whether there is any cycle present after adding a new edge.
• All vertices need to traverse to confirm minimum spanning tree after adding new edge then time complexity is O(V).
Method-2:
Time Complexity:
Total vertices: V, Total Edges : E
• O(logV) – to extract each vertex from the queue. So for V vertices – O(VlogV)
• O(logV) – each time a new pair object with a new key value of a vertex and will be done at most once for each edge. So for total E edge – O(ElogV)
• So overall complexity: O(VlogV) + O(ElogV) = O((E+V)logV) = O(ElogV)
Note: Method-1 is the most appropriate answer for giving a question.

Question 5

Consider a graph G = (V, E), where V = {v₁, v₂, …, v₁₀₀}, E = {(v_i, v_j) | 1 ≤ i < j ≤ 100}, and weight of the edge (v_i, v_j) is |i - j|. The weight of the minimum spanning tree of G is ______.

AlgorithmsMinimum-Spanning-TreeGATE 2020Video-Explanation

Question 5 Explanation:

• If there are n vertices in the graph, then each spanning tree has n − 1 edges.
• N =100
• Edge weight is |i-j| for Edge (vi,vj) {1<=i<=100}
• The weight of edge(v1,v2) is 1 , edge(v5,v6) is 1.
• So, 99 edges of weight is 99.

Question 6

A complete, undirected, weighted graph G is given on the vertex {0, 1,...., n−1} for any fixed ‘n’. Draw the minimum spanning tree of G if
(a) the weight of the edge (u,v) is ∣u − v∣
(b) the weight of the edge (u,v) is u + v

A	Theory Explanation.

AlgorithmsMinimum-Spanning-TreeGATE 1996

Question 7

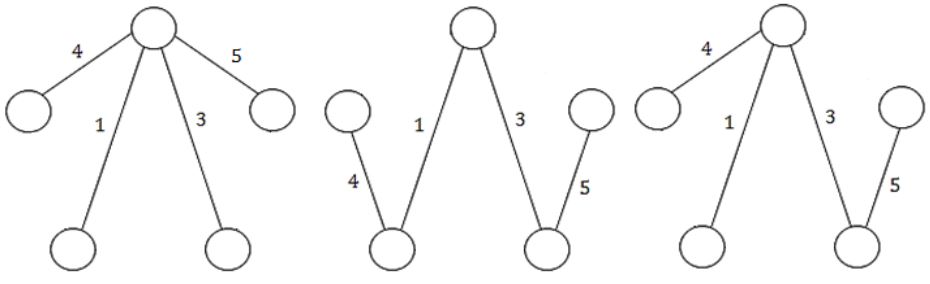
Consider the following undirected graph G:

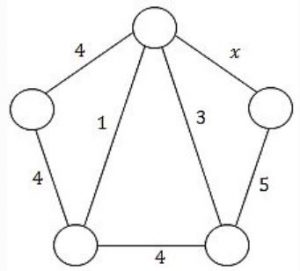
Choose a value for x that will maximize the number of minimum weight spanning trees (MWSTs) of G. The number of MWSTs of G for this value of x is _________.

A	4
B	5
C	6
D	7

AlgorithmsMinimum-Spanning-TreeGATE 2018Video-Explanation

Question 7 Explanation:

Here, x = 5 because it is having maximum number of spanning trees.
If x = 5 then the total number of MWSTs are 4.
If r = 1

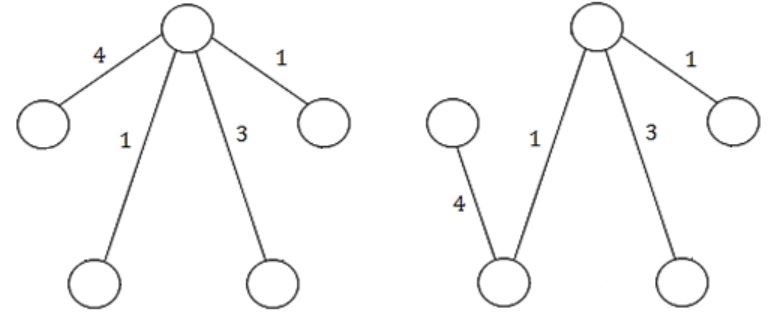
If r = 2

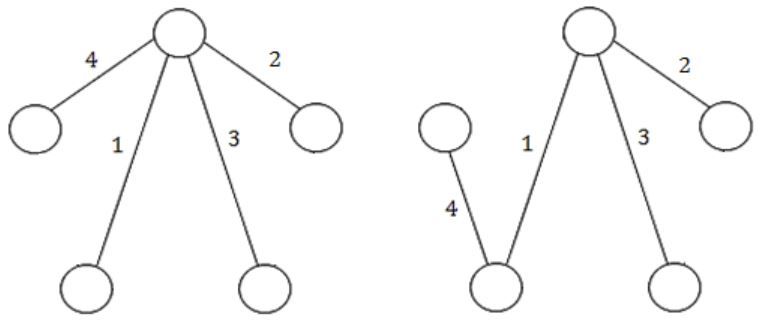
If r = 3

If r = 4

If r = 5

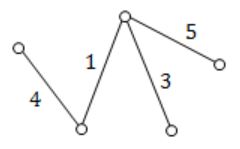
Question 8

Let G be an undirected connected graph with distinct edge weight. Let e_max be the edge with maximum weight and e_min the edge with minimum weight. Which of the following statements is false?

A	Every minimum spanning tree of G must contain e_min
B	If e_max is in a minimum spanning tree, then its removal must disconnect G
C	No minimum spanning tree contains e_max
D	G has a unique minimum spanning tree

AlgorithmsMinimum-Spanning-TreeGATE 2000

Question 8 Explanation:

Minimum Spanning Tree:

Question 9

Consider a weighted undirected graph with vertex set V = {n1,n2,n3,n4,n5,n6} and edge set

 E = {(n1,n2,2),(n1,n3,8),(n1,n6,3),(n2,n4,4),(n2,n5,12),(n3,n4,7),(n4,n5,9), 
     (n4,n6,4)}. The third value in each tuple represents the weight of the edge 
     specified in the tuple.

(a) List the edges of a minimum spanning tree of the graph.
(b) How many distinct minimum spanning trees does this graph have?
(c) Is the minimum among the edge weights of a minimum spanning tree unique overall possible minimum spanning trees of a graph?
(d) Is the maximum among the edge weights of a minimum spanning tree unique over all possible minimum spanning trees of a graph?

A	Theory Explanation is given below.

AlgorithmsMinimum-Spanning-TreeGATE 2001

Question 9 Explanation:

(b) 2 distinct MST's.
(c) Yes, it always. Because 'the edge weight 2 is unique'.
(d) Yes, it always. Because 'the edge weight 9 is unique'.

Question 10

What is the weight of a minimum spanning tree of the following graph ?

A	29
B	31
C	38
D	41

AlgorithmsMinimum-Spanning-TreeGATE 2003

Question 10 Explanation:

1+2+3+2+8+4+4+2+5 =31

Question 11

Consider a simple undirected weighted graph G , all of whose edge weights are distinct. Which of the following statements about the minimum spanning trees of G is/are TRUE?

A	The edge with the second smallest weight is always part of any minimum spanning tree of G .
B	One or both of the edges with the third smallest and the fourth smallest weights are part of any minimum spanning tree of G .
C
D	G can have multiple minimum spanning trees.

AlgorithmsMinimum-Spanning-TreeGATE 2022Video-Explanation

Question 11 Explanation:

Let assume the graph and minimum spanning tree of the corresponding graph.

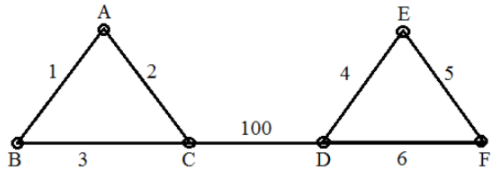
Option-A: TRUE: As per the above graph, the second minimum edge weight is also part of the MST.
The second smallest weight is always in MST because it will not form a cycle.
Option-B: TRUE: Graph G is having more than 4 vertices. Suppose 3rd smallest element is forming a cycle then it takes 4th smallest element. So, the given statement is TRUE.
Option-C: TRUE: As per the example graph, it is always correct.
Option-D: FALSE: We will get a unique minimum spanning tree if edge weights are distinct.

Question 12

Let G ( V , E ) be a directed graph, where V = {1, 2,3, 4, 5} is the set of vertices and E is the set of directed edges, as defined by the following adjacency matrix A .

AlgorithmsMinimum-Spanning-TreeGATE 2022Video-Explanation

Question 12 Explanation:

Graph have 2 elements --> We get 1 MST
Graph have 3 elements --> We get 2 MSTs
Graph have 4 elements --> We get 6 MSTs (3*2*1)
Graph have 5 elements --> We get 24 MSTs(4*3*2*1)

There are 12 questions to complete.

Access quiz wise question and answers by becoming as a solutions adda PRO SUBSCRIBER with Ad-Free content

If you have registered and made your payment please contact solutionsadda.in@gmail.com to get access

A	θ(\|E\|+\|V\|)
B	θ(\|E\| log\|V\|)
C	θ(\|E\|\|V\|)
D	θ(\|V\|)