Prefix-Postfix-Expression
Question 1 |
The postfix expression for the infix expression
A + B*(C + D)/F + D*E is:
AB + CD + *F/D + E* | |
ABCD + *F/DE*++ | |
A *B + CD/F *DE++ | |
A + *BCD/F* DE++ | |
None of the above |
Question 1 Explanation:
The postfix expression will be,
A B C D + * F / + D E * +
A B C D + * F / + D E * +
Question 2 |
The result evaluating the postfix expression 10 5 + 60 6 / * 8 - is
284 | |
213 | |
142 | |
71 |
Question 2 Explanation:
→ '10' is pushed in the stack
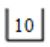
→ '5' is pushed in the stack

→ '+' comes so addition will be done by popping the top two elements in the stackand the result is pushed back into the stack, i.e., 10+5 = 15
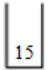
→ 60 pushed in the stack
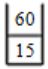
→ 6 pushed in the stack

→ '/' comes. So, 60/6 = 10

→ '*' comes. So, 15 * 10 = 150
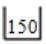
→ '8' comes, push in the stack
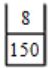
→ '-' comes. So, 150-8 = 142

So the final result is 142.
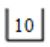
→ '5' is pushed in the stack

→ '+' comes so addition will be done by popping the top two elements in the stackand the result is pushed back into the stack, i.e., 10+5 = 15
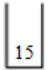
→ 60 pushed in the stack

→ 6 pushed in the stack

→ '/' comes. So, 60/6 = 10

→ '*' comes. So, 15 * 10 = 150
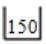
→ '8' comes, push in the stack

→ '-' comes. So, 150-8 = 142

So the final result is 142.
Question 3 |
The prefix equivalent of the following infix expression is:
a / b - c + d * e - a * c
- + - / a b c * d e * a c | |
+ - - / a b c * d e * a c | |
- + / a b c - * d e * a c | |
- - + / a b c * d e * a c |
Question 3 Explanation:
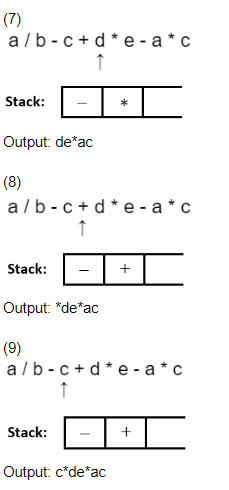
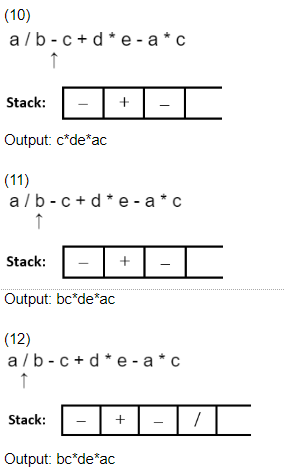
a / b - c + d * e - a * c
* Start scanning the expression from RHS. * Push the operators on the top of the stack by ensuring that only high priority operator can be pushed over a low priority operator.
* If a low priority operator is encountered in expression while scanning it, and if top of stack have high priority operator then pop it and after that push low priority operator on top of stack.
* Print each operand just after scanning it.



* Start scanning the expression from RHS. * Push the operators on the top of the stack by ensuring that only high priority operator can be pushed over a low priority operator.
* If a low priority operator is encountered in expression while scanning it, and if top of stack have high priority operator then pop it and after that push low priority operator on top of stack.
* Print each operand just after scanning it.





Question 4 |
Convert the prefix expression to infix
-*+ABC*-DE+FG
-*+ABC*-DE+FG
(A-B)*C+(D*E)-(F+G) | |
(A+B)*C-(D-E)*(F-G) | |
(A+B-C)*(D-E)*(F+G) | |
(A+B)*C-(D*E)-(F+G) | |
None of the above |
Question 4 Explanation:
Prefix: -*+ABC*-DE+FG
Read the Prefix expression in reverse order (from right to left)
GF+ED-*CBA+*-
If the symbol is an operand, then push it onto the Stack
If the symbol is an operator, then pop two operands from the Stack
Create a string by concatenating the two operands and the operator between them.
string = (operand1 + operator + operand2)
And push the resultant string back to Stack
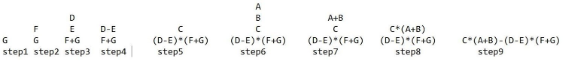
=>
C*(A+B)-(D-E)*(F+G)
which is equivalent to =>
(A+B)*C-(D-E)*(F+G)
Read the Prefix expression in reverse order (from right to left)
GF+ED-*CBA+*-
If the symbol is an operand, then push it onto the Stack
If the symbol is an operator, then pop two operands from the Stack
Create a string by concatenating the two operands and the operator between them.
string = (operand1 + operator + operand2)
And push the resultant string back to Stack
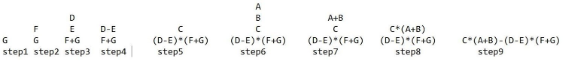
=>
C*(A+B)-(D-E)*(F+G)
which is equivalent to =>
(A+B)*C-(D-E)*(F+G)
Question 5 |
The value of the postfix expression abc*de+/- where a=20, b=3, c=4, d=1 and e=5 is
134 | |
-22 | |
48 | |
18 |
Question 5 Explanation:
Here we will start traversing the expression from left to right and if an operand is encountered then it will be pushed on the top of stack and if an operator is encountered then top two elements will be popped off from the top of stack and current operator is applied on those two operands and then in the end the result of operation will be pushed back on the top of stack. This procedure continues till the whole expression is traversed.
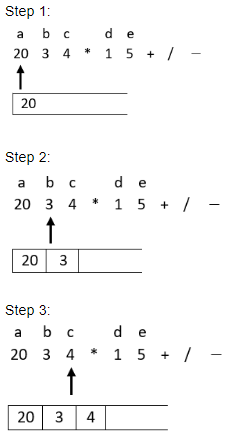

Step: 7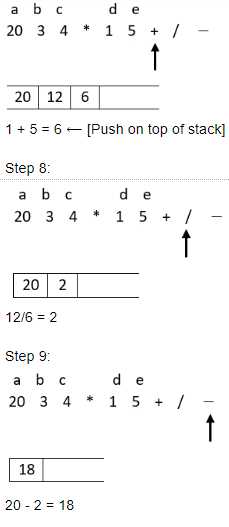
Hence option 4 is the correct answer.


Step: 7

Hence option 4 is the correct answer.
There are 5 questions to complete.
