Propositional-Logic
Question 1 |
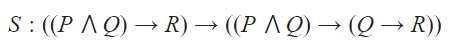
S is a contradiction. | |
The anecdote of S is logically equivalent to the consequent of S. | |
S is a tautology. | |
S is neither a tautology nor a contradiction. |
Question 2 |
Obtain the principal (canonical) conjunctive normal form of the propositional formula
(p ∧ q) V (¬q ∧ r)
Where ‘∧’ is logical and, ‘v’ is inclusive or and ¬ is negation.
Theory Explanation. |
Question 3 |
Which one of the following predicate formulae is NOT logically valid?
Note that W is a predicate formula without any free occurrence of x.
∃x(p(x) → W) ≡ ∀x p(x) → W | |
∀x(p(x) → W) ≡ ∀x p(x) → W
| |
∃x(p(x) ∧ W) ≡ ∃x p(x) ∧ W | |
∀x(p(x) ∨ W) ≡ ∀x p(x) ∨ W |
~p→q ≡ ~p∨q
Demorgan laws:
~(∀x(a(x)) ≡ ∃x~a(x)
~(∃x(a(x)) ≡ ∀x~a(x)
(A) ∃x(p(x)→w) ≡ ∀x p(x)→w
LHS: ∃x(p(x)→w) ≡ ∃x(~p(x)∨w)
≡ ∃x(~p(x))∨w
Demorgan’s law:
~(∀x(a(x)) = ∃x ~ a(x)
≡ ~(∀x P(x)) ∨ w
≡ (∀x) P(x) → w ≡ RHS
It’s valid.
(B) ∀x(P(x) → w) ≡ ∀x(~P(x) ∨ w)
≡ ∀x(~P(x)) ∨ w
≡ ~(∃x P(x)) ∨ w
≡ ∃x P(x) → w
This is not equal to RHS.
(C) ∃x(P(x) ∧ w) ≡ ∃x P(x) ∧ w
‘w’ is not a term which contains x.
So the quantifier does not have any impact on ‘w’.
Thus it can be written as
∃x(P(x)) ∧ w) ≡ ∃x P(x) ∧ w
(D) ∀(x)(P(x) ∨ w) ≡ ∀x P(x) ∨ w
‘w’ is not a term which contains ‘x’.
So the quantifier does not have an impact on ‘w’.
Thus ∀(x)(P(x) ∨ w) ≡ ∀x P(x) ∨ w
Question 4 |
Which of the following is false? Read ∧ as AND, ∨ as OR, ~ as NOT, → as one way implication and ↔ as two way implication.
((x → y) ∧ x) → y | |
((x → y) ∧ (x ∧ y)) → x | |
(x → (x ∨ ψ)) | |
((x ∨ y) ↔ (x → y) |
then option (D) will be False.
Question 5 |
Which of the following propositions is a tautology?
(p ∨ q) → p | |
p ∨ (q → p) | |
p ∨ (p → q) | |
p → (p → q) |

Question 6 |
φ ≡ ∃s∃t∃u∀v∀w∀x∀y ψ(s,t,u,v,w,x,y)
where ψ(s,t,u,v,w,x,y) is a quantifier-free first-order logic formula using only predicate symbols, and possibly equality, but no function symbols. Suppose φ has a model with a universe containing 7 elements.
Which one of the following statements is necessarily true?
There exists at least one model of φ with universe of size less than or equal to 3. | |
There exists no model of φ with universe of size less than or equal to 3.
| |
There exists no model of φ with universe of size greater than 7. | |
Every model of φ has a universe of size equal to 7. |
"∃" there exists quantifier decides whether a sentence belong to the model or not.
i.e., ~∃ will make it not belong to the model. (1) We have ‘7’ elements in the universe, So max. size of universe in a model = ‘7’
(2) There are three '∃' quantifiers, which makes that a model have atleast “3” elements. So, min. size of universe in model = ‘7’.
(A) is False because: (2)
(B) is true
(C) is false because of (1)
(D) is false, because these all models with size {3 to 7} not only ‘7’.
Question 7 |
What is the converse of the following assertion?
I stay only if you go.
I stay if you go | |
If I stay then you go | |
If you do not go then I do not stay | |
If I do not stay then you go |
⇒ i.e., A→B
Where A = If I stay; B = you go
Converse for (A→B) is (B→A)
⇒ If you go then I stay.
Question 8 |
(a) Show that the formula [(~p ∨ q) ⇒ (q ⇒ p)] is not a tautology.
(b) Let A be a tautology and B be any other formula. Prove that (A ∨ B) is a tautology.
Theory Explanation. |
Question 9 |
Let a, b, c, d be propositions. Assume that the equivalence a ↔ (b ∨ -b) and b ↔ c hold. Then the truth-value of the formula (a ∧ b) → (a ∧ c) ∨ d is always
True | |
False | |
Same as the truth-value of b | |
Same as the truth-value of d |
Given ⇒ (a∧b) → (a∧c) ∨d
⇒ (a∧b) → (a∧c) ∨d (b⇔c)
⇒ T∨d
⇒ T
Question 10 |
Consider two well-formed formulas in prepositional logic
F1: P ⇒ ¬P F2: (P⇒¬P)∨(¬P⇒P)
Which of the following statements is correct?
F1 is satisfiable, F2 is valid | |
F1 unsatisfiable, F2 is satisfiable | |
F1 is unsatisfiable, F2 is valid | |
F1 and F2 are both satisfiable |

F1 is satisfiable; F2 is valid.
Question 11 |
“If X then Y unless Z” is represented by which of the following formulas in prepositional logic? (“¬“, is negation, “∧” is conjunction, and “→” is implication)
(X∧¬Z)→Y | |
(X∧Y)→¬Z | |
X→(Y∧¬Z) | |
(X→Y)∧¬Z |
⇒ Z ∨ ¬X ∨ Y
⇒ ¬X ∨ Z ∨ Y
Option A:
(X ∧ ¬Z) → Y = ¬(X ∧ ¬Z ) ∨ Y = ¬X ∨ Z ∨ Y Hence, option (A) is correct.
Question 12 |
Which of the following is a valid first order formula? (Here α and β are first order formulae with x as their only free variable)
((∀x)[α] ⇒ (∀x)[β]) ⇒ (∀x)[α⇒β]
| |
(∀x)[α] ⇒ (∃x)[α ∧ β] | |
((∀x)[α ∨ β] ⇒ (∃x)[α] ⇒ (∀x)[α] | |
(∀x)[α ⇒ β] ⇒ ((∀x)[α] ⇒ (∀x)[β]) |
Here, α, β are holding values of x. Then and RHS saying that α holding the value of x and β is holding value of x.
Then LHS ⇒ RHS.
Question 13 |
Consider the following formula a and its two interpretations I1 and I2
α: (∀x)[Px ⇔ (∀y)[Qxy ⇔ ¬Qyy]] ⇒ (∀x)[¬Px]
I1: Domain: the set of natural numbers
Px ≡ 'x is a prime number'
Qxy ≡ 'y divides x'
I2: same as I1 except that Px = 'x is a composite number'.
Which of the following statements is true?
I1 satisfies α, I2 does not | |
I2 satisfies α, I1 does not
| |
Neither I2 nor I1 satisfies α
| |
Both I1 and I2 satisfy α |
(∀x)[Px ⇔ (∀y)[Qxy ⇔ ¬Qyy]] ⇒(∀x)[¬Px]
Qyy is always true, because y divide y, then ¬Qyy is false.
∀x[(P(x) ⇔ ∀y [Qxy ⇔ False]]
∀y [Qxy ⇔ False] can be written as ∀y[¬axy]
⇒(∀x)[P(x) ⇔ ∀y[¬Qxy]]
Here, ¬Qxy says that y doesnot divides x, which is not always be true.
For example, if x=y then it is false then ∀y[¬Qxy] is not true for all values of y.
⇒(∀x)[P(x) ⇔ False]
⇒(∀x)[¬P(x) = RHS]
LHS = RHS
⇒ Irrespective of x, whether x is prime of composite number I1 and I2 satisfies α.
Question 14 |
The following resolution rule is used in logic programming.
Derive clause (P ∨ Q) from clauses (P ∨ R), (Q ∨ ¬R)
Which of the following statements related to this rule is FALSE?
((P ∨ R) ∧ (Q ∨ ¬R)) ⇒ (P ∨ Q) is logically valid | |
(P ∨ Q) ⇒ ((P ∨ R) ∧ (Q ∨ ¬R)) is logically valid
| |
(P ∨ Q) is satisfiable if and only if (P∨R) ∧ (Q∨¬R) is satisfiable | |
(P ∨ Q) ⇒ FALSE if and only if both P and Q are unsatisfiable
|

It is may be True (or) False depending on values. So this is not valid.
Question 15 |
Identify the correct translation into logical notation of the following assertion.
"Some boys in the class are taller than all the girls"
Note: taller(x,y) is true if x is taller than y.
(∃x) (boy(x) → (∀y) (girl(y) ∧ taller(x,y))) | |
(∃x) (boy(x) ∧ (∀y) (girl(y) ∧ taller(x,y))) | |
(∃x) (boy(x) → (∀y) (girl(y) → taller(x,y))) | |
(∃x) (boy(x) ∧ (∀y) (girl(y) → taller(x,y))) |
'∧' → predicts statements are always true, no matter the value of x.
'→' → predicts there is no need of left predicate to be true always, but whenever it becomes true, then right predicate must be true.
Option D:
There exists a some boys who are taller than of all girls y.
Question 16 |
The following propositional statement is (P → (Q v R)) → ((P v Q) → R)
satisfiable but not valid
| |
valid | |
a contradiction | |
None of the above |
If P=T; Q=T; R=T
(P→(T∨T)) → ((T∨T)→R)
(P→T) → (T→R)
(T→T) → (T→T)
T→T
T(Satisfiable)
Question 17 |
(a) Let * be a Boolean operation defined as ![]()
If C = A * B then evaluate and fill in the blanks:
(i) A * A = _______
(ii) C * A = _______
(b) Solve the following boolean equations for the values of A, B and C:
![]()
Theory Explanation. |
Question 18 |
Show that proposition C is a logical consequence of the formula
A ∧ (A →(B ∨ C)) ∧ (B → ~A)
Using truth tables.
Theory Explanation. |
Question 19 |
(a) Uses Modus ponens (A, A →|= B) or resolution to show that the following set is inconsistent:
(1) Q(x) → P(x)V ~ R(a) (2) R(a) ~ Q(a) (3) Q(a) (4) ~ P(y)
Where x and y are universally quantified variables, a is a constant and P, Q, R are monadic predicates.
(b) Let S be the set of all integers and let n > 1 be a fixed integer. Define for a, b ∈ S, a R biff a-b is a multiple of n. Show that R is an equivalence relation and finds its equivalence classes for n = 5.
Theory Explanation. |
Question 20 |

Which one of the following choices is correct?
Both S1and S2 are tautologies. | |
Neither S1and S2 are tautology. | |
S1is not a tautology but S2is a tautology. | |
S1is a tautology but S2is not a tautology. |
A tautology is a formula which is "always true" . That is, it is true for every assignment of truth values to its simple components.
Method 1:
S1: (~p ^ (p Vq)) →q
The implication is false only for T->F condition.
Let's consider q as false, then
(~p ^ (p Vq)) will be (~p ^ (p VF)) = (~p ^ (p)) =F.
It is always F->F which is true for implication. So there are no cases that return false, thus its always True i.e. its Tautology.
S2:
q->(~p (p Vq))
The false case for implication occurs at T->F case.
Let q=T then (~p (p Vq)) = (~p (p VT))= ~p. (It can be false for p=T).
So there is a case which yields T->F = F. Thus its not Valid or Not a Tautology.
Method 2:

Question 21 |
Consider the following first order logic formula in which R is a binary relation symbol.
∀x∀y (R(x, y) => R(y, x))The formula is
satisfiable and valid | |
satisfiable and so is its negation | |
unsatisfiable but its negation is valid | |
satisfiable but its negation is unsatisfiable |
Question 22 |
Which one of these first-order logic formula is valid?
∀x(P(x) ⇒ Q(x)) ⇒ (∀xP(x) ⇒ ∀xQ(x)) | |
∃x(P(x) ∨ Q(x)) ⇒ (∃xP(x) ⇒ ∃xQ(x)) | |
∃x(P(x) ∧ Q(x)) (∃xP(x) ∧ ∃xQ(x)) | |
∀x∃y P(x, y) ⇒ ∃y∀x P(x, y) |
RHS = if P(x) holds for all x, then Q(x) holds for all x
LHS ⇒ RHS (✔)
RHS ⇒ LHS (️×)
Question 23 |
Which of the following first order formula is logically valid? Here α(x) is a first order formula with x as a free variable, and β is a first order formula with no free variable.
[β→(∃x,α(x))]→[∀x,β→α(x)] | |
[∃x,β→α(x)]→[β→(∀x,α(x))] | |
[(∃x,α(x))→β]→[∀x,α(x)→β] | |
[(∀x,α(x))→β]→[∀x,α(x)→β] |
L.H.S. : If there is an x such that α(x) is true, then β is true.
R.H.S. : For all x, if α(x) true, then β is true.
Here, the given LHS and RHS are to be same as β is a formula which can be independent of x (if β is true for one x, it is true for every x, and vice-versa).
Here, LHS = RHS
So, Option C is valid.
Question 24 |
Which of the following is the negation of [∀x, α →(∃y, β →(∀ u, ∃v, y))]
[∃x, α → (∀y, β → (∃u, ∀v, y))] | |
[∃x, α → (∀y, β → (∃u, ∀ v, ¬y))] | |
[∀x, ¬α → (∃y, ¬β → (∀u, ∃v, ¬y))] | |
[∃x, α ʌ (∀y, β ʌ (∃u, ∀v, ¬y))] |
⇔ [∃x, [α × ~(∃y, β → (∀u, ∃v, y))]
⇔ [∃x, [α × ∀y, ~(β → (∀u, ∃v, y)]
⇔ [∃x, [α × ∀y, ~(β × ~(∀u, ∃v, y)]
⇔ [∃x, [α × ∀y(β × (∃u, ∀v, y)]
Question 25 |
Which of the following well-formed formulas are equivalent?
P → Q | |
¬Q → ¬P | |
¬P ∨ Q | |
¬Q → P | |
A, B and C. |
¬Q → ¬P ⇔ Q ∨ ¬P
¬P ∨ Q ⇔ ¬P ∨ Q
¬Q → P ⇔ Q ∨ P
A, B and C are equivalent.
Question 26 |
Choose the correct alternatives (More than one may be correct). Indicate which of the following well-formed formulae are valid:
(P⇒Q) ∧ (Q⇒R) ⇒ (P⇒R) | |
(P⇒Q) ⇒ (¬P⇒¬Q) | |
(P∧(¬P∨¬Q)) ⇒ Q
| |
(P⇒R) ∨ (Q⇒R) ⇒ ((P∨Q)⇒R) |
Since implication A → B is False only when A = T and B = F. So to prove any implication is valid or not try to get
TRUE → FALSE, if we succeed then it is not valid, if we not then well formed formula is valid.
So, for option (A),
Substitute P=T and R=F
RHS:
P→R becomes False.
LHS:
(P→Q) ∧ (P→R)
To get true here we need T∧T. So substitute Q=T which makes P→Q TRUE and P→R FALSE.
So, T∧F = F which makes LHS = False.
Hence, we are unable to get T→F which proves well formed formula given in option (A) is valid.
Similarly, try for (B), (C), (D). We get T → F in these options which says these well formed formula is invalid.
Question 27 |
Let P, Q and R be three atomic prepositional assertions. Let X denote (P ∨ Q) → R and Y denote (P → R) ∨ (Q → R). Which one of the following is a tautology?
X ≡ Y | |
X → Y | |
Y → X | |
¬Y → X |
⇒ ∼(P∨Q) ∨ R
⇒ (∼P∧∼Q) ∨ R
⇒ (∼P∨R) × (∼Q∨R)
⇒ (P→R) ∧ (Q→R)
Option B: X→Y
[(P→R) × (Q→R)] → [(P→R) ∨ (Q→R)]
∼[(P→R) × (Q→R) ∨ (P→R) ∨ (Q→R)]
[∼(P→R) ∨ ∼(Q→R)] ∨ [(P→R) ∨ (Q→R)]
[∼(P→R) ∨ (P→R)] ∨ [∼(P→R) ∨ (Q→R)] ∨ [(Q→R) ∨ (P→R)] ∨ [∼(Q→R) ∨ (Q→R)]
T ∨ [∼(P→R) ∨ (Q→R)] ∨ [(Q→R) ∨ (P→R)] V T
T (✔️)
Question 28 |
What is the first order predicate calculus statement equivalent to the following?
Every teacher is liked by some student
∀(x) [teacher(x) → ∃ (y) [student(y) → likes (y, x)]] | |
∀(x) [teacher(x) → ∃ (y) [student(y) ∧ likes (y, x)]] | |
∃(y) ∀(x) [teacher(x) → [student(y) ∧ likes (y, x)]] | |
∀(x) [teacher(x) ∧ ∃ (y)[student(y) → likes (y, x)]] |
Option B: If x is a teacher, then there exists some y, who is a student and like x. (✔️)
Option C: There exists a student who likes all teachers.
Option D: If x is a teacher and then there exists some y, if y is a student then y likes x.
Question 29 |
∃x P(x) ∧ ∀yQ(x, y) | |
∀x∀yQ(x, y) | |
∃y∀x P(x) ⇒ Q(x, y) | |
∃x P(x) ∧ ∃yQ(x, y) |
Question 30 |
Which one of the following well formed formulae is a tautology?
∀x ∃y R(x,y) ↔ ∃y ∀x R(x,y)
| |
(∀x [∃y R(x,y) → S(x,y)]) → ∀x∃y S(x,y)
| |
[∀x ∃y (P(x,y) → R(x,y)] ↔ [∀x ∃y (¬ P(x,y)∨R(x,y)] | |
∀x ∀y P(x,y) → ∀x ∀y P(y,x) |
[∀x ∃y (P(x,y) → R(x,y)] ↔ [∀x ∃y (¬ P(x,y)∨R(x,y)] is a tautology.
Question 31 |

A | |
B | |
C | |
D |
Question 32 |
(i) false
(ii) Q
(iii) true
(iv) P ∨ Q
(v) ¬Q ∨ P
The number of expressions given above that are logically implied by P ∧ (P ⇒ Q) is _________.
4 | |
5 | |
6 | |
7 |
(P ∧ (P → Q))→ expression is a tautology. So we have to find
How many tautological formulas are there for the given inputs.
(P ∧ (P → Q)) → True is always tautology
(P ∧ (P → Q)) → False is not a tautology
(P ∧ (P → Q)) → Q is a tautology
(P ∧ (P → Q)) → ¬Q ∨ P is a tautology
(P ∧ (P → Q)) → P ∨ Q is a tautology
So there are 4 expressions logically implied by (P ∧ (P → Q))
Question 33 |
Which one of the following well-formed formulae in predicate calculus is NOT valid?
(∀x p(x) ⇒ ∀x q(x)) ⇒ (∃x ¬p(x) ∨ ∀x q(x)) | |
(∃x p(x) ∨ ∃x q(x)) ⇒ ∃x (p(x) ∨ q(x)) | |
∃x (p(x) ∧ q(x)) ⇒ (∃x p(x) ∧ ∃x q(x)) | |
∀x (p(x) ∨ q(x)) ⇒ (∀x p(x) ∨ ∀x q(x)) |
But in option (D), we can generate T → F.
Hence, not valid.
Question 34 |
Consider the first order predicate formula φ:
- ∀x[(∀z z|x ⇒ ((z = x) ∨ (z = 1))) ⇒ ∃w (w > x) ∧ (∀z z|w ⇒ ((w = z) ∨ (z = 1)))]
Here 'a|b' denotes that 'a divides b', where a and b are integers. Consider the following sets:
-
S1. {1, 2, 3, ..., 100}
S2. Set of all positive integers
S3. Set of all integers
Which of the above sets satisfy φ?
S1 and S3 | |
S1, S2 and S3 | |
S2 and S3 | |
S1 and S2 |
One of the case:
If -7 is a number which is prime (either divided by -7 or 1 only). then there exists some number like -3 which is larger than -7 also satisfy the property (either divided by -3 or 1 only).
So, S3 is correct
It's true for all integers too.
Question 35 |
I. p ⇒ q
II. q ⇒ p
III. (¬q) ∨ p
IV. (¬p) ∨ q
I only | |
I and IV only | |
II only | |
II and III only |
Construct Truth tables:
~p ⇒ ~q

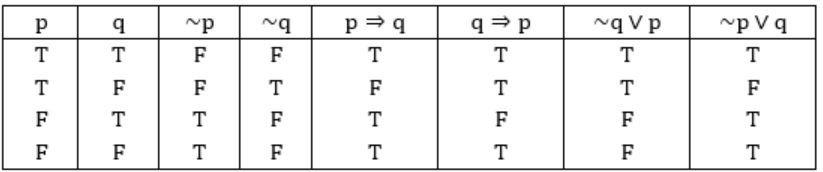
II, III are equivalent to (~p) ⇒ (~q)
Method 2:
(I) p⇒q ≡ ~p∨q
(II) q⇒p ≡ ~q∨p
(III) (~q) ∨ p ≡ ~q∨p
(IV) (~p) ∨ p ≡ ~p∨q
Also, from question:
(~p) ⇒ (~q)
≡ p∨~q
So, (II) & (III) are equivalent to the statement given in question.
Question 36 |
S1: (P # Q) # R = P # (Q # R)
S2: Q # R = R # Q
Which of the following is/are true for the Boolean variables P, Q and R?
Only S1 is True | |
Only S2 is True | |
Both S1 and S2 are True | |
Neither S1 nor S2 are True |
Question 37 |
Suppose the predicate F(x, y, t) is used to represent the statement that person x can fool person y at time t. Which one of the statements below expresses best the meaning of the formula ∀x∃y∃t(¬F(x,y,t))?
Everyone can fool some person at some time | |
No one can fool everyone all the time | |
Everyone cannot fool some person all the time
| |
No one can fool some person at some time |
For better understanding propagate negation sign outward by applying Demorgan's law.
∀x∃y∃t(¬F(x, y, t)) ≡ ¬∃x∀y∀t(F(x,y,t))
Now converting ¬∃x∀y∀t(F(x,y,t)) to English is simple.
¬∃x∀y∀t(F(x,y,t)) ⇒ There does not exist a person who can fool everyone all the time.
Which means "No one can fool everyone all the time".
Hence, Option (B) is correct.
Question 38 |
Let Graph(x) be a predicate which denotes that x is a graph. Let Connected(x) be a predicate which denotes that x is connected. Which of the following first order logic sentences DOES NOT represent the statement: “Not every graph is connected”?
¬∀x (Graph (x) ⇒ Connected (x)) | |
¬∃x (Graph (x) ∧ ¬Connected (x)) | |
¬∀x (¬Graph (x) ∨ Connected (x)) | |
∀x (Graph (x) ⇒ ¬Connected (x))
|
Given expression is
¬∀x(¬Graph(x) ∨ Connected(x)
which can be rewritten as,
¬∀x(Graph(x) ⇒ Connected(x)
which is equivalent to option (A)
(∵ ¬p∨q ≡ p→q)
So, option (A) and (C) cannot be the answer.
Coming to option (B), the given expression is,
∃x (Graph (x) ∧ ¬Connected (x))
"There exist some graph which is not connected", which is equivalent in saying that "Not every graph is connected".
Coming to option (D),
For all x graph is not connected, which is not correct.
Hence, option (D) is the answer.
Question 39 |
Which one of the following is the most appropriate logical formula to represent the statement?
“Gold and silver ornaments are precious”.
The following notations are used:
G(x): x is a gold ornament
S(x): x is a silver ornament
P(x): x is precious∀x(P(x) → (G(x) ∧ S(x))) | |
∀x((G(x) ∧ S(x)) → P(x)) | |
∃x((G(x) ∧ S(x)) → P(x) | |
∀x((G(x) ∨ S(x)) → P(x))
|
(A) for all ornaments, if it is precious then they should be gold and silver.
But, given statement does not says that, “ only gold and silver are precious “ . So this is wrong.
(B) For all ornaments, which contains gold and silver are precious.

Which is only the shaded region in the venn diagrams. But, it misses p,r regions. So, this is wrong option.
C) Some ornaments, which are gold and silver are precious. It is false, because all gold or silver ornaments are precious.
D) For all ornaments, Any ornament which is gold or silver is precious. Which is true.
Question 40 |
The binary operation □ is defined as follows

Which one of the following is equivalent to P ∨ Q ?
¬Q□¬P | |
P□¬Q | |
¬P□Q | |
¬P□¬Q |

P∨Q = P□️Q
So, option B is correct.
