Searching
Question 1 |
Which one of the following statements is false?
Optimal binary search tree construction can be performed efficiently using dynamic programming. | |
Breadth-first search cannot be used to find connected components of a graph. | |
Given the prefix and postfix walks over a binary tree, the binary tree cannot be uniquely constructed. | |
Depth-first search can be used to find connected components of a graph. |
Question 1 Explanation:
In BFS algorithm, we can randomly select a source vertex and then run, after that whether we need to check distance to each and every vertex from source is still infinite (or) not. If we find any vertex having infinite distance then the graph is not connected.
Question 2 |
Consider the following algorithm for searching for a given number x in an unsorted array A[1...n] having n distinct values:
1. Choose an i uniformly at random from 1...n;
2. If A[i]=x then Stop else Goto 1;
Assuming that x is present in A, what is the expected number of comparisons made by the algorithm before it terminates?
n | |
n-1 | |
2n | |
n/2 |
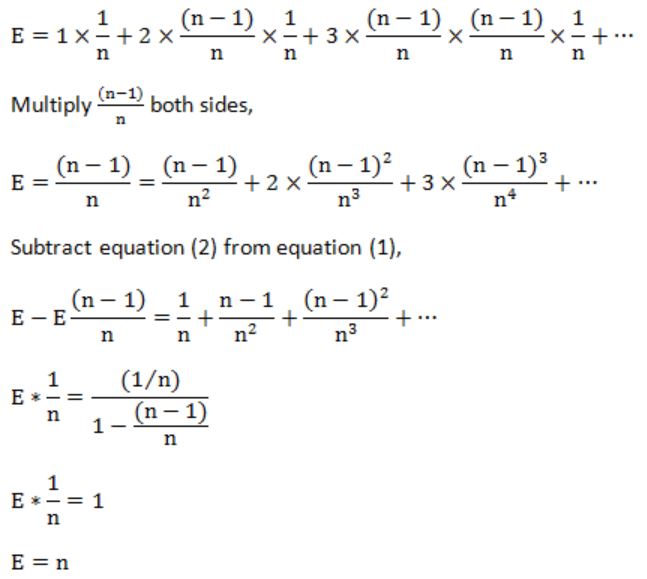
Question 2 Explanation:
Question 3 |
Consider the C function given below. Assume that the array listA contains n (> 0) elements, sorted in ascending order.
int ProcessArray(int *listA, int x, int n)
{
int i, j, k;
i = 0;
j = n-1;
do
{
k = (i+j)/2;
if (x <= listA[k])
j = k-1;
if (listA[k] <= x)
i = k+1;
}
while (i <= j);
if (listA[k] == x)
return(k);
else
return -1;
}
Which one of the following statements about the function ProcessArray is CORRECT?
It will run into an infinite loop when x is not in listA. | |
It is an implementation of binary search. | |
It will always find the maximum element in listA. | |
It will return −1 even when x is present in listA. |
Question 3 Explanation:
From the above code, we can identify
k = (i+j)/2;
where k keeps track of current middle element & i, j keeps track of left & right children of current subarray.
So it is an implementation of Binary search.
k = (i+j)/2;
where k keeps track of current middle element & i, j keeps track of left & right children of current subarray.
So it is an implementation of Binary search.
Question 4 |
Let A be an array of 31 numbers consisting of a sequence of 0’s followed by a sequence of 1’s. The problem is to find the smallest index i such that A[i] is 1 by probing the minimum number of locations in A. The worst case number of probes performed by an optimal algorithm is _________.
5 | |
6 | |
7 | |
8 |
Question 4 Explanation:
→ If we apply binary search to find the first occurrence of 1 in the list, it will give us the smallest index i where 1 is stored.
→ As in this array sequence of 0’s is followed by sequence of 1’s, the array is sorted. We can apply binary search directly without sorting it.
So number of probes = ceil(log2 31) = 4.954196310386876
⇒ here we are using ceiling so it becomes 5
→ As in this array sequence of 0’s is followed by sequence of 1’s, the array is sorted. We can apply binary search directly without sorting it.
So number of probes = ceil(log2 31) = 4.954196310386876
⇒ here we are using ceiling so it becomes 5
Question 5 |
Which of the following is the recurrence relation for binary search?
T(n) = T(n/2) + 1 | |
T(n) = T(n/2) + n | |
T(n) = 2T(n - 1) + 1 | |
T(n) = T(n - 1) + 1 |
Question 5 Explanation:
A-applying masters theorem we get O(logn) which is the time complexity of binary search.
B- applying masters theorem we get O(n) which is not the time complexity for binary search.
C- Using back substitution we get O(2n) which is not the time complexity for binary search.
D-Using back substitution we get time complexity as O(n) which is not of binary search.
B- applying masters theorem we get O(n) which is not the time complexity for binary search.
C- Using back substitution we get O(2n) which is not the time complexity for binary search.
D-Using back substitution we get time complexity as O(n) which is not of binary search.
Question 6 |
What is the best case running time of binary search?
θ(n) | |
θ(1) | |
θ(log n) | |
θ(n log log n) |
Question 6 Explanation:
Best case running time complexity of binary search is O(1) and worst case running time complexity of binary search is O(log n).
Question 7 |
If the binary search algorithm determines that the search argument is in the lower half of the array, which of the following statements will set the appropriate variable to the appropriate value?
Start Sub = Middle Sub – 1 : | |
Start Sub = Middle Sub + 1 : | |
Stop Sub = Middle Sub – 1 : | |
Stop Sub = Middle Sub + 1 : |
Question 7 Explanation:
if search argument is in lower half then, no need to search in upper half and middle one is already checked so, Stop Sub = Middle Sub – 1 :
There are 7 questions to complete.