Set-Theory
Question 1 |
59049 |

Question 2 |
The number of elements in he power set P (S) of the set S = {(φ), 1, (2, 3)} is:
2 | |
4 | |
8 | |
None of the above |
P(S) = {φ, {{φ}}, {1}, {{2, 3}}, {{φ}, 1}, {1, {2, 3}}, {{φ}, 1, {2, 3}}}
In P(S) it contains 8 elements.
Question 3 |
Let G be a group of 35 elements. Then the largest possible size of a subgroup of G other than G itself is ______.
7 |
If ‘H” is a subgroup of finite group (G,*) then O(H) is the divisor of O(G).
Given that the order of group is 35. Its divisors are 1,5,7,35.
It is asked that the size of largest possible subgroup other than G itself will be 7.
Question 4 |
Let G be a finite group on 84 elements. The size of a largest possible proper subgroup of G is _________.
41 | |
42 | |
43 | |
44 |
For any group ‘G’ with order ‘n’, every subgroup ‘H’ has order ‘k’ such that ‘n’ is divisible by ‘k’.
Solution:
Given order n = 84
Then the order of subgroups = {1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84}
As per the proper subgroup definition, it should be “42”.
Question 5 |
Suppose A = {a,b,c,d} and Π1 is the following partition of A
Π1 = {{a,b,c}{d}}
(a) List the ordered pairs of the equivalence relations induced by Π1.
(b) Draw the graph of the above equivalence relation.
(c) Let Π2 = {{a},{b},{C},{d}}
Π3 = {{a,b,c,d}}
and Π4 = {{a,b},{c,d}}
Draw a Poset diagram of the poset,
({Π1,Π2,Π3,Π4}, refines⟩
Theory Explanation. |
Question 6 |
The number of subsets {1, 2, ... n} with odd cardinality is __________.
2n-1 |
And so, no. of subsets with odd cardinality is half of total no. of subsets = 2n /n = 2n-1
Question 7 |
Let S be an infinite set and S1 ..., Sn be sets such that S1 ∪ S2 ∪ ... ∪ Sn = S. Then,
at least one of the set Si is a finite set | |
not more than one of the set Si can be finite | |
at least one of the sets Si is an infinite set | |
not more than one of the sets Si can be infinite | |
None of the above |
Question 8 |
Let A be a finite set of size n. The number of elements in the power set of A × A is:
22n | |
2n2 | |
(2n)2 | |
(22)n | |
None of the above |
A = {1,2}
|A| = {∅, {1}, {2}, {1,2}}
Cardinality of power set of A = 2n2
A × A = {1,2} × {1,2}
= {(1,1), (1,2), (2,1), (2,2)}
Cardinality of A × A = n2
Cardinality of power set of A × A = 2n2
Question 9 |
If a relation S is reflexive and circular, then S is an equivalence relation. | |
If a relation S is transitive and circular, then S is an equivalence relation. | |
If a relation S is circular and symmetric, then S is an equivalence relation. | |
If a relation S is reflexive and symmetric, then S is an equivalence relation. |
Theorem: A relation R on a set A is an equivalence relation if and only if it is reflexive and circular.
For symmetry, assume that x, y ∈ A so that xRy, lets check for yRx.
Since R is reflexive and y ∈ A, we know that yRy. Since R is circular and xRy and yRy, we know that yRx. Thus R is symmetric.
For transitivity, assume that x, y, z ∈ A so that xRy and yRz. Check for xRz. Since R is circular and xRy and yRz, we know that zRx. Since we already proved that R is symmetric, zRx implies that xRz. Thus R is transitive.
Question 10 |
Let f be a function from a set A to a set B, g a function from B to C, and h a function from A to C, such that h(a) = g(f(a)) for all a ∈ A. Which of the following statements is always true for all such functions f and g?
g is onto ⇒ h is onto | |
h is onto ⇒ f is onto | |
h is onto ⇒ g is onto | |
h is onto ⇒ f and g are onto |
If h: A→C is a onto function, the composition must be onto, but the first function in the composition need to be onto.
So, B→C is must be onto.
Question 11 |
Let A be a set with n elements. Let C be a collection of distinct subsets of A such that for any two subsets S1 and S2 in C, either S1 ⊂ S2 or S2 ⊂ S1. What is the maximum cardinality of C?
n | |
n + 1 | |
2(n-1) + 1 | |
n! |
Let A = {a, b, c}, here n = 3
Now, P(A) = {Ø, {a}, {b}, {c}, {a,b}, {b,c}, {{a}, {a,b,c}}
Now C will be contain Ø (empty set) and {a,b,c} (set itself) as Ø is the subset of every set. And every other subset is the subset of {a,b,c}.
Now taking the subset of cardinality, we an take any 1 of {a}, {b}, {c} as none of the set is subset of other.
Let's take {2}
→ Now taking the sets of cardinality 2 -{a,b}, {b,c}
→ {b} ⊂ {a,b} and {b,c} but we can't take both as none of the 2 is subset of the other.
→ So let's take {c,a}.
So, C = {Ø, {b}, {b,c}, {a,b,c}}
→ So, if we observe carefully, we can see that we can select only 1 set from the subsets of each cardinality 1 to n
i.e., total n subsets + Ø = n + 1 subsets of A can be there in C.
→ So, even though we can have different combinations of subsets in C but maximum cardinality of C will be n+1 only.
Question 12 |
Let n = p2q, where p and q are distinct prime numbers. How many numbers m satisfy 1 ≤ m ≤ n and gcd (m, n) = 1? Note that gcd (m, n) is the greatest common divisor of m and n.
p(p - 1) | |
pq | |
(p2 - 1)(q - 1) | |
p(p - 1)(q - 1) |
→ No. of multiples of p in n = pq [n = p⋅p⋅q]
→ No. of multiples of q in n = p2 [n = p2q]
→ Prime factorization of n contains only p & q.
→ gcd(m,n) is to be multiple of p and (or) 1.
→ So, no. of possible m such that gcd(m,n) is 1 will be
n - number of multiples of either p (or) q
= n - p2 - pq + p
= p2q - p2 - pq + p
= p(pq - p - q + 1)
= p(p - 1)(q - 1)
Question 13 |
If the longest chain in a partial order is of length n then the partial order can be written as a ______ of n antichains.
disjoint |
Question 14 |
Consider the set X = {a,b,c,d e} under the partial ordering
- R = {(a,a),(a,b),(a,c),(a,d),(a,e),(b,b),(b,c),(b,e),(c,c),(c,e),(d,d),(d,e),(e,e)}.
The Hasse diagram of the partial order (X,R) is shown below.
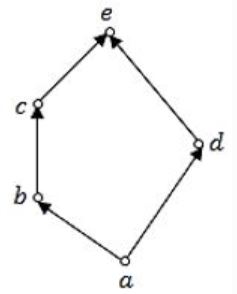
The minimum number of ordered pairs that need to be added to R to make (X,R) a lattice is _________.
0 | |
1 | |
2 | |
3 |
As per the definition of lattice, each pair should have GLB, LUB.
The given ‘R’ has GLB, LUB for each and every pair.
So, no need to add extra pair.
Thus no. of required pair such that Hasse diagram to become lattice is “0”.
Question 15 |
AΔB = (A − B) ∪ (B − A) .
Let H = (2x, Δ). Which of the following statements about H is/are correct?
H is a group. | |
Every element in H has an inverse, but H is NOT a group. | |
For every A ε 2x, the inverse of A is the complement of A. | |
For every A ε 2x, the inverse of A is A. |
Question 16 |
Let R be the relation on the set of positive integers such that aRb if and only if a and b are distinct and have a common divisor other than 1. Which one of the following statements about R is true?
R is symmetric and reflexive but not transitive | |
R is reflexive but not symmetric and not transitive | |
R is transitive but not reflexive and not symmetric | |
R is symmetric but not reflexive and not transitive |
In aRb, 'a' and 'b' are distinct. So it can never be reflexive.
Symmetric:
In aRb, if 'a' and 'b' have common divisor other than 1, then bRa, i.e., 'b' and 'a' also will have common divisor other than 1. So, yes symmetric.
Transitive:
Take (3, 6) and (6, 2) elements of R. For transitivity (3, 2) must be the element of R, but 3 and 2 don't have a common divisor. So not transitive.
Question 17 |
The cardinality of the power set of {0, 1, 2, … 10} is _________.
2046 | |
2047 | |
2048 | |
2049 |
Question 18 |
Suppose L = {p, q, r, s, t} is a lattice represented by the following Hasse diagram:

For any x, y ∈ L, not necessarily distinct, x ∨ y and x ∧ y are join and meet of x, y respectively. Let L3 = {(x,y,z): x, y, z ∈ L} be the set of all ordered triplets of the elements of L. Let pr be the probability that an element (x,y,z) ∈ L3 chosen equiprobably satisfies x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z). Then
pr = 0 | |
pr = 1 | |
0 < pr ≤ 1/5 | |
1/5 < pr < 1 |
Let A be the event that an element (x,y,z)∈ L3 satisfies x ∨(y∧z) = (x∨y) ∧ (x∨z) Since q∨(r∧s) = q∨p = q
and (q∨r)∧(q∨s) = t∧t = t q∨(r∧s) ≠ (q∨r)∧(q∨s)
Therefore, (x,y,z) = (q,r,s),(q,s,r),(r,q,s),(r,s,q),(s,r,q),(s,q,r)
i.e., 3! = 6 elements will not satisfy distributive law and all other (x,y,z) choices satisfy distributive law
n(A) = 125-6 = 119
∴ required probability is 119/125
⇒ 1/5
Question 19 |
Consider the operations f(X, Y, Z) = X'YZ + XY' + Y'Z' and g(X′, Y, Z) = X′YZ + X′YZ′ + XY Which one of the following is correct?
Both {f} and {g} are functionally complete | |
Only {f} is functionally complete | |
Only {g} is functionally complete
| |
Neither {f} nor {g} is functionally complete |
f(X,X,X) = X'XX'+XX'+X'X'
= 0+0+X'
= X'
Similarly, f(Y,Y,Y) = Y' and f(X,Z,Z) = Z'
f(Y',Y',Z') = (Y')'Y'Z'+Y'(Y')'+(Y')'(Z')'
= YY'Z'+Y'Y+YZ
= 0+0+YZ
= YZ
We have derived NOT and AND. So f(X,Y,Z) is functionally complete.
g(X,Y,Z) = X'YZ+X'YZ'+XY
g(X,X,X) = X'XX+X'XZ'+XX
= 0+0+X
= X
Similarly, g(Y,Y,Y) = Y and g(Z,Z,Z) = Z
NOT is not derived. Hence, g is not functionally complete.
Question 20 |
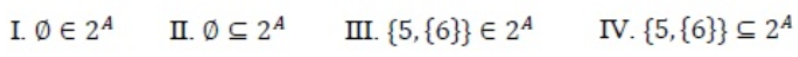
I and III only | |
II and III only | |
I, II and III only | |
I, II and IV only |
Question 21 |
P:R is reflexive
Q:R is transitive
Which one of the following statements is TRUE?
Both P and Q are true. | |
P is true and Q is false. | |
P is false and Q is true. | |
Both P and Q are false. |
a≤c ∨ b≤d
Let a≤a ∨ b≤b is true for all a,b ∈ N
So there exists (a,a) ∀ a∈N.
It is Reflexive relation.
Consider an example
c = (a,b)R(c,d) and (c,d)R(e,f) then (a,b)R(e,f)
This does not hold for any (a>e) or (b>f)
eg:
(2,2)R(1,2) as 2≤2
(1,2)R(1,1) as 1≤1
but (2,2) R (1,1) is False
So, Not transitive.
Question 22 |
I. Each compound in U\S reacts with an odd number of compounds.
U\S reacts with an odd number of compounds.
U\S reacts with an even number of compounds.
ALWAYS TRUE?
Only I | |
Only II | |
Only III | |
None |
U = 23
∃S ∋ (S⊂U)
Each component in ‘S’ reacts with exactly ‘3’ compounds of U,
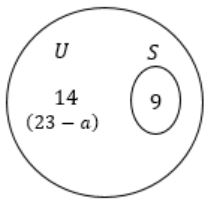
If a component ‘a’ reacts with ‘b’, then it is obvious that ‘b’ also reacts with ‘a’.
It’s a kind of symmetric relation.>br> If we connect the react able compounds, it will be an undirected graph.
The sum of degree of vertices = 9 × 3 = 27
But, in the graph of ‘23’ vertices the sum of degree of vertices should be even because
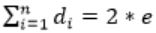 (di = degree of vertex i.e., = no. of edges)
(di = degree of vertex i.e., = no. of edges)But ‘27’ is not an even number.
To make it an even, one odd number should be added.
So, there exists atleast one compound in U/S reacts with an odd number of compounds.
Question 23 |
R: ∀a,b ∈ G, aRb if and only if ∃g ∈ G such that a = gbg
R: ∀a,b ∈ G, aRb if and only if a = b-1
Which of the above is/are equivalence relation/relations?
R2 only | |
R1 and R2 | |
Neither R1 and R2 | |
R1 only |
Consider Statement R1:
Reflexive:
aR1a
⇒ a = g-1ag
Left multiply both sides by g
⇒ ga = gg-1ag
Right multiply both sides by g-1
⇒ gag-1 = gg-1agg-1
⇒ gag-1 = a [∴ The relation is reflexive]
Symmetric:
If aR1b, then ∃g ∈ G such that gag-1 = b then a = g-1bg, which is Correct.
⇒ So, given relation is symmetric.
Transitive:
The given relation is Transitive.
So, the given relation R1 is equivalence.
R2:
The given relation is not reflexive.
So, which is not equivalence relation.
Such that a ≠ a-1.
So, only R1 is true.
Question 24 |

Which of the above statements is/are TRUE?
Only II | |
Only I | |
Neither I nor II | |
Both I and II |
and given A = {(x, X), x∈X and X⊆U}
Possible sets for U = {Φ, {1}, {2}, {1, 2}}
if x=1 then no. of possible sets = 2
x=2 then no. of possible sets = 2
⇒ No. of possible sets for A = (no. of sets at x=1) + (no. of sets at x=2) = 2 + 2 = 4
Consider statement (i) & (ii) and put n=2
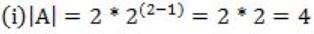
Statement (i) is true
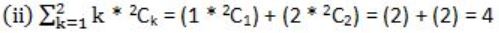
Statement (i) and (ii) both are true.
Answer: (C)
Video Explanation
Question 25 |
f(n) = f(n/2) if n is even
f(n) = f(n+5) if n is odd
Let R = {i|∃j: f(j)=i} be the set of distinct values that f takes. The maximum possible size of R is __________.
2 | |
3 | |
4 | |
5 |
f(n)= f(n+5) if n is odd

We can observe that
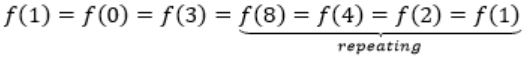
and f(5) = f(10) = f(15) = f(20)
Observe that f(11) = f(8)
f(12) = f(6) = f(3)
f(13) = f(9) = f(14) = f(7) = f(12) = f(6) = f(3)
f(14) = f(9) = f(12) = f(6) = f(3)
f(16) = f(8) = f(4) = f(2) = f(1) [repeating]
So, we can conclude that
‘R’ can have size only ‘two’ [one: multiple of 5’s, other: other than 5 multiples]
Question 26 |
Suppose U is the power set of the set S = {1, 2, 3, 4, 5, 6}. For any T ∈ U, let |T| denote the number of element in T and T' denote the complement of T. For any T, R ∈ U, let TR be the set of all elements in T which are not in R. Which one of the following is true?
∀X ∈ U (|X| = |X'|) | |
∃X ∈ U ∃Y ∈ U (|X| = 5, |Y| = 5 and X ∩ Y = ∅) | |
∀X ∈ U ∀Y ∈ U (|X| = 2, |Y| = 3 and X \ Y = ∅) | |
∀X ∈ U ∀Y ∈ U (X \ Y = Y' \ X') |
(A) False. Consider X = {1,2}. Therefore, X' = {3,4,5,6}, |X| = 2 and |X'| = 4.
(B) False. Because for any two possible subsets of S with 5 elements should have atleast 4 elements in common. Hence X∩Y cannot be null.
(C) False. Consider X = {1,4}, Y= {1,2,3} then X\Y = {4} which is not null.
(D) True. Take any possible cases.
Question 27 |
Let R be a relation on the set of ordered pairs of positive integers such that ((p,q),(r,s)) ∈ R if and only if p - s = q - r. Which one of the following is true about R?
Both reflexive and symmetric | |
Reflexive but not symmetric | |
Not reflexive but symmetric | |
Neither reflexive nor symmetric |
∴(p,q) R (p,q)
⇒ R is not reflexive.
Let (p,q) R (r,s) then p-s = q-r
⇒ r-q = s-p
⇒ (r,s) R (p,q)
⇒ R is symmetric.
Question 28 |
A binary operation ⊕ on a set of integers is defined as x ⊕ y = x2 + y2. Which one of the following statements is TRUE about ⊕?
Commutative but not associative | |
Both commutative and associative | |
Associative but not commutative | |
Neither commutative nor associative |
A binary relation on a set S is called cumulative if a*b = b*a ∀ x,y∈S.
Associative property:
A binary relation on set is called associative if (a*b)*c = a*(b*c) ∀ x,y∈S.
Given x⊕y = x2 + y2 --------(1)
Replace x, y in (1)
y⊕x = y2 + x2 which is same as (1), so this is cumulative
(x⊕y)⊕z = (x2 + y2) ⊕ z
= (x2 + y2) + z2
= x2 + y2 + z2 + 2x2y2 ----------(2)
x⊕(y ⊕ z) = x ⊕ (y2 + z2)
= x2 + (y2 + z2)2
= x2 + y2 + z2 + 2y2z2 ----------- (3)
(2) & (3) are not same so this is not associative.
Question 29 |
Let X and Y be finite sets and f: X→Y be a function. Which one of the following statements is TRUE?
For any subsets A and B of X, |f(A ∪ B)| = |f(A)|+|f(B)| | |
For any subsets A and B of X, f(A ∩ B) = f(A) ∩ f(B) | |
For any subsets A and B of X, |f(A ∩ B)| = min{ |f(A)|,f|(B)|} | |
For any subsets S and T of Y, f -1 (S ∩ T) = f -1 (S) ∩ f -1 (T) |
We need to consider subsets of 'x', which are A & B (A, B can have common elements are exclusive).
Similarly S, T are subsets of 'y'.

To be a function, each element should be mapped with only one element.
(a) |f(A∪B)| = |f(A)|+|f(B)|
|{a,b,c}|∪|{c,d,e}| = |{a,b,c}| + |{c,d,e}|
|{a,b,c,d,e}| = 3+3
5 = 6 FALSE
(d) To get inverse, the function should be one-one & onto.
The above diagram fulfills it. So we can proceed with inverse.
f-1 (S∩T ) = f-1 (S)∩f-1 (T)
f-1 (c) = f-1 ({a,b,c})∩f-1 ({c,d,e})
2 = {1,2,3}∩{2,4,5}
2 = 2 TRUE
Question 30 |
Let G be a group with 15 elements. Let L be a subgroup of G. It is known that L ≠ G and that the size of L is at least 4. The size of L is __________.
5 | |
6 | |
7 | |
8 |
So, 15 is divided by {1, 3, 5, 15}.
As minimum is 4 and total is 15, we eliminate 1,3,15.
Answer is 5.
Question 31 |
If V1 and V2 are 4-dimensional subspace of a 6-dimensional vector space V, then the smallest possible dimension of V1∩V2 is ______.
2 | |
3 | |
4 | |
5 |
For eg: a two dimensional vector space have x, y axis. For dimensional vector space, it have x, y, z axis.
In the same manner, 6 dimensional vector space has x, y, z, p, q, r (assume).
Any subspace of it, with 4 dimensional subspace consists any 4 of the above. Then their intersection will be atmost 2.
[{x,y,z,p} ∩ {r,q,p,z}] = #2
V1 ∩ V2 = V1 + V2 - V1 ∪ V2 = 4 + 4 + (-6) = 2
