Sets-And Relation
Question 1 |
Let R be the set of all binary relations on the set {1,2,3}. Suppose a relation is chosen from R at random. The probability that the chosen relation is reflexive (round off to 3 decimal places) is _____.
0.125 |
The number of reflexive relations is 2^(n^2-n).
The total number of relations on a set with n elements is 2^ (n^2).
The probability of choosing the reflexive relation out of set of relations is
= 2^(n^2-n) /2^ (n^2)
= 2^( n^2-n- n^2)
= 2^(-n)
Given n=3, the probability will be 2-n = ⅛ = 0.125
Question 2 |
Let (S, ≤) be a partial order with two minimal elements a and b, and a maximum element c. Let P: S → {True, False} be a predicate defined on S. Suppose that P(a) = True, P(b) = False and P(x) ⇒ P(y) for all x, y ∈ S satisfying x ≤ y, where ⇒ stands for logical implication. Which of the following statements CANNOT be true?
P(x) = True for all x ∈ S such that x ≠ b
| |
P(x) = False for all x ∈ S such that x ≠ a and x ≠ c | |
P(x) = False for all x ∈ S such that b ≤ x and x ≠ c | |
P(x) = False for all x ∈ S such that a ≤ x and b ≤ x |
a or b the minimal element in set.
P(a) = True for all x ∈ S such that a ≤ x and b ≤ x.
Option D is False.
Question 3 |
Consider the set S = {a,b,c,d}. Consider the following 4 partitions π1, π2, π3, π4 on ![]() Let p be the partial order on the set of partitions S' = {π1, π2, π3, π4} defined as follows: πi p πj if and only if πi refines πj. The poset diagram for (S', p) is:
Let p be the partial order on the set of partitions S' = {π1, π2, π3, π4} defined as follows: πi p πj if and only if πi refines πj. The poset diagram for (S', p) is:
 | |
 | |
 | |
 |
And, neither π2 refines π3, nor π3 refines π2.
Here, only π1 refined by every set, so it has to be at the top.
Finally, option C satisfies all the property.
Question 4 |
What is the possible number of reflexive relations on a set of 5 elements?
210 | |
215 | |
220 | |
225 |
Definition of Reflexive relation:
A relation ‘R’ is reflexive if it contains xRx ∀ x∈A
A relation with all diagonal elements, it can contain any combination of non-diagonal elements.
Eg:
A={1, 2, 3}

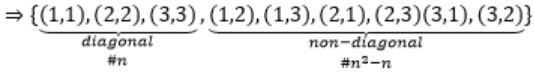
So for a relation to be reflexive, it should contain all diagonal elements. In addition to them, we can have possible combination of (n2-n)non-diagonal elements (i.e., 2n2-n)
Ex:
{(1,1)(2,2)(3,3)} ----- ‘0’ non-diagonal element
{(1,1)(2,2)(3,3)(1,2)} ----- ‘1’ non-diagonal element
{(1,1)(2,2)(3,3)(1,2)(1,3)} “
___________ “
___________ “
{(1,1)(2,2)(3,3)(1,2)(1,3)(2,1)(2,3)(3,1)(3,2)} (n2-n) diagonal elements
____________________
Total: 2n2-n
For the given question n = 5.
The number of reflexive relations = 2(25-5) = 220
Question 5 |
Consider the set S = {1, ω, ω2}, where ω and ω2 are cube roots of unity. If * denotes the multiplication operation, the structure (S,*) forms
A group | |
A ring | |
An integral domain | |
A field |
1) Closure
2) Associativity
3) Have Identity element
4) Invertible
Over ‘*’ operation the S = {1, ω, ω2} satisfies the above properties.
The identity element is ‘1’ and inverse of 1 is 1, inverse of ‘w’ is 'w2' and inverse of 'w2' is 'w'.
Question 6 |
Which one of the following in NOT necessarily a property of a Group?
Commutativity
| |
Associativity | |
Existence of inverse for every element
| |
Existence of identity |
So, commutativity is not required.
