Time-Complexity
Question 1 |
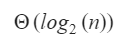 | |
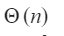 | |
 | |
 |
In this question they given three main constraints
- The input array is in sorted order
- Use recursive binary search
- Worst case number of operations
If the array is in sorted order then the worst case time complexity is O(logn)
Ex: 10, 20, 30
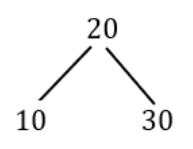
The binary search approach is using either recursive or iterative method is
Step-1: element = middle, the element is found and return the index.
Step-2: element > middle, search for the element in the sub-array starting from middle+1 index to n.
Step-3: element < middle, search for element in the sub-array starting from 0 index to middle -1.
Note: The worst case happens when we want to find the smallest/largest farthest node. So, it will not take more than O(logn) time.
Question 2 |
 | |
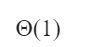 | |
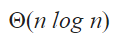 | |
 |
The heap is nothing but a complete binary tree and uses linear search to find the elements.
In min heap, the parent key is less than or equal to (≤) the child keys. The maximum values should present in the farthest leaf node for the worst case time complexity.
To traverse all the elements in a heap will take O(n) time for the worst case because it uses the linear search to find the element.
Question 3 |
Which of the following is false?
 | |
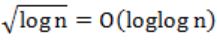 | |
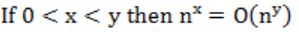 | |
 |

Question 4 |
The recurrence relation
T(1) = 2 T(n) = 3T(n/4)+n
has the solution, T(n) equals to
O(n) | |
O(log n) | |
O(n3/4) | |
None of the above |
Question 5 |
The average number of key comparisons done on a successful sequential search in list of length n is
log n | |
n-1/2 | |
n/2 | |
n+1/2 |
= No. of comparisons if element present in 1st position + No. of comparisons if element present in 2nd position + ............. + No. of comparisons if element present in nth position
= 1 + 2 + 3 + ... + n
= n(n+1)/2
Since there are n elements in the list, so average no. of comparisons
= Total comparisons/Total no. of elements
= (n(n+1)/2)/n
= n+1/2
Question 6 |
Quicksort is run on two inputs shown below to sort in ascending order taking first element as pivot,
(i) 1,2,3,...,n (ii) n,n-1,n-2,...,2,1
Let C1 and C2 be the number of comparisons made for the inputs (i) and (ii) respectively. Then,
C1 < C2 | |
C1 > C2 | |
C1 = C2 | |
we cannot say anything for arbitrary n. |
So, option is (C) is correct.
Question 7 |
Suppose we want to arrange the n numbers stored in any array such that all negative values occur before all positive ones. Minimum number of exchanges required in the worst case is
n - 1 | |
n | |
n + 1 | |
None of the above |
Now we will swap 1st no. with nth no. and then 2nd no. with (n-1)th no. and then 3rd no. with (n-2)th and so on. Like this we will have to do n/2 swaps in worst case.
Question 8 |
If n is a power of 2, then the minimum number of multiplications needed to compute a* is
log2 n | |
√n | |
n-1 | |
n |
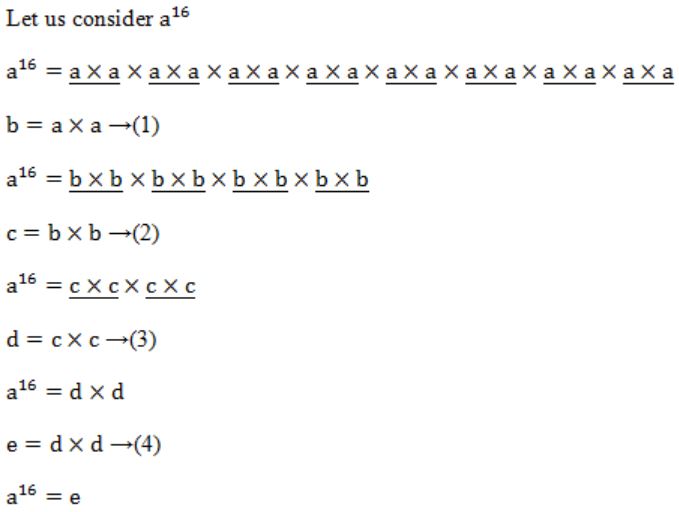
We require 4 multiplications to calculate a16 .....(I)
→ Like that 3 multiplications requires to calculate a8 .....(II)
I, II are satisfied with the option A.
Question 9 |
If T1 = O(1), give the correct matching for the following pairs:
(M) Tn = Tn−1 + n (U) Tn = O(n) (N) Tn = Tn/2 + n (V) Tn = O(nlogn) (O) Tn = Tn/2 + nlogn (W) T = O(n2) (P) Tn = Tn−1 + logn (X) Tn = O(log2n)
M – W N – V O – U P - X | |
M – W N – U O – X P - V | |
M – V N – W O – X P - U | |
None of the above |
(N) Apply Master's theorem
T(n) = θ(n) = O(n)
(O) Apply Master's theorem
T(n) = θ(n logn) = O(n logn)
(P) Here we are adding the log of firstn natural numbers.
So,
Tn = log1 + log2 + log3 + ... + logn
= log (1×2×...n)
= log(n!)
= θ(n logn)
Question 10 |
(a) Consider the following algorithm. Assume procedure A and procedure B take O(1) and O(1/n) unit of time respectively. Derive the time complexity of the algorithm in O-notation.
algorithm what (n)
begin
if n = 1 then call A
else begin
what (n-1);
call B(n)
end
end.
(b) Write a constant time algorithm to insert a node with data D just before the node with address p of a singly linked list.
Theory Explanation. |
Question 11 |
Consider the following functions

Which of the following is true?
h(n) is O (f(n)) | |
h(n) is O (g(n)) | |
g(n) is not O (f(n)) | |
f(n) is O(g(n)) |
Then
f(n) = 3(n32) = 3*(210)32 = 3*2320
g(n) = 2320
h(n) = 1024!
So relation between the functions can be:
f(n) and g(n) are of same order, so f(n) is O(g(n)) and g(n) = O(f(n)). Option C is wrong.
h(n) is n! Which is of higher order than f(n) and g(n). So options A and B are wrong.
Question 12 |
Let f(n) = n2logn and g(n) = n(logn)10 be two positive functions of n. Which of the following statements is correct?
f(n) = O(g(n) and g(n) ≠ O(f(n)) | |
g(n) = O(f(n) and f(n) ≠ O(g(n)) | |
f(n) ≠ O(g(n)) and g(n) ≠ O(f(n)) | |
f(n) = O(g(n)) and g(n) = O(f(n)) |
Cancel nlogn from f(n), g(n)
f(n) = n; g(n) = (logn)9
n is too large than (logn)9
So f(n)! = O(g(n)) and g(n) = O(f(n))
Question 13 |
The running time of the following algorithm
Procedure A(n) If n <= 2 return(1) else return (A(⌈√n⌉));
is best described by:
O(n) | |
O(log n) | |
O(log log n) | |
O(1) |
Let n=2m
So, T(2m) = T(2m/2)+1
We substitute T(2m) = S(m),
So now the equation becomes,
S(m) = S(m/2)+1
Now after applying master's theorem,
S(m) = O(log m)
T(n) = O(log log n)
Question 14 |
Consider the following three claims
I. (n + k)m = Θ(nm), where k and m are constants II. 2n+1 = O(2n) III. 22n+1 = O(2n)
Which of these claims are correct?
I and II
| |
I and III | |
II and III | |
I, II, and III |
Which is true by considering leading ordered term present in polynomial expression.
II) 2n+1 = Θ(nm) → True
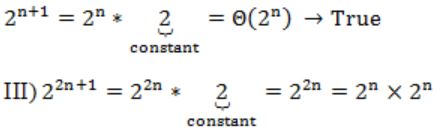
2n×2n can't be written as Θ(2n)
So, this is False.
Question 15 |
The usual Θ(n2) implementation of Insertion Sort to sort an array uses linear search to identify the position where an element is to be inserted into the already sorted part of the array. If, instead, we use binary search to identify the position, the worst case running time will
remain Θ(n2) | |
become Θ(n (log n)2) | |
become Θ(n log n) | |
become Θ(n) |
Instead, linear search use binary search then (log n) will be the worst case time complexity of binary search and performing n swaps to place an element in right position for the corresponding n elements
i.e., n×(logn+n)
Θ((n×logn)+n2)
Θ(n2)
Remains same.
Question 16 |
The cube root of a natural number n is defined as the largest natural number m such that m3≤n. The complexity of computing the cube root of n (n is represented in binary notation) is:
O(n) but not O(n0.5) | |
O(n0.5 but not O((log n)k) for any constant k>0
| |
O((log n)k) for some constant k>0, but not O((log log n)m) for any constant m>0 | |
O((log log n)k) for some constant k>0.5, but not O((log log n)0.5) |
The time complexity is never less than O(log n) because to represent a binary search will takes O(log n) ... (II)
From (I), option A and B False
From (II), option D False.
Question 17 |
The tightest lower bound on the number of comparisons, in the worst case, for comparison-based sorting is of the order of
n | |
n2 | |
nlogn | |
nlog2n |
→ Tightest upper bound is (big O).
Tightest lower bound is (big Ω).
Question 18 |
Two matrices M1 and M2 are to be stored in arrays A and B respectively. Each array can be stored either in row-major or column-major order in contiguous memory locations. The time complexity of an algorithm to compute M1 × M2 will be
best if A is in row-major, and B is in column major order | |
best if both are in row-major order | |
best if both are in column-major order | |
independent of the storage scheme |
But if the question would have asked best time complexity in which of the following implementation (not algorithm) then Option (A) is correct.
Question 19 |
Let A[1,...,n] be an array storing a bit (1 or 0) at each location, and f(m) is a function whose time complexity is θ(m). Consider the following program fragment written in a C like language:
counter = 0;
for (i = 1; i < = n; i++)
{ if (A[i] == 1) counter++;
else { f(counter); counter = 0; }
}
The complexity of this program fragment is
Ω(n2)
| |
Ω(nlogn) and O(n2) | |
θ(n) | |
o(n) |
If the string contains all one's then it takes O(n) time, because counter++ can execute n times.
If it contains half 0's and half 1's then also it takes O(n) time.
Question 20 |
The time complexity of the following C function is (assume n > 0)
int recursive (int n) {
if (n == 1)
return (1);
else
return (recursive (n - 1) + recursive (n - 1));
} O(n) | |
O(n log n) | |
O(n2) | |
O(2n)
|
return(1)
else
return(recursive(n-1) + recursive(n-1))
n>0:
T(2) = T(1) + T(1) = 2T(1)
T(3) = T(2) + T(2) = 2T(2) = 2⋅2T(1) = 22T(1)
T(4) = 23⋅T(1)
⋮
T(n) = 2n⋅T(1) = O(2n)
Question 21 |
A program takes as input a balanced binary search tree with n leaf nodes and computes the value of a function g(x) for each node x. If the cost of computing g(x) is min{no. of leaf-nodes in left-subtree of x, no. of leaf-nodes in right-subtree of x} then the worst-case time complexity of the program is
Θ (n) | |
Θ (n log n) | |
Θ (n2) | |
Θ (n2 log n) |
⇒ g(x) = min (no. of leaf nodes of left-subtree of x, no. of leaf nodes in the right-subtree of x)
→ Total no. of leaves = n
Time complexity for a binary search = log n
Time complexity of the program is = O(n(log n))
Question 22 |
The recurrence relation that arises in relation with the complexity of binary search is:
T(n) = T(n/2) + k, k a constant | |
T(n) = 2T(n/2) + k, k a constant | |
T(n) = T(n/2) + log n | |
T(n) = T(n/2) + n |
∴ T(n) = 2T(n/2) + k, k a constant
Question 23 |
![]() where O(n) stands for order n is:
where O(n) stands for order n is:
O(n) | |
O(n2) | |
O(n3) | |
O(3n2) | |
O(1.5n2) | |
B, C, D and E |
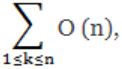
⇒ In this 'n' is constant. So, n is added to n times itself which is O(n2).
Hence, (a) is wrong. And rest (B), (C), (D), (E) are correct.
Question 24 |
Consider the function F(n) for which the pseudo code is given below:
Function F(n)
begin
F1 ← 1
if(n=1) then F ← 3
else For i = 1 to n do
begin
C ← 0
For j = 1 to F(n – 1) do
begin C ← C + 1 end
F1 = F1 * C
end
F = F1
end
[n is a positive integer greater than zero]
(a) Derive a recurrence relation for F(n)
(b) Solve the recurrence relation for a closed form solutions of F(n).
Theory Explanation. |
Question 25 |
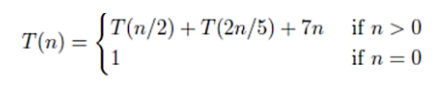
Which one of the following options is correct?
 | |
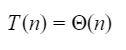 | |
 | |
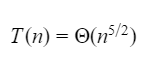 |

Question 26 |

Which algorithm out of the following options uses the least number of comparisons (among the array elements) to sort the above array in ascending order?
Quicksort using the last element as pivot | |
Insertion sort | |
Selection sort | |
Mergesort |
Quick sort(with last element as pivot) → will give the worst case time complexity as O(n^2).
Merge Sort → The merge sort will not depend upon the input order and will give O(nlogn) time complexity.
Insertion Sort → Insertion sort will perform best case time complexity when the input array is in sorted order. If the array is already sorted then the inversion count is 0 and If the array is sorted in reverse order that inversion count is the maximum.
Note: Inversion formal definition is two elements A[i] and A[j] form an inversion if A[i] > A[j] and i < j.
The number of comparisons will not take more than “n” for the given input array.
Selection Sort → Selection sort will not depend upon the input order and will give O(n^2) time complexity.
Question 27 |
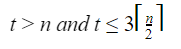 | |
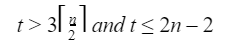 | |
 | |
 |
Let assume n=512
Method-1:
Using standard recursive algorithm:

MaxMin is a recursive algorithm that finds the maximum and minimum of the set of elements {a(i), a(i+1), ..., a(j)}. The situation of set sizes one (i=j) and two (i=j-1) are handled separately. For sets containing more than two elements, the midpoint is determined ( just as in binary search) and two new subproblems are generated. When the maxima and minima of these subproblems are determined, the two maxima are compared and the two minima are compared to achieve the solution for the entire set.
To find the number of element comparisons needed for Maxmin, T(n) represents this number, then the resulting recurrence relation is
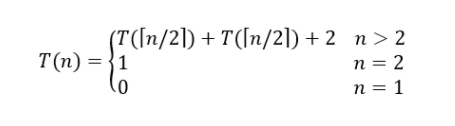
When n is a power of two, n = 2k for some positive integer k, then
T(n)=2T(n/2)+2
=2(2T(n/4)+2)+2
=4T(n/4)+4+2
፧
=2k-1T(2)+1ik-12i
=2k-1+2k-2
=3n/2-2
→ The given example n=512
Apply into 3n/2 -2
= (3*512)/2 -2
= 768-2
= 766
Method-2:
Find the minimum and maximum independently, using n-1 comparisons for each, for a total of 2n-2 comparisons. In fact, at most 3⌊n/2⌋ comparisons are sufficient to find both the minimum and the maximum. The strategy is to maintain the minimum and maximum elements seen thus far. Rather than processing each element of the input by comparing it against the current minimum and maximum, at a cost of 2 comparisons per element, we process elements in pairs. We compare pairs of elements from the input first with each other, and then we compare the smaller to the current minimum and the larger to the current maximum, at a cost of 3 comparisons for every 2 elements.
Setting up initial values for the current minimum and maximum depends on whether n is odd or even. If n is odd, we set both the minimum and maximum to the value of the first element,and then we process the rest of the elements in pairs. If n is even, we perform 1 comparison on the first 2 elements to determine the initial values of the minimum and maximum, and then process the rest of the elements in pairs as in the case for odd n.
Let us analyze the total number of comparisons. If n is odd, then we perform 3⌊n/2⌋ comparisons. If n is even, we perform 1 initial comparison followed by 3(n-2)/2 comparisons, for a total of (3n/2)-2. Thus, in either case, the total number of comparisons is at most 3⌊n/2⌋.
Given an even number of elements. So, 3n/2 -2 comparisons.
= (3*512)/2 -2
= 768-2
= 766
Method-3:
By using Tournament Method:
Step-1: To find the minimum element in the array will take n-1 comparisons.
We are given 512 elements. So, to find the minimum element in the array will take 512-1= 511
Step-2: To find the largest element in the array using the tournament method.
- After the first round of Tournament , there will be exactly n/2 numbers =256 that will lose the round.
- The biggest loser (the largest number) should be among these 256 loosers.To find the largest number will take (n/2)−1 comparisons =256-1 = 255
Total 511+255= 766
Question 28 |
Let f(n), g(n) and h(n) be functions defined for positive inter such that f(n) = O(g(n)), g(n) ≠ O(f(n)), g(n) = O(h(n)), and h(n) = O(g(n)). Which one of the following statements is FALSE?
f(n) + g(n) = O(h(n)) + h(n)) | |
f(n) = O(h(n)) | |
fh(n) ≠ O(f(n)) | |
f(n)h(n) ≠ O(g(n)h(n)) |
So, f(n)g(n) = O(g(n)h(n)) is True.
Hence, (D) is false.
Question 29 |
Arrange the following functions in increasing asymptotic order:
A. n1/3 B. en C. n7/4 D. n log9n E. 1.0000001n
A, D, C, E, B | |
D, A, C, E, B | |
A, C, D, E, B | |
A, C, D, B, E |
n1/3 < n log9 < n7/4 < 1.0000001n < en
Question 30 |
When n = 22k for some k ≥ 0, the recurrence relation
T(n) = √(2)T(n/2) + √n, T(1) = 1evaluates to :
√n (log n + 1) | |
√n log n | |
√n log √n | |
n log √n |

Question 31 |
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only: Kruskal’s algorithm for finding a minimum spanning tree of a weighted graph G with vertices and m edges has the time complexity of:
O(n2) | |
O(mn) | |
O(m+n) | |
O(m log n) | |
O(m2 | |
B, D and E |
→ Where m is no. of edges and n is number of vertices then n = O(m2)
→ O(m logn) < O(mn)
Question 32 |
Choose the correct alternatives (More than one may be correct). The complexity of comparison based sorting algorithms is:
Θ(n logn) | |
Θ(n) | |
Θ(n2) | |
Θ(n√n) | |
Both (A) and (C) |
Question 33 |
The time complexity of computing the transitive closure of a binary relation on a set of n elements is known to be:
O(n) | |
O(n log n) | |
O(n3/2) | |
O(n3) |
For example, if X is a set of airports and x R y means "there is a direct flight from airport x to airport y" (for x and y in X), then the transitive closure of R on X is the relation R+ such that x R+ y means "it is possible to fly from x to y in one or more flights". Informally, the transitive closure gives you the set of all places you can get to from any starting place.
To find the transitive closure of given relation, we can represent the given relation by the graph such that if x R y then there should be directed edge between x and y in a graph. For this graph, we have to apply modified Floyd_Warshall Algorithm to find the transitive closure of the graph.
The time complexity of this algorithm is O(V3) where V is the number of vertices in the given graph. You can take here V as the number of elements is set i.e., N. Therefore time complexity for the given question is O(n3).
