Teaching Aptitude
October 4, 2023Teaching Aptitude
October 4, 2023Data-Structures
|
Question 1
|
Consider the following statements:
I. The smallest element in a max-heap is always at a leaf node.
II. The second largest element in a max-heap is always a child of the root node.
III. A max-heap can be constructed from a binary search tree in Θ(n) time.
IV. A binary search tree can be constructed from a max-heap in Θ(n) time.
Which of the above statements are TRUE?
I. The smallest element in a max-heap is always at a leaf node.
II. The second largest element in a max-heap is always a child of the root node.
III. A max-heap can be constructed from a binary search tree in Θ(n) time.
IV. A binary search tree can be constructed from a max-heap in Θ(n) time.
Which of the above statements are TRUE?
|
I, II and III
|
|
|
II, III and IV
|
|
|
I, III and IV
|
|
|
I, II and IV
|
Question 1 Explanation:
i) TRUE: The smallest element in heap is always a leaf node but depends upon the graph, it may be left or right side of the graph.
(ii) TRUE: The second smallest element in a heap is always a child of root node.
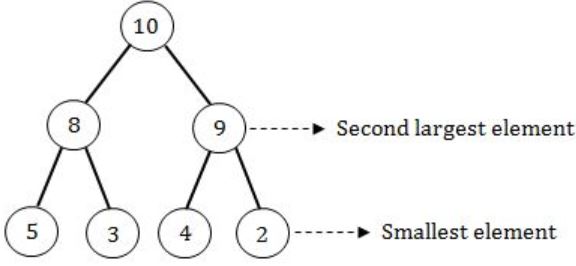
(iii) TRUE: Converting from binary search tree to max heap will take O(n) time as well as O(n) space complexity.
(iv) FALSE: We can’t convert max heap to binary search tree in O(n) time.
(ii) TRUE: The second smallest element in a heap is always a child of root node.

(iii) TRUE: Converting from binary search tree to max heap will take O(n) time as well as O(n) space complexity.
(iv) FALSE: We can’t convert max heap to binary search tree in O(n) time.
Correct Answer: A
Question 1 Explanation:
i) TRUE: The smallest element in heap is always a leaf node but depends upon the graph, it may be left or right side of the graph.
(ii) TRUE: The second smallest element in a heap is always a child of root node.

(iii) TRUE: Converting from binary search tree to max heap will take O(n) time as well as O(n) space complexity.
(iv) FALSE: We can’t convert max heap to binary search tree in O(n) time.
(ii) TRUE: The second smallest element in a heap is always a child of root node.

(iii) TRUE: Converting from binary search tree to max heap will take O(n) time as well as O(n) space complexity.
(iv) FALSE: We can’t convert max heap to binary search tree in O(n) time.
Subscribe
Login
0 Comments
