Data-Structures
October 5, 2023NTA-UGC-NET 2021 Dec & 2022 June Paper-1
October 5, 2023Data-Structures
|
Question 61
|
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?
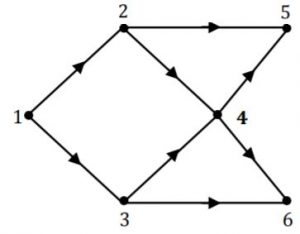
|
1 2 3 4 5 6
|
|
|
1 3 2 4 5 6
|
|
|
1 3 2 4 6 5
|
|
|
3 2 4 1 6 5
|
Question 61 Explanation:
The process to find topological order is,
(i) Go with vertex with indegree 0.
(ii) Then remove that vertex and also remove the edges going from it.
(iii) Repeat again from (i) till every vertex is completed.
Now we can see that in option (D), ‘3’ is given first which is not possible because indegree of vertex ‘3’ is not zero.
Hence option (D) is not topological ordering.
(i) Go with vertex with indegree 0.
(ii) Then remove that vertex and also remove the edges going from it.
(iii) Repeat again from (i) till every vertex is completed.
Now we can see that in option (D), ‘3’ is given first which is not possible because indegree of vertex ‘3’ is not zero.
Hence option (D) is not topological ordering.
Correct Answer: D
Question 61 Explanation:
The process to find topological order is,
(i) Go with vertex with indegree 0.
(ii) Then remove that vertex and also remove the edges going from it.
(iii) Repeat again from (i) till every vertex is completed.
Now we can see that in option (D), ‘3’ is given first which is not possible because indegree of vertex ‘3’ is not zero.
Hence option (D) is not topological ordering.
(i) Go with vertex with indegree 0.
(ii) Then remove that vertex and also remove the edges going from it.
(iii) Repeat again from (i) till every vertex is completed.
Now we can see that in option (D), ‘3’ is given first which is not possible because indegree of vertex ‘3’ is not zero.
Hence option (D) is not topological ordering.
Subscribe
Login
0 Comments
