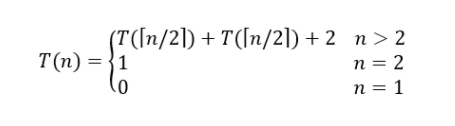Algorithms
October 12, 2023Asymptotic-Complexity
October 12, 2023Algorithms
| Question 22 |
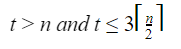 | |
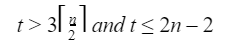 | |
 | |
 |
Let assume n=512
Method-1:
Using standard recursive algorithm:
MaxMin is a recursive algorithm that finds the maximum and minimum of the set of elements {a(i), a(i+1), …, a(j)}. The situation of set sizes one (i=j) and two (i=j-1) are handled separately. For sets containing more than two elements, the midpoint is determined ( just as in binary search) and two new subproblems are generated. When the maxima and minima of these subproblems are determined, the two maxima are compared and the two minima are compared to achieve the solution for the entire set.
To find the number of element comparisons needed for Maxmin, T(n) represents this number, then the resulting recurrence relation is
When n is a power of two, n = 2k for some positive integer k, then
T(n)=2T(n/2)+2
=2(2T(n/4)+2)+2
=4T(n/4)+4+2
፧
=2k-1T(2)+1ik-12i
=2k-1+2k-2
=3n/2-2
→ The given example n=512
Apply into 3n/2 -2
= (3*512)/2 -2
= 768-2
= 766
Method-2:
Find the minimum and maximum independently, using n-1 comparisons for each, for a total of 2n-2 comparisons. In fact, at most 3⌊n/2⌋ comparisons are sufficient to find both the minimum and the maximum. The strategy is to maintain the minimum and maximum elements seen thus far. Rather than processing each element of the input by comparing it against the current minimum and maximum, at a cost of 2 comparisons per element, we process elements in pairs. We compare pairs of elements from the input first with each other, and then we compare the smaller to the current minimum and the larger to the current maximum, at a cost of 3 comparisons for every 2 elements.
Setting up initial values for the current minimum and maximum depends on whether n is odd or even. If n is odd, we set both the minimum and maximum to the value of the first element,and then we process the rest of the elements in pairs. If n is even, we perform 1 comparison on the first 2 elements to determine the initial values of the minimum and maximum, and then process the rest of the elements in pairs as in the case for odd n.
Let us analyze the total number of comparisons. If n is odd, then we perform 3⌊n/2⌋ comparisons. If n is even, we perform 1 initial comparison followed by 3(n-2)/2 comparisons, for a total of (3n/2)-2. Thus, in either case, the total number of comparisons is at most 3⌊n/2⌋.
Given an even number of elements. So, 3n/2 -2 comparisons.
= (3*512)/2 -2
= 768-2
= 766
Method-3:
By using Tournament Method:
Step-1: To find the minimum element in the array will take n-1 comparisons.
We are given 512 elements. So, to find the minimum element in the array will take 512-1= 511
Step-2: To find the largest element in the array using the tournament method.
- After the first round of Tournament , there will be exactly n/2 numbers =256 that will lose the round.
- The biggest loser (the largest number) should be among these 256 loosers.To find the largest number will take (n/2)−1 comparisons =256-1 = 255
Total 511+255= 766
Let assume n=512
Method-1:
Using standard recursive algorithm:
MaxMin is a recursive algorithm that finds the maximum and minimum of the set of elements {a(i), a(i+1), …, a(j)}. The situation of set sizes one (i=j) and two (i=j-1) are handled separately. For sets containing more than two elements, the midpoint is determined ( just as in binary search) and two new subproblems are generated. When the maxima and minima of these subproblems are determined, the two maxima are compared and the two minima are compared to achieve the solution for the entire set.
To find the number of element comparisons needed for Maxmin, T(n) represents this number, then the resulting recurrence relation is
When n is a power of two, n = 2k for some positive integer k, then
T(n)=2T(n/2)+2
=2(2T(n/4)+2)+2
=4T(n/4)+4+2
፧
=2k-1T(2)+1ik-12i
=2k-1+2k-2
=3n/2-2
→ The given example n=512
Apply into 3n/2 -2
= (3*512)/2 -2
= 768-2
= 766
Method-2:
Find the minimum and maximum independently, using n-1 comparisons for each, for a total of 2n-2 comparisons. In fact, at most 3⌊n/2⌋ comparisons are sufficient to find both the minimum and the maximum. The strategy is to maintain the minimum and maximum elements seen thus far. Rather than processing each element of the input by comparing it against the current minimum and maximum, at a cost of 2 comparisons per element, we process elements in pairs. We compare pairs of elements from the input first with each other, and then we compare the smaller to the current minimum and the larger to the current maximum, at a cost of 3 comparisons for every 2 elements.
Setting up initial values for the current minimum and maximum depends on whether n is odd or even. If n is odd, we set both the minimum and maximum to the value of the first element,and then we process the rest of the elements in pairs. If n is even, we perform 1 comparison on the first 2 elements to determine the initial values of the minimum and maximum, and then process the rest of the elements in pairs as in the case for odd n.
Let us analyze the total number of comparisons. If n is odd, then we perform 3⌊n/2⌋ comparisons. If n is even, we perform 1 initial comparison followed by 3(n-2)/2 comparisons, for a total of (3n/2)-2. Thus, in either case, the total number of comparisons is at most 3⌊n/2⌋.
Given an even number of elements. So, 3n/2 -2 comparisons.
= (3*512)/2 -2
= 768-2
= 766
Method-3:
By using Tournament Method:
Step-1: To find the minimum element in the array will take n-1 comparisons.
We are given 512 elements. So, to find the minimum element in the array will take 512-1= 511
Step-2: To find the largest element in the array using the tournament method.
- After the first round of Tournament , there will be exactly n/2 numbers =256 that will lose the round.
- The biggest loser (the largest number) should be among these 256 loosers.To find the largest number will take (n/2)−1 comparisons =256-1 = 255
Total 511+255= 766