DSSSB PGT 2021
October 12, 2023Nielit Scientist-D 2016 march
October 12, 2023UGC NET CS 2014 Dec-Paper-2
|
Question 2
|
A certain tree has two vertices of degree 4, one vertex of degree 3 and one vertex of degree 2. If the other vertices have degree 1, how many vertices are there in the graph ?
|
5
|
|
|
n-3
|
|
|
20
|
|
|
11
|
Question 2 Explanation:
Method-1:
Here, they are clearly mentioned that “certain tree”
The tree contain maximum n-1 edges. Here, ‘n’ is number of vertices.
→ According to the handshaking lemma “sum of degrees of all vertices=2|e|”.
→ Two vertices of degree 4, we can write into (2*4)
→ One vertex of degree 3, we can write into (1*3)
→ One vertex of degree 2, we can write into (1*2).
→ Other vertices(X) have degree 1, we can write into (X*1)
Step-1: (2*4)+(1*3)+(1*2)+(X*1)
=2(X+4-1) [Note: ‘X’ value is not given ]
X=7
Step-2: To find total number of vertices, we are adding X+4 because they already given 4 vertices.
=X+4
=7+4
=11
Method-2:
Draw according to given constraints but it not suitable for very big trees
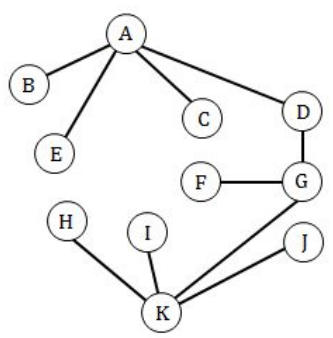
B, C, E, F, H, I, J degree = 1
D degree = 2
A degree = 4
K degree = 4
G degree = 3
Here, they are clearly mentioned that “certain tree”
The tree contain maximum n-1 edges. Here, ‘n’ is number of vertices.
→ According to the handshaking lemma “sum of degrees of all vertices=2|e|”.
→ Two vertices of degree 4, we can write into (2*4)
→ One vertex of degree 3, we can write into (1*3)
→ One vertex of degree 2, we can write into (1*2).
→ Other vertices(X) have degree 1, we can write into (X*1)
Step-1: (2*4)+(1*3)+(1*2)+(X*1)
=2(X+4-1) [Note: ‘X’ value is not given ]
X=7
Step-2: To find total number of vertices, we are adding X+4 because they already given 4 vertices.
=X+4
=7+4
=11
Method-2:
Draw according to given constraints but it not suitable for very big trees

B, C, E, F, H, I, J degree = 1
D degree = 2
A degree = 4
K degree = 4
G degree = 3
Correct Answer: D
Question 2 Explanation:
Method-1:
Here, they are clearly mentioned that “certain tree”
The tree contain maximum n-1 edges. Here, ‘n’ is number of vertices.
→ According to the handshaking lemma “sum of degrees of all vertices=2|e|”.
→ Two vertices of degree 4, we can write into (2*4)
→ One vertex of degree 3, we can write into (1*3)
→ One vertex of degree 2, we can write into (1*2).
→ Other vertices(X) have degree 1, we can write into (X*1)
Step-1: (2*4)+(1*3)+(1*2)+(X*1)
=2(X+4-1) [Note: ‘X’ value is not given ]
X=7
Step-2: To find total number of vertices, we are adding X+4 because they already given 4 vertices.
=X+4
=7+4
=11
Method-2:
Draw according to given constraints but it not suitable for very big trees

B, C, E, F, H, I, J degree = 1
D degree = 2
A degree = 4
K degree = 4
G degree = 3
Here, they are clearly mentioned that “certain tree”
The tree contain maximum n-1 edges. Here, ‘n’ is number of vertices.
→ According to the handshaking lemma “sum of degrees of all vertices=2|e|”.
→ Two vertices of degree 4, we can write into (2*4)
→ One vertex of degree 3, we can write into (1*3)
→ One vertex of degree 2, we can write into (1*2).
→ Other vertices(X) have degree 1, we can write into (X*1)
Step-1: (2*4)+(1*3)+(1*2)+(X*1)
=2(X+4-1) [Note: ‘X’ value is not given ]
X=7
Step-2: To find total number of vertices, we are adding X+4 because they already given 4 vertices.
=X+4
=7+4
=11
Method-2:
Draw according to given constraints but it not suitable for very big trees

B, C, E, F, H, I, J degree = 1
D degree = 2
A degree = 4
K degree = 4
G degree = 3
Subscribe
Login
0 Comments
