UGC NET CS 2007 June-Paper-2
October 13, 2023Algorithms
October 13, 2023Algorithms
|
Question 28
|
The graph shown below 8 edges with distinct integer edge weights. The minimum spanning tree (MST) is of weight 36 and contains the edges: {(A, C), (B, C), (B, E), (E, F), (D, F)}. The edge weights of only those edges which are in the MST are given in the figure shown below. The minimum possible sum of weights of all 8 edges of this graph is ______________.
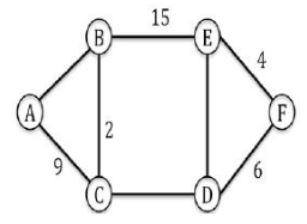
|
69
|
|
|
70
|
|
|
71
|
|
|
72
|
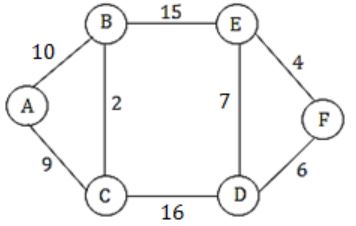
⇒ Total sum = 10 + 9 + 2 + 15 + 7 + 16 + 4 + 6 = 69
–> First we compare A-C and A-B we find 9 at A-C it means A-B must greater than A-C and for minimum possible greater value than 9 will be 10
-> Second we compare B-E and C-D in which we select B-E is 15 which C-D possible weight 16.
-> Third, we compare E-D and F-D in which we select F-D 6 means E-D must be greater than 6 so possible value greater than 6 is 7 .
Note: Add First+Second+Third=(A-B=10)+(C-D=16)+(E-D=7)

⇒ Total sum = 10 + 9 + 2 + 15 + 7 + 16 + 4 + 6 = 69
–> First we compare A-C and A-B we find 9 at A-C it means A-B must greater than A-C and for minimum possible greater value than 9 will be 10
-> Second we compare B-E and C-D in which we select B-E is 15 which C-D possible weight 16.
-> Third, we compare E-D and F-D in which we select F-D 6 means E-D must be greater than 6 so possible value greater than 6 is 7 .
Note: Add First+Second+Third=(A-B=10)+(C-D=16)+(E-D=7)
