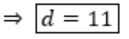Software-Engineering
October 15, 2023Functional-Dependency
October 15, 2023RSA-algorithm
| Question 1 |
In a RSA cryptosystem, a participant A uses two prime numbers p = 13 and q = 17 to generate her public and private keys. If the public key of A is 35, then the private key of A is _________.
| 11 | |
| 12 | |
| 13 | |
| 14 |
Question 1 Explanation:
Correct Answer is 11.
Given, p=13, q=17, e=35 (Public key), d=? (Private key)
As per RSA Algorithm; following steps:
Step 1: Find n = p×q = 13×17 = 221
Step 2: Find ∅(n) = (p-1)×(q-1) = 12×16 = 192
Step 3: d×e mod ∅(n) = 1 ⇒ (d = e(-1) mod ∅(n))
or
d×e = 1 mod ∅(n)
⇒ d×35 mod 192 = 1
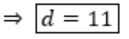
Given, p=13, q=17, e=35 (Public key), d=? (Private key)
As per RSA Algorithm; following steps:
Step 1: Find n = p×q = 13×17 = 221
Step 2: Find ∅(n) = (p-1)×(q-1) = 12×16 = 192
Step 3: d×e mod ∅(n) = 1 ⇒ (d = e(-1) mod ∅(n))
or
d×e = 1 mod ∅(n)
⇒ d×35 mod 192 = 1
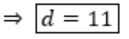
Correct Answer: A
Question 1 Explanation:
Correct Answer is 11.
Given, p=13, q=17, e=35 (Public key), d=? (Private key)
As per RSA Algorithm; following steps:
Step 1: Find n = p×q = 13×17 = 221
Step 2: Find ∅(n) = (p-1)×(q-1) = 12×16 = 192
Step 3: d×e mod ∅(n) = 1 ⇒ (d = e(-1) mod ∅(n))
or
d×e = 1 mod ∅(n)
⇒ d×35 mod 192 = 1
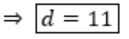
Given, p=13, q=17, e=35 (Public key), d=? (Private key)
As per RSA Algorithm; following steps:
Step 1: Find n = p×q = 13×17 = 221
Step 2: Find ∅(n) = (p-1)×(q-1) = 12×16 = 192
Step 3: d×e mod ∅(n) = 1 ⇒ (d = e(-1) mod ∅(n))
or
d×e = 1 mod ∅(n)
⇒ d×35 mod 192 = 1
Subscribe
Login
0 Comments