Boolean-Algebra
October 19, 2023GATE 2010
October 19, 2023Boolean-Algebra
|
Question 9
|
Consider the following Boolean expression for F:
F(P, Q, R, S) = PQ + P'QR + P'QR'S
The minimal sum-of-products form of F is
 |
|
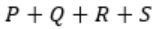 |
|
 |
|
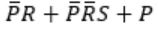 |
Question 9 Explanation:
PQ + P’QR + P’QR’S
= Q(P+P’R) + P’QR’S
= Q(P+R) + P’QR’S
= QP + QR + P’QR’S
= QP + Q(R + P’R’S)
= QP + Q( R + P’S)
= QP + QR + QP’S
= Q(P+P’S) + QR
= Q(P+S)+ QR
= QP + QS + QR
= Q(P+P’R) + P’QR’S
= Q(P+R) + P’QR’S
= QP + QR + P’QR’S
= QP + Q(R + P’R’S)
= QP + Q( R + P’S)
= QP + QR + QP’S
= Q(P+P’S) + QR
= Q(P+S)+ QR
= QP + QS + QR
Correct Answer: A
Question 9 Explanation:
PQ + P’QR + P’QR’S
= Q(P+P’R) + P’QR’S
= Q(P+R) + P’QR’S
= QP + QR + P’QR’S
= QP + Q(R + P’R’S)
= QP + Q( R + P’S)
= QP + QR + QP’S
= Q(P+P’S) + QR
= Q(P+S)+ QR
= QP + QS + QR
= Q(P+P’R) + P’QR’S
= Q(P+R) + P’QR’S
= QP + QR + P’QR’S
= QP + Q(R + P’R’S)
= QP + Q( R + P’S)
= QP + QR + QP’S
= Q(P+P’S) + QR
= Q(P+S)+ QR
= QP + QS + QR
