Question 9491 – GATE 2004
October 29, 2023NTA UGC NET JUNE-2023 Paper-2
October 29, 2023UGC NET CS 2015 Dec- paper-2
| Question 4 |
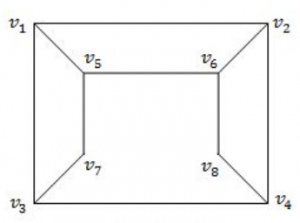
Consider the graph given below: The two distinct sets of vertices, which make the graph bipartite are:
| (v 1 , v 4 , v 6 ); (v 2 , v 3 , v 5 , v 7 , v 8 ) | |
| (v 1 , v 7 , v 8 ); (v 2 , v 3 , v 5 , v 6 ) | |
| (v 1 , v 4 , v 6 , v 7 ); (v 2 , v 3 , v 5 , v 8 ) | |
| (v 1 , v 4 , v 6 , v 7 , v 8 ); (v 2 , v 3 , v 5 ) |
Question 4 Explanation:
A bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
→ The two sets U and V may be thought of as a coloring of the graph with two colors.
Option A: FALSE because V 5 , V 7 and V 3 are adjacent. So, it not not bipartite graph.

Option-B FALSE because V 5 , V 6 and V 2 are adjacent. So, it not not bipartite graph.

Option-C TRUE because it follows properties of bipartied and no two colours are adjacent.

Option-D FALSE because because V 4 , V 6 and V 8 are adjacent. So, it not not bipartite graph.

→ The two sets U and V may be thought of as a coloring of the graph with two colors.
Option A: FALSE because V 5 , V 7 and V 3 are adjacent. So, it not not bipartite graph.
Option-B FALSE because V 5 , V 6 and V 2 are adjacent. So, it not not bipartite graph.
Option-C TRUE because it follows properties of bipartied and no two colours are adjacent.
Option-D FALSE because because V 4 , V 6 and V 8 are adjacent. So, it not not bipartite graph.
Correct Answer: C
Question 4 Explanation:
A bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
→ The two sets U and V may be thought of as a coloring of the graph with two colors.
Option A: FALSE because V 5 , V 7 and V 3 are adjacent. So, it not not bipartite graph.

Option-B FALSE because V 5 , V 6 and V 2 are adjacent. So, it not not bipartite graph.

Option-C TRUE because it follows properties of bipartied and no two colours are adjacent.

Option-D FALSE because because V 4 , V 6 and V 8 are adjacent. So, it not not bipartite graph.

→ The two sets U and V may be thought of as a coloring of the graph with two colors.
Option A: FALSE because V 5 , V 7 and V 3 are adjacent. So, it not not bipartite graph.
Option-B FALSE because V 5 , V 6 and V 2 are adjacent. So, it not not bipartite graph.
Option-C TRUE because it follows properties of bipartied and no two colours are adjacent.
Option-D FALSE because because V 4 , V 6 and V 8 are adjacent. So, it not not bipartite graph.
