Question 11589 – Functional-Dependency
February 29, 2024Question 15864 – STQC-NIELIT SC-B 2021
February 29, 2024Question 14220 – Probability-and-statistics
A sender (S) transmits a signal, which can be one of the two kinds: H and L with probabilities 0.1 and 0.9 respectively, to a receiver (R).
In the graph below, the weight of edge (u, v) is the probability of receiving v when u is transmitted, where u, v ∈ {H, L}. For example, the probability that the received signal is L given the transmitted signal was H, is 0.7.
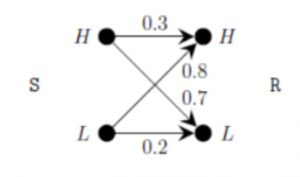
If the received signal is H, the probability that the transmitted signal was H (rounded to 2 decimal places) is _______
Correct Answer: A
Bayes theorem:
Probability of event A happening given that event B has already happened is
P(A/B) = P(B/A)*P(A) / P(B)
Here, it is asked that P( H transmitted / H received).
S can send signal to H with 0.1 probability, S can send signal to L with 0.9 probability.
The complete diagram can be
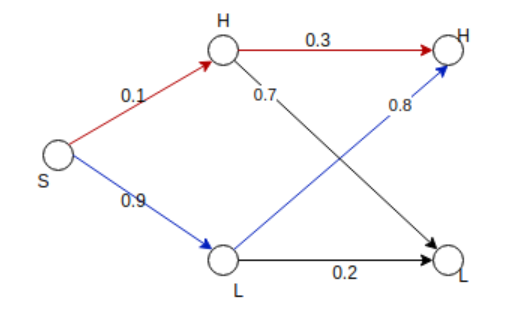
Probability that H Transmitted (H_t) given that H received (H_r)is
P( H_t / H_r) = P( H_r/ H_t) * P(H_t) / P(H_r)
P(H-r) = probability that H received = P( H received from H)+ P(H received from L)
It can be observed from the graph that H can receive in two ways (S to H to H) and (S to L to H)
The P(H_r) = 0.1*0.3 + 0.9*0.8= 0.03+0.72 = 0.75
P(H_received given that H_transmitted) =0.3
P(H transmitted ) = 0.1 i.e.
P( H_t / H_r) = P( H_r/ H_t) * P(H_t) / P(H_r)
= 0.3*0.1 / 0.75 = 0.04
