Question 8517 – Data-Structures
April 17, 2024Question 8138 – Data-Structures
April 17, 2024Question 8136 – Data-Structures
A complete binary min-heap is made by including each integer in [1, 1023] exactly once. The depth of a node in the heap is the length of the path from the root of the heap to that node. Thus, the root is at depth 0. The maximum depth at which integer 9 can appear is _________.
Correct Answer: A
Question 32 Explanation:
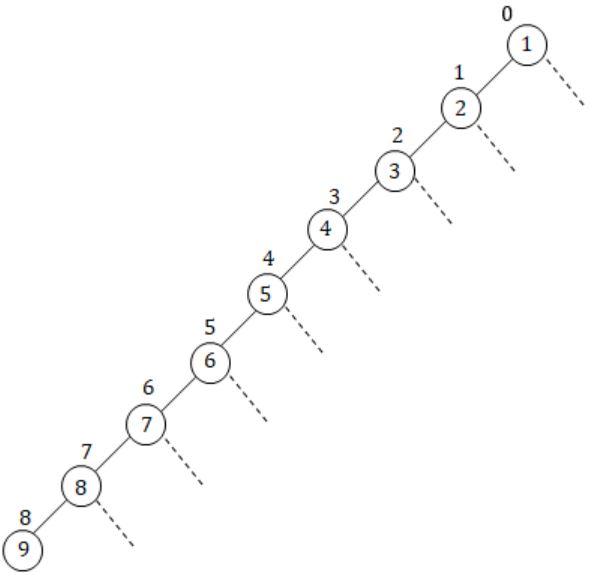
This is not possible because it violates a property of complete binary tree.
We have total [0, 1023] elements. It means that

∴ 20 + 21 + 22 + ⋯ + 2k = 1024
Add if 1(2(k+1)-1)/(2-1) [using formula for sum of k terms k+1 in G.P]
= 2(k+1) – 1 = 1024 – 1 = 1023
∴ The level ‘9’ at the depth of 8.
Actually we have 1023 elements, we can achieve a complete binary min heap of depth 9, which would cover all 1023 elements, but the max depth of node 9 can be only be 8.
8
9
10
11
