Question 8856 – Compiler-Design
May 4, 2024Question 8816 – Theory-of-Computation
May 4, 2024Question 8857 – Compiler-Design
For the grammar below, a partial LL(1) parsing table is also presented along with the grammar. Entries that need to be filled are indicated as E1, E2, and E3. ε is the empty string, $ indicates end of input, and, | separates alternate right hand sides of productions.
S → aAbB | bAaB | ε A → S B → S
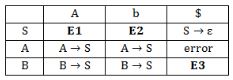
The appropriate entries for E1, E2, and E3 are
Correct Answer: C
Question 17 Explanation:
The entries in E1, E2 and E3 is related to S and B, so we have to take only those production which have S and B in LHS.
S→ aAbB | bAaB | ε
The production S→ aAbB will go under column FIRST (aAbB) = a, so S→ aAbB will be in E1.
S→ bAaB will go under column FIRST(bAaB) = b, so S→ bAaB will be in E2.
S→ ε will go under FOLLOW (S) = FOLLOW(B) = {a, b, $ } , So S→ ε will go in E1, E2 and under column of $.
So E1 will have: S→ aAbB and S→ ε.
E2 will have S→ bAaB and S→ ε.
Now, B→ S will go under FIRST (S) = {a, b, ε}
Since FIRST(S) = ε so B→ S will go under FOLLOW (B) = {a, b, $}
So E3 will contain B→ S.
S→ aAbB | bAaB | ε
The production S→ aAbB will go under column FIRST (aAbB) = a, so S→ aAbB will be in E1.
S→ bAaB will go under column FIRST(bAaB) = b, so S→ bAaB will be in E2.
S→ ε will go under FOLLOW (S) = FOLLOW(B) = {a, b, $ } , So S→ ε will go in E1, E2 and under column of $.
So E1 will have: S→ aAbB and S→ ε.
E2 will have S→ bAaB and S→ ε.
Now, B→ S will go under FIRST (S) = {a, b, ε}
Since FIRST(S) = ε so B→ S will go under FOLLOW (B) = {a, b, $}
So E3 will contain B→ S.
E1: S → aAbB,A → S
E2: S → bAaB,B→S
E3: B → S
E2: S → bAaB,B→S
E3: B → S
E1: S → aAbB,S→ ε
E2: S → bAaB,S → ε
E3: S → ε
E2: S → bAaB,S → ε
E3: S → ε
E1: S → aAbB,S → ε
E2: S → bAaB,S→ε
E3: B → S
E2: S → bAaB,S→ε
E3: B → S
E1: A → S,S →ε
E2: B → S,S → ε
E3: B →S
E2: B → S,S → ε
E3: B →S
Subscribe
Login
0 Comments
