Question 8144 – Theory-of-Computation
June 2, 2024Question 10322 – Computer-Organization
June 3, 2024Question 8731 – Engineering-Mathematics
There are two elements x, y in a group (G,∗) such that every element in the group can be written as a product of some number of x’s and y’s in some order. It is known that
x * x = y * y = x * y * x = y * x * y * x = e
where e is the identity element. The maximum number of elements in such a group is ________.
Correct Answer: A
Question 126 Explanation:
We know
a*a-1 = e
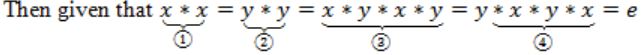
1. x*x = e So x-1 is x ⇒ x is element of Group
2. y*y = e So y-1 = y ⇒ y is element of Group
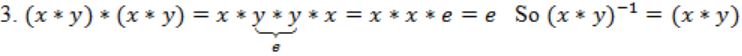
4. (y*x)*(y*x) = x*y*y*x = x*x*e = e So (y*x)-1 = (y*x)
In ③, ④
x*y, y*x has same inverse, there should be unique inverse for each element.
x*y = y*x (even with cumulative law, we can conclude)
So {x, y, e, x*y} are element of Group.
a*a-1 = e
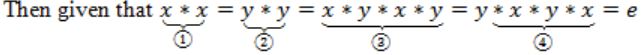
1. x*x = e So x-1 is x ⇒ x is element of Group
2. y*y = e So y-1 = y ⇒ y is element of Group
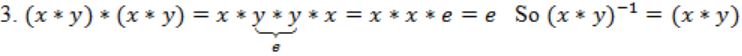
4. (y*x)*(y*x) = x*y*y*x = x*x*e = e So (y*x)-1 = (y*x)
In ③, ④
x*y, y*x has same inverse, there should be unique inverse for each element.
x*y = y*x (even with cumulative law, we can conclude)
So {x, y, e, x*y} are element of Group.
4
5
6
7
Subscribe
Login
0 Comments