Engineering-Mathematics
August 15, 2024SQL
August 16, 2024Engineering-Mathematics
| Question 15 |
Find the inverse of the matrix
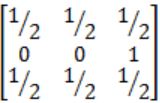 | |
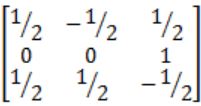 | |
 | |
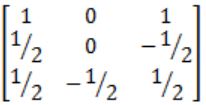 |
Question 15 Explanation:
Using eigen values, the characteristic equation we get is,
-λ3 + 2λ2 – 2 = 0
Using Cayley-Hamiltonian theorem
-A3 + 2A2 – 2I = 0
So, A-1 = 1/2 (2A – A2)
Solving we get,

-λ3 + 2λ2 – 2 = 0
Using Cayley-Hamiltonian theorem
-A3 + 2A2 – 2I = 0
So, A-1 = 1/2 (2A – A2)
Solving we get,

Correct Answer: B
Question 15 Explanation:
Using eigen values, the characteristic equation we get is,
-λ3 + 2λ2 – 2 = 0
Using Cayley-Hamiltonian theorem
-A3 + 2A2 – 2I = 0
So, A-1 = 1/2 (2A – A2)
Solving we get,

-λ3 + 2λ2 – 2 = 0
Using Cayley-Hamiltonian theorem
-A3 + 2A2 – 2I = 0
So, A-1 = 1/2 (2A – A2)
Solving we get,


