Linear-Algebra
Question 1 |
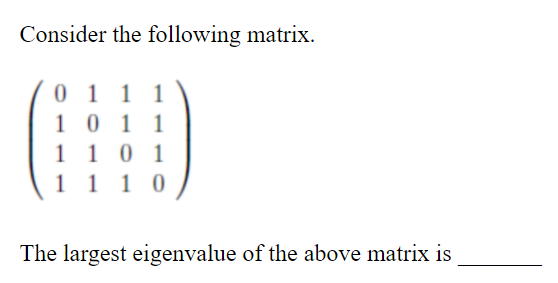
3 |

Question 2 |
The eigen vector(s) of the matrix
is (are)
(0,0,α ) | |
(α,0,0) | |
(0,0,1) | |
(0,α,0) | |
Both B and D |
So the question as has
(A - λI)X = 0
AX = 0
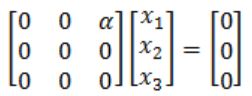
What x1, x2, x3 are suitable?
Which means:
x1 times column 1 + x2 times column 2 + x3 times column 3 = zero vector
Since α is not equal to zero, so x3 must be necessarily zero to get zero vector.
Hence, only (B) and (D) satisfies.
Question 3 |
If  the matrix A4, calculated by the use of Cayley-Hamilton theorem or otherwise, is _________
the matrix A4, calculated by the use of Cayley-Hamilton theorem or otherwise, is _________
A4 = I |
(1-λ) (-1-λ) (i-λ) (-i-λ)
= (λ2-1) (λ2+1)
= λ4-1
Characteristic equation is λ4-1 = 0.
According to Cayley-Hamilton theorem, every matrix satisfies its own characteristic equation, so
A4 = I
Question 4 |
Let A and B be real symmetric matrices of size n × n. Then which one of the following is true?
AA′ = 1 | |
A = A-1 | |
AB = BA | |
(AB)' = BA |

Question 5 |
The tank of matrix ![]() is:
is:
0 | |
1 | |
2 | |
3 |

Question 6 |
In a compact single dimensional array representation for lower triangular matrices (i.e all the elements above the diagonal are zero) of size n × n, non-zero elements (i.e elements of the lower triangle) of each row are stored one after another, starting from the first row, the index of the (i, j)th element of the lower triangular matrix in this new representation is:
i + j | |
i + j - 1 | |
j + i(i-1)/2 | |
i + j(j-1)/2 |
If we assume array index starting from 1 then, ith row contains i number of non-zero elements. Before ith row there are (i-1) rows, (1 to i-1) and in total these rows has 1+2+3......+(i-1) = i(i-1)/2 elements.
Now at ith row, the jth element will be at j position.
So the index of (i, j)th element of lower triangular matrix in this new representation is
j = i(i-1)/2
Question 7 |
Find the inverse of the matrix 
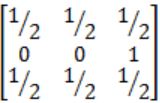 | |
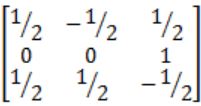 | |
 | |
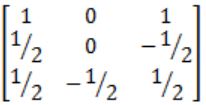 |
-λ3 + 2λ2 - 2 = 0
Using Cayley-Hamiltonian theorem
-A3 + 2A2 - 2I = 0
So, A-1 = 1/2 (2A - A2)
Solving we get,

Question 8 |
In the interval [0, π] the equation x = cos x has
No solution | |
Exactly one solution | |
Exactly two solutions | |
An infinite number of solutions |
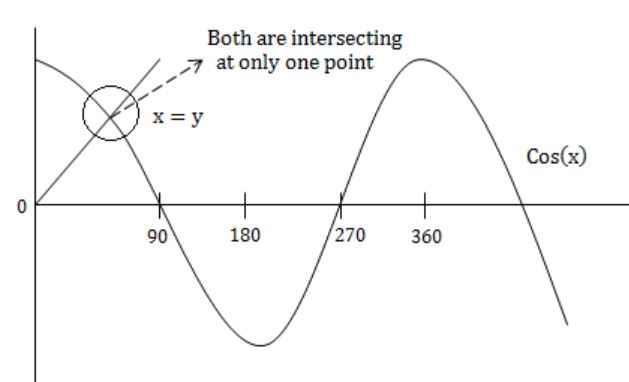
x & cos(x) are intersecting at only one point.
Question 9 |
The rank of the following (n + 1)×(n+1) matrix, where a is a real number is

1 | |
2 | |
n | |
Depends on the value of a |

Question 10 |
Let A be the set of all non-singular matrices over real number and let* be the matrix multiplication operation. Then
A is closed under* but < A, *> is not a semigroup | |
Question 11 |
Let A and B be two n×n matrices over real numbers. Let rank(M) and det(M) denote the rank and determinant of a matrix M, respectively. Consider the following statements,
- I. rank(AB) = rank(A) rank(B)
II. det(AB) = det(A) det(B)
III. rank(A + B) ≤ rank(A) + rank(B)
IV. det(A + B) ≤ det(A) + det(B)
Which of the above statements are TRUE?
I and II only
| |
I and IV only | |
III and IV only | |
II and III only
|
Rank is the number of independent rows(vectors) of a matrix. On product of two matrices, the combined rank is more than the sum of individual matrices (subtracted with the order n)
det(AB) = det(A)∙det(B) as the magnitude remains same for the matrices after multiplication.
Note: We can just take a 2x2 matrix and check the options.
Question 12 |
Let Ax = b be a system of linear equations where A is an m × n matrix and b is a m × 1 column vector and X is a n × 1 column vector of unknowns. Which of the following is false?
The system has a solution if and only if, both A and the augmented matrix [A b] have the same rank.
| |
If m < n and b is the zero vector, then the system has infinitely many solutions. | |
If m = n and b is non-zero vector, then the system has a unique solution. | |
The system will have only a trivial solution when m = n, b is the zero vector and rank (A) = n. |
→ Solution can be depends on rank of matrix A and matrix [A B].
→ If rank[A] = rank[A B] then it can have solution otherwise no solution.
Question 13 |
The matrices ![]() and
and ![]() commute under multiplication
commute under multiplication
if a = b or θ = nπ, is an integer | |
always | |
never | |
if a cos θ ≠ b sin θ |
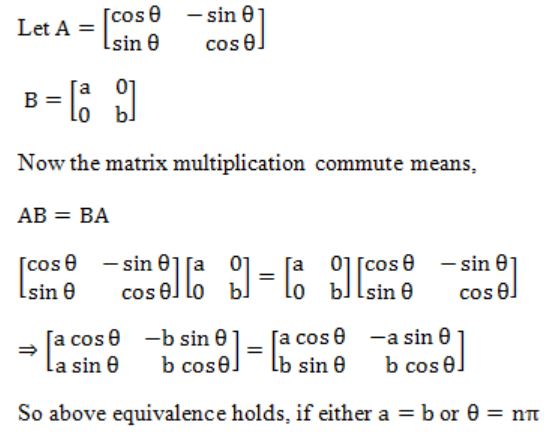
Question 14 |
Let ![]() and
and ![]() be two matrices such that AB = I. Let
be two matrices such that AB = I. Let ![]() and CD = 1. Express the elements of D in terms of the elements of B.
and CD = 1. Express the elements of D in terms of the elements of B.
Theory Explanation. |
Question 15 |
I. X is invertible.
II. Determinant of X is non-zero.
Which one of the following is TRUE?
I implies II; II does not imply I. | |
II implies I; I does not imply II. | |
I and II are equivalent statements. | |
I does not imply II; II does not imply I. |
That means we can also say that determinant of X is non-zero.
Question 16 |
Consider the following matrix:
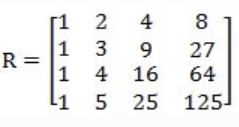
The absolute value of the product of Eigen values of R is ______.
12 | |
17 | |
10 | |
8 |

Question 17 |
The determinant of the matrix is  is:
is:
11 | |
-48 | |
0 | |
-24 |
Question 18 |
Let A = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identify matrix. Then AI12 is such that its first
row is the same as its second row | |
row is the same as the second row of A | |
column is the same as the second column of A | |
row is all zero |

So, we can see that column 1 and 2 got interchanged.
Question 19 |
Consider the following set of equations
x + 2y = 5
4x + 8y = 12
3x + 6y + 3z = 15
This set
has unique solution | |
has no solutions | |
has finite number of solutions | |
has infinite number of solutions |

Question 20 |
The rank of the matrix given below is:
1 4 8 7
0 0 3 0
4 2 3 1
3 12 24 2
3 | |
1 | |
2 | |
4 |

Question 21 |
Consider the following determinant 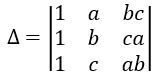
Which of the following is a factor of Δ?
a+b | |
a-b | |
a+b+c | |
abc |

Question 22 |
Derive the expression for the number of expressions required to solve a system of linear equations in n unknowns using the Gaussian Elimination Method. Assume that one operation refers to a multiplication followed by an addition.
Theory Explanation. |
Question 23 |
An n x n array v is defined as follows:
v[i,j] = i-j for all i,j, 1 ≤ i ≤ n, 1 ≤ j ≤ n
The sum of the elements of the array v is
0 | |
n -1 | |
n2 - 3n + 2 | |
n2 (n+1)/2 |
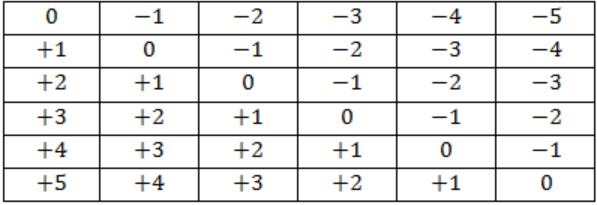
Add ith row and jth column if we zero, apply to all row and their corresponding column the total becomes zero.
Question 24 |
The determinant of the matrix is

is:
4 | |
0 | |
15 | |
20 |
Question 25 |
Consider the following statements:
- S1: The sum of two singular n × n matrices may be non-singular
S2: The sum of two n × n non-singular matrices may be singular.
Which of the following statements is correct?
S1 and S2 are both true | |
S1 is true, S2 is false | |
S1 is false, S2 is true | |
S1 and S2 are both false |

Question 26 |
The rank of the matrix ![]() is
is
4 | |
2 | |
1 | |
0 |
Question 27 |
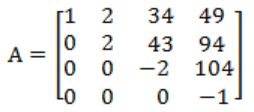
(a) Obtain the eigen values of the matrix
(b) Determine whether each of the following is a tautology, a contradiction, or neither (“∨” is disjunction, “∧” is conjunction, “→” is implication, “¬” in negation, and “↔” is biconditional (if and only if).
(i) A ↔ (A ∨ A) (ii) (A ∨ B) → B (iii) A ∧(¬(A ∨ B)
Theory Explanation is given below. |
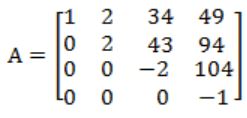
Eigen value of upper/ lower triangular matrix are the diagonal elements of matrix.
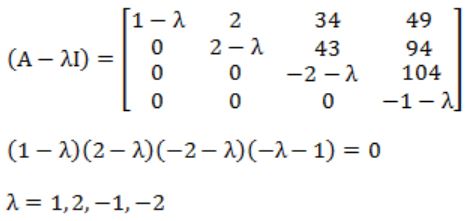
(b) (i) A↔(A∨A): This can tells that if A then (A or A)and if (A or A) then A. It represents result as a tautology.
(ii) (A∨B)→B: This is neither tautology nor contradiction.
(iii) A∧(¬(A∨B)): here when A is true then (¬(A∨B)) is false, then it results contradiction.
Question 28 |
The largest eigenvalue of A is ________
3 | |
4 | |
5 | |
6 |
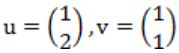
→ Correction in Explanation:
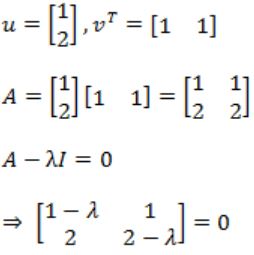
⇒ (1 - λ)(2 - λ) - 2 = 0
⇒ λ2 - 3λ=0
λ = 0, 3
So maximum is 3.
Question 29 |
Assume that multiplying a matrix G1 of dimension p×q with another matrix G2 of dimension q×r requires pqr scalar multiplications. Computing the product of n matrices G1G2G3…Gn can be done by parenthesizing in different ways. Define GiGi+1 as an explicitly computed pair for a given parenthesization if they are directly multiplied. For example, in the matrix multiplication chain G1G2G3G4G5G6 using parenthesization(G1(G2G3))(G4(G5G6)), G2G3 and G5G6 are the only explicitly computed pairs.
Consider a matrix multiplication chain F1F2F3F4F5, where matrices F1, F2, F3, F4 and F5 are of dimensions 2×25, 25×3, 3×16, 16×1 and 1×1000, respectively. In the parenthesization of F1F2F3F4F5 that minimizes the total number of scalar multiplications, the explicitly computed pairs is/ are
F1F2 and F3F4 only
| |
F2F3 only | |
F3F4 only | |
F1F2 and F4F5 only
|
→ Optimal Parenthesization is:
((F1(F2(F3 F4)))F5)
→ But according to the problem statement we are only considering F3, F4 explicitly computed pairs.
Question 30 |
Consider Guwahati (G) and Delhi (D) whose temperatures can be classified as high (H), medium (M) and low (L). Let P(HG) denote the probability that Guwahati has high temperature. Similarly, P(MG) and P(LG) denotes the probability of Guwahati having medium and low temperatures respectively. Similarly, we use P(HD), P(MD) and P(LD) for Delhi.
The following table gives the conditional probabilities for Delhi’s temperature given Guwahati’s temperature.
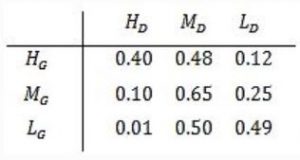
Consider the first row in the table above. The first entry denotes that if Guwahati has high temperature (HG) then the probability of Delhi also having a high temperature (HD) is 0.40; i.e., P(HD ∣ HG) = 0.40. Similarly, the next two entries are P(MD ∣ HG) = 0.48 and P(LD ∣ HG) = 0.12. Similarly for the other rows.
If it is known that P(HG) = 0.2, P(MG) = 0.5, and P(LG) = 0.3, then the probability (correct to two decimal places) that Guwahati has high temperature given that Delhi has high temperature is _______ .
0.60 | |
0.61 | |
0.62 | |
0.63 |
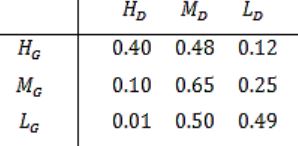
The first entry denotes that if Guwahati has high temperature (HG ) then the probability that Delhi also having a high temperature (HD ) is 0.40.
P (HD / HG ) = 0.40
We need to find out the probability that Guwahati has high temperature.
Given that Delhi has high temperature (P(HG / HD )).

P (HD / HG ) = P(HG ∩ HD ) / P(HD )
= 0.2×0.4 / 0.2×0.4+0.5×0.1+0.3×0.01
= 0.60
Question 31 |
P: Set of Rational numbers (positive and negative)
Q: Set of functions from {0, 1} to N
R: Set of functions from N to {0, 1}
S: Set of finite subsets of N
Which of the above sets are countable?
Q and S only | |
P and S only | |
P and R only | |
P, Q and S only |
Set of functions from {0,1} to N is countable as it has one to one correspondence to N.
Set of functions from N to {0,1} is uncountable, as it has one to one correspondence to set of real numbers between (0 and 1).
Set of finite subsets of N is countable.
Question 32 |
 .
. Consider the following statements.
(I)P does not have an inverse
(II)P has a repeated eigenvalue
(III)P cannot be diagonalized
Which one of the following options is correct?
Only I and III are necessarily true | |
Only II is necessarily true | |
Only I and II are necessarily true | |
Only II and III are necessarily true |

Though the multiple of a vector represents same vector, and each eigen vector has distinct eigen value, we can conclude that ‘p’ has repeated eigen value.
If the unique eigen value corresponds to an eigen vector e, but the repeated eigen value corresponds to an entire plane, then the matrix can be diagonalized, using ‘e’ together with any two vectors that lie in plane.
But, if all eigen values are repeated, then the matrix cannot be diagonalized unless it is already diagonal.
So (III) holds correct.
A diagonal matrix can have inverse, So (I) is false.
Then (II) and (III) are necessarily True.
Question 33 |
The number of integer-triples (i.j.k) with 1 ≤ i.j.k ≤ 300 such that i + j + k is divisible by 3 is ________
Fill in the blanks. |
Question 34 |
4 |
Question 35 |

There exists a bijection from S1to S2. | |
There does not exist a bijection from S1to S2. | |
There exists a surjection from S1to S2. | |
There does not exist an injunction from S1to S2. |
The number of functions from a set A to set B is |B|^|A|.
S2: |B|= 3, |A|= n^2-1 +1 = n^2.
we have number of functions 3^(n^2).
S1: there are n*n positions in a matrix of size nxn. Each can be filled with either 0 or 1 or 2 i,e, in 3^(n^2)
As there are equal number of elements on both sides, S1->S2 can be one one , onto as well bijection
Question 36 |

where tr() represents the trace of a matrix. Which one of the following holds?
Statement 1 is correct and Statement 2 is wrong. | |
Statement 1 is wrong and Statement 2 is correct. | |
Both Statement 1 and Statement 2 are correct. | |
Both Statement 1 and Statement 2 are wrong. |
(In exam point of view, you can just consider small example and conclude).
So trace of AB = trace of BA
As well
Trace of CD = trace of DC
Question 37 |

 | |
 | |
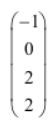 | |
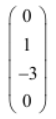 |


Question 38 |
What values of x, y and z satisfy the following system of linear equations?

x = 6, y = 3, z = 2 | |
x = 12, y = 3, z = -4 | |
x = 6, y = 6, z = -4 | |
x = 12, y = -3, z = 0 |
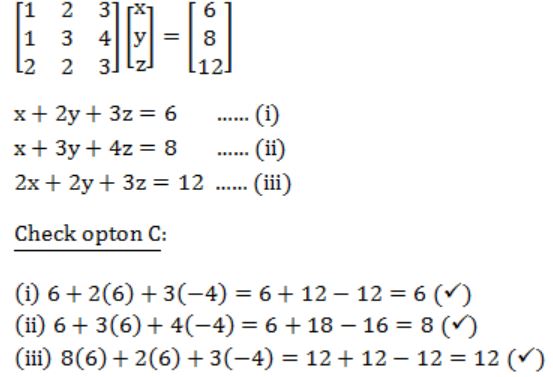
Question 39 |
Let A be an Let A be an n × n matrix of the following form.

What is the value of the determinant of A?
 | |
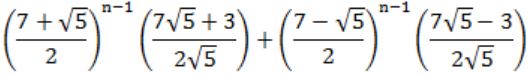 | |
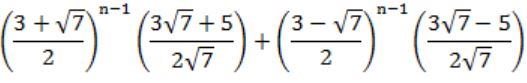 | |
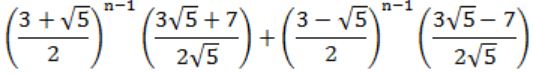 |
Find its determinant, Determinant = 3.
Now check options, by putting n=1, I am getting following results,
A) 5
B) 7
C) 3
D) 3
(A), (B) can't be the answer.
Now, check for n=2, Determinant = 9-1 = 8.
Put n=2 in (C), (D)
C) 7
D) 8
So, (D) is the answer.
