GATE 2003
February 1, 2024Question 8492 – Operator
February 1, 2024GATE 1996
| Question 1 |
Let A and B be sets and let Ac and Bc denote the complements of the sets A and B. The set (A – B) ∪ (B – A) ∪ (A∩B) is equal to
| A ∪ B | |
| Ac ∪ Bc | |
| A ∩ B | |
| Ac ∩ Bc |
Question 1 Explanation:
(A – B) ∪ (B – A) ∪ (A∩B)

(A – B) = 1
(B – A) = 2
(A∩B) = 3
A∪B = (1∪2∪3)
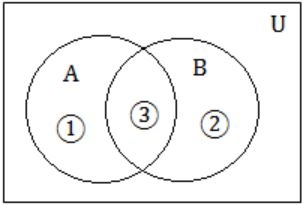
(A – B) = 1
(B – A) = 2
(A∩B) = 3
A∪B = (1∪2∪3)
(A – B) ∪ (B – A) ∪ (A∩B) = 1∪2∪3 = (A∪B)
Correct Answer: A
Question 1 Explanation:
(A – B) ∪ (B – A) ∪ (A∩B)

(A – B) = 1
(B – A) = 2
(A∩B) = 3
A∪B = (1∪2∪3)

(A – B) = 1
(B – A) = 2
(A∩B) = 3
A∪B = (1∪2∪3)
(A – B) ∪ (B – A) ∪ (A∩B) = 1∪2∪3 = (A∪B)
Subscribe
Login
0 Comments
