Propositional-Logic
August 15, 2024Engineering-Mathematics
August 15, 2024Probability-and-statistics
| Question 2 |
Consider the two statements.
S1: There exist random variables X and Y such that
EX-E(X)Y-E(Y)2>Var[X] Var[Y]
S2: For all random variables X and Y,
CovX,Y=E|X-E[X]| |Y-E[Y]|
Which one of the following choices is correct?
S1: There exist random variables X and Y such that
EX-E(X)Y-E(Y)2>Var[X] Var[Y]
S2: For all random variables X and Y,
CovX,Y=E|X-E[X]| |Y-E[Y]|
Which one of the following choices is correct?
| S1is false, but S2is true. | |
| Both S1and S2are true. | |
| S1is true, but S2is false. | |
| Both S1and S2 are false. |
Question 2 Explanation:
Variance(X) = Var[X]= E((X-E(X))^2)
For a dataset with single values, we have variance 0.
EX-E(X)Y-E(Y)2>Var[X] Var[Y]
This leads to inequance of 0>0 which is incorrect.
Its not |x-E(x)|. Thus S2 is also incorrect.
For a dataset with single values, we have variance 0.
EX-E(X)Y-E(Y)2>Var[X] Var[Y]
This leads to inequance of 0>0 which is incorrect.
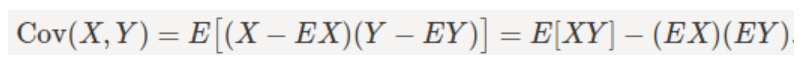
Its not |x-E(x)|. Thus S2 is also incorrect.
Correct Answer: D
Question 2 Explanation:
Variance(X) = Var[X]= E((X-E(X))^2)
For a dataset with single values, we have variance 0.
EX-E(X)Y-E(Y)2>Var[X] Var[Y]
This leads to inequance of 0>0 which is incorrect.
Its not |x-E(x)|. Thus S2 is also incorrect.
For a dataset with single values, we have variance 0.
EX-E(X)Y-E(Y)2>Var[X] Var[Y]
This leads to inequance of 0>0 which is incorrect.
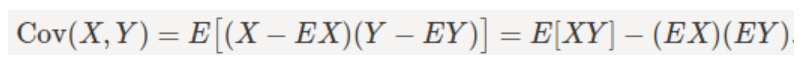
Its not |x-E(x)|. Thus S2 is also incorrect.
Subscribe
Login
0 Comments