Probability-and-statistics
Question 1 |
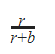 | |
 | |
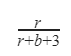 | |
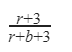 | |

-
There are 8 ways to get ‘red’ in the fourth attempt of drawing
i.e., _ _ _ R these three gaps can be filled with B/R in 222=8 ways
The probability for case (1),


Question 2 |
- If the first question is answered wrong, the student gets zero marks.
- If the first question is answered correctly and the second question is not answered correctly, the student gets the marks only for the first question.
- If both the questions are answered correctly, the student gets the sum of the marks of the two questions.
| question | Probability of answering correctly | marks |
| QuesA QuesB | 0.8 0.5 | 10 20 |
First QuesB and then QuesA. Expected marks 22. | |
First QuesA and then QuesB. Expected marks 16. | |
First QuesA and then QuesB. Expected marks 14. | |
First QuesB and then QuesA. Expected marks 14. |
There are two ways to get marks.
1. Answering first question correctly, and second one wrongly
2. Answering first question and second question correctly.
There are two ways to answer the question paper. First A or First B.
In total we get 4 ways of answering the paper to get marks.
Note: Answering each question is independent, thus P(x intersection y) = P(x)*P(y)|
P(Answering A correctly) =0.8, P( Answering A wrongly) = 1-0.8=0.2
P(Answering B correctly) =0.5, P( Answering B wrongly) = 1-0.5=0.5
|
Probability of Getting marks |
Marks |
|
|
First A correctly, B wrongly |
P(A correctly)*P(B wrongly) |
10+0 = 10 |
|
First A correctly B correctly |
P(A correctly)*P(B Correctly) |
10+20 = 30 |
|
First B correctly, A wrongly |
P(B correctly)*P(A wrongly) |
20+0=20 |
|
First B correctly then A correctly |
P(B correctly)*P(A Correctly) |
20+10=30 |
Expectation formula
E(X)=∑X*P(X)
Expectation for the order:A followed by B = 0.4*10 +0.4*30 = 16
Expectation for the order B followed by A = 0.1*20 + 0.4*30 = 14
As the target is to get maximum marks, the order A followed by B is the correct option
Question 3 |
15.49 |

Question 4 |
(a) Two friends agree to meet at a park with the following conditions. Each will reach the park between 4:00 p.m. and 5:00 p.m. and will see if the other has already arrived. If not, they will wait for 10 minutes or the end of the hour whichever is earlier and leave. What is the probability that the two will not meet?
(b) Given a regular expression for the set of binary strings where every 0 is immediately followed by exactly k 1's and preceded by atleast k 1's (k is a fixed integer).
Theory Explanation. |
Question 5 |
7 |
As no other condition is given,
We need to consider that distinct distribution will be based on the count of balls.
6 identical balls into 3 identical bins.
That can be done in the combination of
[6,0,0], [5,1,0], [ 4,2,0], [3,3,0], [4,1,1],[3,2,1],[2,2,2]
I.e. in 7 ways
Question 6 |
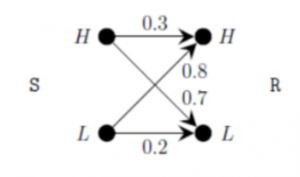
If the received signal is H, the probability that the transmitted signal was H (rounded to 2 decimal places) is _______
0.04 |
Bayes theorem:
Probability of event A happening given that event B has already happened is
P(A/B) = P(B/A)*P(A) / P(B)
Here, it is asked that P( H transmitted / H received).
S can send signal to H with 0.1 probability, S can send signal to L with 0.9 probability.
The complete diagram can be
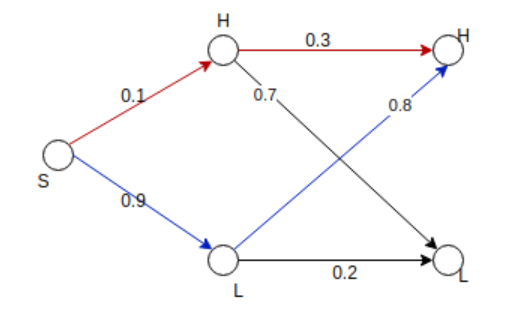
Probability that H Transmitted (H_t) given that H received (H_r)is
P( H_t / H_r) = P( H_r/ H_t) * P(H_t) / P(H_r)
P(H-r) = probability that H received = P( H received from H)+ P(H received from L)
It can be observed from the graph that H can receive in two ways (S to H to H) and (S to L to H)
The P(H_r) = 0.1*0.3 + 0.9*0.8= 0.03+0.72 = 0.75
P(H_received given that H_transmitted) =0.3
P(H transmitted ) = 0.1 i.e.
P( H_t / H_r) = P( H_r/ H_t) * P(H_t) / P(H_r)
= 0.3*0.1 / 0.75 = 0.04
Question 7 |
S1: There exist random variables X and Y such that
EX-E(X)Y-E(Y)2>Var[X] Var[Y]
S2: For all random variables X and Y,
CovX,Y=E|X-E[X]| |Y-E[Y]|
Which one of the following choices is correct?
S1is false, but S2is true. | |
Both S1and S2are true. | |
S1is true, but S2is false. | |
Both S1and S2 are false. |
For a dataset with single values, we have variance 0. EX-E(X)Y-E(Y)2>Var[X] Var[Y]
This leads to inequance of 0>0 which is incorrect.
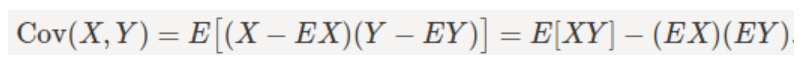
Its not |x-E(x)|. Thus S2 is also incorrect.
Question 8 |
0.37 |

Question 9 |
- All members of A appear in the permutation before any of the members of B.
- All members of B appear in the permutation before any of the members of A.
How many permutations of U separate A from B?
A | |
B | |
C | |
D |
Question 10 |
A and B are independent. | |
A and C are independent. | |
B and C are independent. | |
Prob(B|C) = Prob(B) |
Question 11 |
Consider a finite sequence of random values X = [x1, x2, …, xn]. Let μx be the mean and σx be the standard deviation of X. Let another finite sequence Y of equal length be derived from this as yi = a * xi + b, where a and b are positive constants. Let μy be the mean and σy be the standard deviation of this sequence. Which one of the following statements is INCORRECT?
Index position of mode of X in X is the same as the index position of mode of Y in Y. | |
Index position of median of X in X is the same as the index position of median of Y in Y. | |
μy = aμx + b | |
σy = aσx + b |
(σy)2 is variance so,
yi = a * xi + b
(σy)2 = a2 (σx)2
⇒ σy = a σx
Hence option (D) is incorrect.
Question 12 |
2.5 | |
3 | |
3.5 | |
4 | |
None of the above |
Question 13 |


a | |
b | |
c | |
d | |
e |
Question 14 |
17 / 2401
| |
48 / 2401
| |
105 / 2401 | |
175 / 2401 | |
294 / 2401 |
Question 15 |
P(A) > P(B) | |
P(A) = 1/27 | |
P(A) > P(A|B) | |
P(A) < P(A|B) | |
None of the above |
Question 16 |
Hint: what is the probability that the i-th ball is drawn at the i-th draw? Now can you use linearity of expectation to solve the problem?
1 | |
1.5 | |
2 | |
2.5 | |
None of the above |
Question 17 |

a | |
b | |
c | |
d | |
e |
Question 18 |
1/4 | |
1/3 | |
1/2 | |
2/7 | |
2/5 |
Question 19 |
E[(U1 + U2)| max(U1, U2) ≥ 0.5]
equals
7/6 | |
8/7 | |
6/7 | |
1.1 | |
None of the above |
Question 20 |
Hint: (exp(x) + exp(y))/2 ≥ exp((x + y)/2).
E[X] < ln 2 | |
E[X] > ln 2 | |
E[X] ≥ ln 2 | |
E[X] ≤ ln 2 | |
None of the above |
Question 21 |
R2 is uniformly distributed in [0, 1] | |
πR2 is uniformly distributed in [0, 1] | |
π R2 is uniformly distributed in [0, 1] | |
2πR2 is uniformly distributed in [0, 1] | |
None of the above |
Question 22 |
R=1/(p+q-2pq) | |
R=1/(p+q-p2q | |
R is independent of p and q | |
R=1/(1+2pq-p-q) | |
None of the above |
Question 23 |

20.22 | |
19.47 | |
21.12 | |
20.14 |
Question 24 |
1/3 | |
3/4 | |
8/9 | |
4/9 |
Question 25 |
0.47 | |
0.40 | |
0.74 | |
0.64 | |
None of the above |
Question 26 |
a | |
b | |
c | |
d |
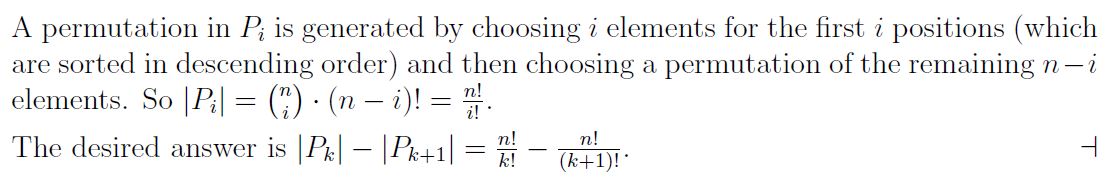
Question 27 |
1/12 | |
1/6 | |
2/9 | |
2/7 |

Question 28 |
Let
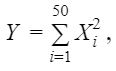
and E(Y) = a and Var(Y) = b. Then, the ordered pair (a, b) is :
(50, 100) | |
(50, 50) | |
(25, 50) | |
(25, 100) |
Question 29 |
(Ignore leap years, so there are only 365 possible birthdays. Assume that birthdays fall with equal probability on each of the 365 days of the year.)
23 | |
28 | |
92 | |
183 | |
366 |
Question 30 |
p = 0 | |
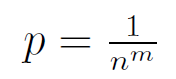 | |
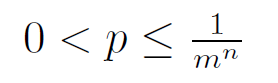 | |
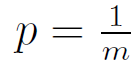 | |
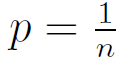 |
Question 31 |
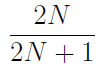 | |
 | |
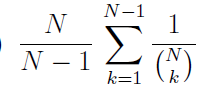 | |
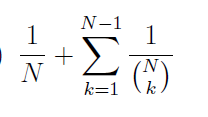 | |
None of the above |
