HCU PHD CS MAY 2010
Question 1 |
The average case time complexity of finding minimum element in a Max-heap having N elements is
Θ(N) | |
Θ(logN) | |
O(1) | |
Θ(NlogN) |
Question 1 Explanation:
In max-heap to find the minimum element we have to search the all leaf nodes,because the smallest element in max heap will be present at the leaves.And the no. of leaf nodes in heap tree is approx n/2.Hence average time complexity required to find the minimum element in max-heap is Θ(N).
Question 2 |
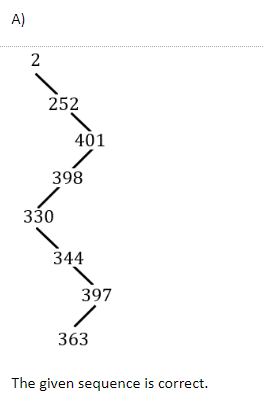
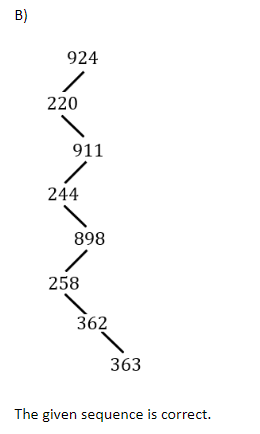
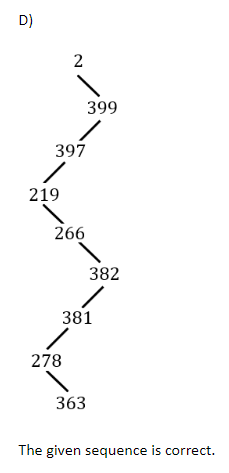
The integers {1-1000} are stored in a Binary search tree (BST). Suppose the search algorithm is implemented on the key 363, one of the following sequences is NOT a possible sequence of nodes that is examined. It is
2, 252,401, 398, 330, 344, 397, 363 | |
924, 220, 911, 244,898, 258, 362, 363 | |
925, 202, 911,240, 912, 345,245, 363 | |
2, 399, 397, 219, 266, 382, 381, 278, 363 |
Question 2 Explanation:

Question 3 |
It is NOT KNOWN if an NP-complete problem A is such that
A Ɛ NP | |
A Ɛ P | |
A Ɛ NP-Hard | |
Circuit-Sat reducible to A. |
Question 4 |
Which of the following statements is TRUE about the worst-case time complexity for operations on heaps?
Neither insertion nor removal is better than linear. | |
Insertion is better than linear, but removal is not. | |
Removal is better than linear, but insertion is not. | |
Both insertion and removal are better than linear |
Question 4 Explanation:
Both insertion and removal of elements in heap take O(logn) time which is better than linear which is O(n) time.
Question 5 |
A priority queue is implemented by storing the items in a min heap(using an array for the heap items). In a min-heap, the value at parent is less than the value at the child position. If re-heapification is done upward and the out-of-place node is at data[i] with priority given by data[i], Which of the following boolean expressions is TRUE to indicate that the re-heapification IS NOT YET DONE.
(i > 0) | |
(data[(i, - 1)/ 2] < data[i]) | |
(i > 0) && (datal(i-1)/2] < data[i]) | |
(i > 0) ll (data[(i -1)/2) < data[i]) |
Question 6 |
An algorithm has a run time complexity of o(log N). The algorithm requires 110 operations for an input of size 1000. When the input size is doubled to 2000, the algorithm now requires 120 operations. What is your best gUess for the number of operations required when the size is doubled to 4000?
130 | |
140 | |
150 | |
160 |
Question 6 Explanation:
We can use the theoretical concept here. Initially when the input size was 1000 the no. of operations required was 110.Now when input size is doubled to 2000, the no. of operations got increased by 10 and became 120. Now again the input size is further doubled to 4000 ,so again the no. of operations will get increased by 10 and the no. of operations will become 130.
Question 7 |
A stack data structure is used in which of the following implementations
Priority queue | |
Depth First Search | |
Breadth First Search | |
Post order traversal |
Question 7 Explanation:
Priority queue uses heap data structure.
Depth first search uses stack data structure.
Breadth first search uses Queue data structure.
Post order traversal uses tree data structure.
Depth first search uses stack data structure.
Breadth first search uses Queue data structure.
Post order traversal uses tree data structure.
Question 8 |
Class of languages recognized by finite automata is called as:
Context Sensitive languages | |
Recursive Language | |
Regular Language | |
Context free languages |
Question 8 Explanation:
Class of languages recognized by finite automata is called regular language.
Question 9 |
Given an arbitrary Non-deterministic Finite Automaton (NFA) with N states, the maximum number of states in an equivalent minimized deterministic Finite Automaton (DFA) is at least.
N2 | |
2N | |
2N | |
N! |
Question 9 Explanation:
The question is wrong .The question should have asked ”the maximum number of states in an equivalent minimized deterministic Finite Automaton (DFA) is at most”.
In DFA any subset of N states can become a new state in DFA and can remain even if the DFA is minimized. No. of subsets possible with N is 2^N.So at max we can have 2^N state in the minimized DFA.
In DFA any subset of N states can become a new state in DFA and can remain even if the DFA is minimized. No. of subsets possible with N is 2^N.So at max we can have 2^N state in the minimized DFA.
Question 10 |
Which of the following statements is FALSE?
If a language is context free it can always be accepted by a non-deterministic push-down automaton | |
The union of two context free languages is context free | |
The intersection of two context free languages is context free | |
A regular language is context free |
Question 10 Explanation:
Option C is false because context free language is not closed under intersection.
Question 11 |
If the regular set A is represented by A = (01 + 1)* and the regular set B is represented by B =((01)*1*)*, which of the following statements is TRUE?
A is a proper subset of B | |
B is a proper subset of A | |
A and B are incomparable | |
A= B. |
Question 11 Explanation:
Note that,
(a+b)* = (a*+b*)*= (a+b*)* = (a*+b)* = (a*b*)*
So from above Note it is clear that ,
(01+1)* = ((01)*1*)*
(a+b)* = (a*+b*)*= (a+b*)* = (a*+b)* = (a*b*)*
So from above Note it is clear that ,
(01+1)* = ((01)*1*)*
Question 12 |
The Language L={a2k : k ≥ 0} is
Regular Language | |
Non-regular Language | |
Non Context-free language | |
None of the above |
Question 12 Explanation:

There are 12 questions to complete.
