HCU PHD CS MAY 2017
Question 1 |
Two motorists set out at the same time from A to B, a distance of 100 miles. They both followed the same route and travelled at different though uniform speeds of integral number of miles /hour. The difference in their speeds was a prime number of miles/hour. After they had been driving for 2 hrs, the distance of the slower car from A was five times that of the faster car from B. How fast did the motorists drive?
30 and 37 miles/hour | |
40 and 42 miles/hour | |
47 and 49 miles/hour | |
None of the above |
Question 1 Explanation:
The two motorists:
Let d=the distance the faster car has traveled. Then it still has 100-d miles to go, and the slow car has, therefore, gone 500-5d miles. Let A and B be the rates of the fast and slow cars in mph. Then d/A = (500-5d)/B = 2
We get B=250-5B
Then A-B=6f-250
=(3A-125).
But since A-B is prime 3A-125=1
hence A=42mph and B=40 mph
Let d=the distance the faster car has traveled. Then it still has 100-d miles to go, and the slow car has, therefore, gone 500-5d miles. Let A and B be the rates of the fast and slow cars in mph. Then d/A = (500-5d)/B = 2
We get B=250-5B
Then A-B=6f-250
=(3A-125).
But since A-B is prime 3A-125=1
hence A=42mph and B=40 mph
Question 2 |
A job is done by M men in D days. Then M + N men can do the same job in
(MD)/M+N days | |
D/M((M +N) days | |
D-(D/M)*N days | |
D-(M/D)*N days |
Question 2 Explanation:
let's assume 1 man will take m time to do the same job, so rate of working for i man is: 1(job)/d*m(days)= 1/d*m
More man means job will done faster so the new rate will be: (m+n)*(rate of 1 man) = m+n/d*m
Now convert this to m+r men by dividing top and bottom will take d*m/m+n
More man means job will done faster so the new rate will be: (m+n)*(rate of 1 man) = m+n/d*m
Now convert this to m+r men by dividing top and bottom will take d*m/m+n
Question 3 |
An academic institute starts a class at 10:00 A.M. and ends at 1:47 P.M. It has 4
periods of equal distribution of time. After each period there is a gap of 5 minutes to
start another period. What is the exact duration of the period?
51 | |
52 | |
53 | |
57 |
Question 3 Explanation:
let’s count total academic minutes in a day from 10:00 am to 1:47 pm i.e 227 minutes.
Total period is =4
Time gap after each period is = 5 minutes. First class starts at 10:00 am so total gap will be 5*3=15 minutes. Deduct gap from total academic minutes = 227- 15=212
Total 4 periods we have given in the question so, 212/4= 53 minutes.
Total period is =4
Time gap after each period is = 5 minutes. First class starts at 10:00 am so total gap will be 5*3=15 minutes. Deduct gap from total academic minutes = 227- 15=212
Total 4 periods we have given in the question so, 212/4= 53 minutes.
Question 4 |
A contractor estimated that one of his bricklayers would take 9 hrs to build a certain
wall and the other 10 hours. However, he knew from experience that when they worked
together, 10 fewer bricks laid per hour. Since he was in a hurry, he put both men
on the job and found it took exactly 5 hours to build the wall. How many bricks did
it contain?
18 | |
90 | |
900 | |
It can not be determined from the given data |
Question 5 |
The number of ways in which 3 men and 2 women can sit in a row so that no two men
are adjacent is
12 | |
24 | |
72 | |
19 |
Question 5 Explanation:
The only possibility is
M W M W M
Where M represents men and W represents women.
Now three men can be arranged among themselves in 3! Ways and two women can be arranged in 2! ways.Hence the answer is 3! * 2! =12
M W M W M
Where M represents men and W represents women.
Now three men can be arranged among themselves in 3! Ways and two women can be arranged in 2! ways.Hence the answer is 3! * 2! =12
Question 6 |
Given the statement, "I always cut the top-right corner of a milk packet for opening it", a milk packet with its top-right corner cut is
a necessary condition for the packet to have been opened by me | |
a sufficient condition for the packet to have been opened by me | |
both Ii necessary and a sufficient condition for the packet to have been opened by
me
| |
sometimes a necessary condition and sometimes a sufficient condition for the
packet to have been opened by me
|
Question 6 Explanation:
The given statement is necessary condition that the packet was opened by me but it is not sufficient condition, because some other person also might open the milk packet in same way. But if it was opened by me then it has to be cut from top right corner ,hence nessecary condition.
Question 7 |
A common problem in Computer Science research is to minimise an equation of the Form
where λ is a parameter, Et , Em and Ed are the total, model and data errors. Model
error reflects the mismatch between predicted and actual values, while data error is
the error due to noise in the data. For noisy data, the value of λ should be
Close to 0 | |
Close to 1 | |
Close to 0.5 | |
None of the above |
Question 8 |
Using general knowledge about Computer Science and by reading the following paragraph carefully, answer the Questions 8 - 12 below:
Princeton asked me to develop a course in automata theory. Since there were no courses or books on the subject, I asked McCluskey to recommend some materials for a course on automata theory. He gave me a list of six papers and told me that the material would probably give students a good background in automata theory. McCluskey'S list included works by Warren McCulloch and Walter Pitts, Michael Rabin and Dana Scott, John Backus and Peter Naur, Noam Chomsky, Juris Hartmanis and RichardStearns, and, of course, Alan Turing.
In 1943 McCulloch and Pitts, working in neurophysiology, published a paper on a logical calculus for describing events in neuron nets. The paper had a notation for describing how these strings of zeros and ones combine in neurons to produce new strings of zeros and ones. This notation was subsequently developed into the language of regular expressions for describing sets of strings. Rabin and Scott were mathematicians who developed a model of a computer with a finite amount of memory. They called this model the finite-state automaton, and showed that the possible behaviors of finite-state automata were precisely those behaviors that could be described by the regular expressions that grew out of the work of McCulloch and Pitts. ...... The work of Hartmanis and Stearns attracted researchers and focused· attention on the topic of complexity. Among the more significant advances that resulted were the classification of the complexity of most major mathematical theories, the reducibility of many combinatorial problems, the concept of NP-completeness, and a deeper understanding of concepts such as randomness. Also, through this course I met Jeffrey Ullman and Alfred Aho, with whom I subsequently collaborated for many years. Formal Languages and Automata Theory, which I wrote with Ullman, also evolved from this course.
Who is the ’I’, in the passage?
McCluskey· | |
Jeffrey Ullman | |
John Hopcroft | |
Edsger Dijkstra |
Question 9 |
Using general knowledge about Computer Science and by reading the following paragraph carefully, answer the Questions 8 - 12 below:
Princeton asked me to develop a course in automata theory. Since there were no courses or books on the subject, I asked McCluskey to recommend some materials for a course on automata theory. He gave me a list of six papers and told me that the material would probably give students a good background in automata theory. McCluskey'S list included works by Warren McCulloch and Walter Pitts, Michael Rabin and Dana Scott, John Backus and Peter Naur, Noam Chomsky, Juris Hartmanis and RichardStearns, and, of course, Alan Turing.
In 1943 McCulloch and Pitts, working in neurophysiology, published a paper on a logical calculus for describing events in neuron nets. The paper had a notation for describing how these strings of zeros and ones combine in neurons to produce new strings of zeros and ones. This notation was subsequently developed into the language of regular expressions for describing sets of strings. Rabin and Scott were mathematicians who developed a model of a computer with a finite amount of memory. They called this model the finite-state automaton, and showed that the possible behaviors of finite-state automata were precisely those behaviors that could be described by the regular expressions that grew out of the work of McCulloch and Pitts. ...... The work of Hartmanis and Stearns attracted researchers and focused· attention on the topic of complexity. Among the more significant advances that resulted were the classification of the complexity of most major mathematical theories, the reducibility of many combinatorial problems, the concept of NP-completeness, and a deeper understanding of concepts such as randomness. Also, through this course I met Jeffrey Ullman and Alfred Aho, with whom I subsequently collaborated for many years. Formal Languages and Automata Theory, which I wrote with Ullman, also evolved from this course. ...... denotes some missing sentences in the passage. What are the most likely missing sentences?
Sentences about Hopcroft's early work in the course | |
Sentences about work by Hartmanis and Stearns | |
Sentences about work by Backus, Naur and Chomsky | |
Sentences about Princeton university |
Question 9 Explanation:
The missing sentences was about Backus naur and Chomsky because the second paragraph contains all the names of the McCluskey'S list except these two names.
Question 10 |
Using general knowledge about Computer Science and by reading the following paragraph carefully, answer the Questions 8 - 12 below:
Princeton asked me to develop a course in automata theory. Since there were no courses or books on the subject, I asked McCluskey to recommend some materials for a course on automata theory. He gave me a list of six papers and told me that the material would probably give students a good background in automata theory. McCluskey'S list included works by Warren McCulloch and Walter Pitts, Michael Rabin and Dana Scott, John Backus and Peter Naur, Noam Chomsky, Juris Hartmanis and RichardStearns, and, of course, Alan Turing.
In 1943 McCulloch and Pitts, working in neurophysiology, published a paper on a logical calculus for describing events in neuron nets. The paper had a notation for describing how these strings of zeros and ones combine in neurons to produce new strings of zeros and ones. This notation was subsequently developed into the language of regular expressions for describing sets of strings. Rabin and Scott were mathematicians who developed a model of a computer with a finite amount of memory. They called this model the finite-state automaton, and showed that the possible behaviors of finite-state automata were precisely those behaviors that could be described by the regular expressions that grew out of the work of McCulloch and Pitts. ...... The work of Hartmanis and Stearns attracted researchers and focused· attention on the topic of complexity. Among the more significant advances that resulted were the classification of the complexity of most major mathematical theories, the reducibility of many combinatorial problems, the concept of NP-completeness, and a deeper understanding of concepts such as randomness. Also, through this course I met Jeffrey Ullman and Alfred Aho, with whom I subsequently collaborated for many years. Formal Languages and Automata Theory, which I wrote with Ullman, also evolved from this course.
Who invented the finite state automaton?
Hopcroft and Ullman | |
Chomsky | |
McCulloch and Pitts | |
Rabin and Scott |
Question 10 Explanation:
From the line “Rabin and Scott were mathematicians who developed a model
of a computer with a finite amount of memory. They called this model the finite-state
Automaton” it is clear that the answer is Rabin and Scott.
Question 11 |
Using general knowledge about Computer Science and by reading the following paragraph carefully, answer the Questions 8 - 12 below:
Princeton asked me to develop a course in automata theory. Since there were no courses or books on the subject, I asked McCluskey to recommend some materials for a course on automata theory. He gave me a list of six papers and told me that the material would probably give students a good background in automata theory. McCluskey'S list included works by Warren McCulloch and Walter Pitts, Michael Rabin and Dana Scott, John Backus and Peter Naur, Noam Chomsky, Juris Hartmanis and RichardStearns, and, of course, Alan Turing.
In 1943 McCulloch and Pitts, working in neurophysiology, published a paper on a logical calculus for describing events in neuron nets. The paper had a notation for describing how these strings of zeros and ones combine in neurons to produce new strings of zeros and ones. This notation was subsequently developed into the language of regular expressions for describing sets of strings. Rabin and Scott were mathematicians who developed a model of a computer with a finite amount of memory. They called this model the finite-state automaton, and showed that the possible behaviors of finite-state automata were precisely those behaviors that could be described by the regular expressions that grew out of the work of McCulloch and Pitts. ...... The work of Hartmanis and Stearns attracted researchers and focused· attention on the topic of complexity. Among the more significant advances that resulted were the classification of the complexity of most major mathematical theories, the reducibility of many combinatorial problems, the concept of NP-completeness, and a deeper understanding of concepts such as randomness. Also, through this course I met Jeffrey Ullman and Alfred Aho, with whom I subsequently collaborated for many years. Formal Languages and Automata Theory, which I wrote with Ullman, also evolved from this course.
What was the difficulty in offering the course on Finite Automata Theory at Princeton?
There were no textbooks for the subject | |
There were no teachers for the subject | |
There were no students for the subject | |
None of the above |
Question 11 Explanation:
From the line”Since there were no courses or books on the subject” it is clear that the answer is option A.
Question 12 |
Using general knowledge about Computer Science and by reading the following paragraph carefully, answer the Questions 8 - 12 below:
Princeton asked me to develop a course in automata theory. Since there were no courses or books on the subject, I asked McCluskey to recommend some materials for a course on automata theory. He gave me a list of six papers and told me that the material would probably give students a good background in automata theory. McCluskey'S list included works by Warren McCulloch and Walter Pitts, Michael Rabin and Dana Scott, John Backus and Peter Naur, Noam Chomsky, Juris Hartmanis and RichardStearns, and, of course, Alan Turing.
In 1943 McCulloch and Pitts, working in neurophysiology, published a paper on a logical calculus for describing events in neuron nets. The paper had a notation for describing how these strings of zeros and ones combine in neurons to produce new strings of zeros and ones. This notation was subsequently developed into the language of regular expressions for describing sets of strings. Rabin and Scott were mathematicians who developed a model of a computer with a finite amount of memory. They called this model the finite-state automaton, and showed that the possible behaviors of finite-state automata were precisely those behaviors that could be described by the regular expressions that grew out of the work of McCulloch and Pitts. ...... The work of Hartmanis and Stearns attracted researchers and focused· attention on the topic of complexity. Among the more significant advances that resulted were the classification of the complexity of most major mathematical theories, the reducibility of many combinatorial problems, the concept of NP-completeness, and a deeper understanding of concepts such as randomness. Also, through this course I met Jeffrey Ullman and Alfred Aho, with whom I subsequently collaborated for many years. Formal Languages and Automata Theory, which I wrote with Ullman, also evolved from this course.
Which of the following did not grow out of the work by Hartmanis and Stearns?
Regular expressions | |
Reducibility of combinatorial problems | |
Classification of complexity | |
NP-Completeness |
Question 12 Explanation:
From the line “The work of Hartmanis and Stearns attracted researchers
and focused· attention on the topic of complexity. Among the more significant advances
that resulted were the classification of the complexity of most major mathematical theories,
the reducibility of many combinatorial problems, the concept of NP-completeness, and a
deeper understanding of concepts such as randomness” it is clear that regular expression was not grown out of the work by Hartmanis and Stearns.
Question 13 |
Which plots show the relationship between two or three variables when comparing data
sets consisting of multiple observations?
Histograms | |
Scatter Plots | |
Probability Plots | |
All the above |
Question 14 |
Variability in groups of observations with widely differing means can be compared
using the following measure
Coefficient of variation | |
Mean deviation
| |
Measure of skewness | |
None of the above |
Question 15 |
Features / attributes of patterns, which can be measured, are called
Qualitative measure | |
Data | |
Variables | |
All |
Question 16 |
Find the sample variance, standard deviation and range of the following data: 572, 572, 573, 568, 569, 575, 565, 570
Variance =10, standard deviation = 3.162, range = 11 | |
Variance =13, standard deviation = 4.162, range = 10 | |
Variance =10, standard deviation = 3.162, range = 09 | |
Variance =10, standard deviation = 3.162, range = 10 |
Question 17 |
The president and treasurer are to be chosen from a student club consisting of 50
people. How many different choices of officers are possible if there are no restrictions?
2450 | |
2500 | |
1225 | |
1250 |
Question 17 Explanation:
We are picking 2 out of a field of 50, and order does matter.So
answer is P(50,2) = 2450
answer is P(50,2) = 2450
Question 18 |
In a college football training session, the defensive coordinator needs to have 10 players
standing in a row. Among these 10 players, there are 1 freshman, 2 sophomore, 4 juniors
and 3 seniors. How many different ways can they be arranged in a row if only their
class level will be distinguished?
14600 | |
12600 | |
12800 | |
None of the above
|
Question 18 Explanation:
Since only their class level will be distinguished. So 2 sophomore will be treated same, 4 juniors will be treated same, and 3 seniors will be treated same.
Hence the no. of ways they can be arranged in a row,
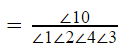
=12600
Hence the no. of ways they can be arranged in a row,
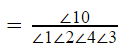
=12600
Question 19 |
In how many ways can 5 different trees be planted in a circle?
24 | |
12 | |
6 | |
120 |
Question 19 Explanation:
There are a total of 5! (=120) ways to plant five different trees. However, the trees are in a circle, in which each "way" is counted five times, due to rotations. This leaves us 5!/5 = 4! = 24 ways to plant five different trees in a circle.
There are 19 questions to complete.
