aptitude
Question 1 |
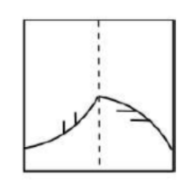
A transparent square sheet shown above is folded along the dotted line. The folded sheet will look like _______.
A | 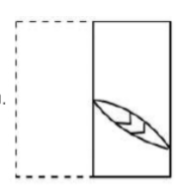 |
B |  |
C | 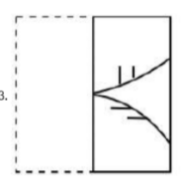 |
D | 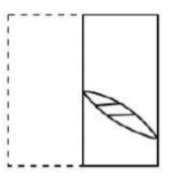 |
Question 2 |
A | as worse as |
B | as well as |
C | as better as |
D | as nicest as |
Question 3 |
A | Vegetables |
B | Sharp |
C | Blunt |
D | Cut |
Question 4 |
A | 66 |
B | 22 |
C | 88 |
D | 110 |
Given Initial ratio : 3:13:6
Total number of students initially = 3x+13x+6x = 22x
From the given question, we can write 3x+18 = 15y -----I
13x+18 = 35y-----II
6x+18 = 21y------III
I - II => -10X = -20Y
X=2Y------IV
Put IV in III => 6(2y) + 18 = 21y
12y + 18 = 21y
9y = 18
y = 2 -----V
Substitute V in I => 3x + 18 = 30
3x = 12
x = 4
Number of initial students = 22x = 22(4) = 88
Question 5 |
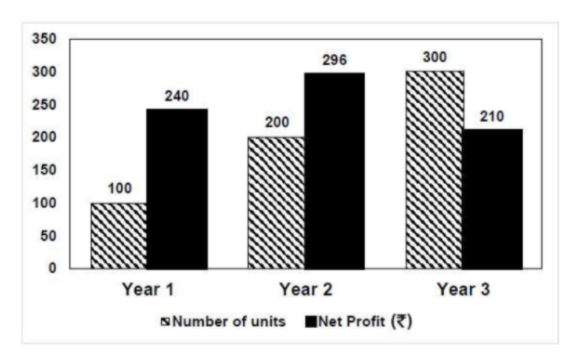
The number of units of a product sold in three different years and the respective net profits are presented in the figure above. The cost/unit in Year 3 was ₹ 1, which was half the cost/unit in Year 2. The cost/unit in Year 3 was one-third of the cost/unit in Year 1. Taxes were paid on the selling price at 10%, 13% and 15% respectively for the three years. Net profit is calculated as the difference between the selling price and the sum of cost and taxes paid in that year.
The ratio of the selling price in Year 2 to the selling price in Year 3 is ______.
A | 1:1 |
B | 3:4 |
C | 1:2 |
D | 4:3 |
According to the given data:
Year Cost/unit Number of units Cost Price
1 ₹ 3 100 300
2 ₹ 2 200 400
3 ₹ 1 300 300
Cost Price = Cost/unit x Number of units
Net Profit = Selling Price - (Cost Price + (Tax% x selling price )
Year 2:
296 = SP - (400 + (13/100) x SP)
=>296 = 0.87SP - 400
=> 0.87SP = 696
=> SP = ₹ 800
Year 3:
210 = SP - (300 + (15/100) x SP)
=> 210 = 0.85SP - 300
=> 0.85SP = 510
=> SP = ₹ 600
The ratio of selling price in Year 2 to the selling price in year 3 = 800:600
= 4:3
Question 6 |
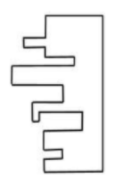
A jigsaw puzzle has 2 pieces. One of the pieces is shown above. Which one of the given options for the missing piece when assembled will form a rectangle? The piece can be moved, rotated or flipped to assemble with the above piece.
A |  |
B | 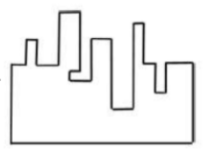 |
C | 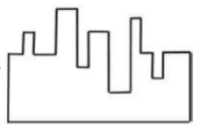 |
D | 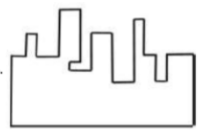 |
Question 7 |
A | 2 |
B | 4 |
C | 8 |
D | 6 |
Expand the given equation:
x2+1/4 - x -x2 -9/4 +3x = x+2
=> -2 + 2x = x + 2
X = 4
Question 8 |
A | 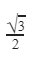 |
B |  |
C | 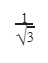 |
D | 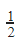 |
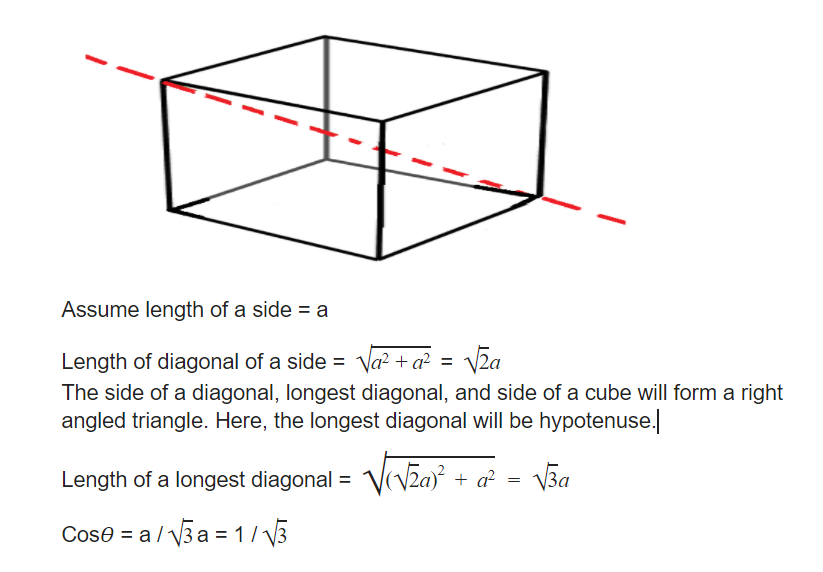
Question 9 |
Observation I: S is taller than R.
Observation II: Q is the shortest of all.
Observation III: U is taller than only one student.
Observation IV: T is taller than S but is not the tallest.
The number of students that are taller than R is the same as the number of students shorter than _______.
A | S |
B | P |
C | T |
D | R |
Number of students taller than R = Number of students shorter than S = 3
Question 10 |
Two straight lines are drawn perpendicular to each other in X-Y plane. If α and β are the acute angles the straight lines make with the X-axis, then α+β is ______.
A | 60° |
B | 120° |
C | 180° |
D | 90° |
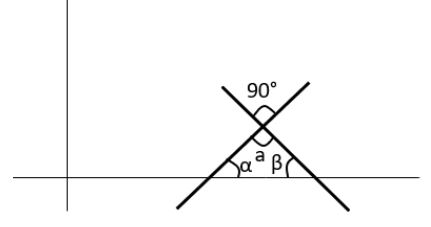
We know a + α + β = 180
α + β = 180 - 90
α + β = 90
Question 11 |
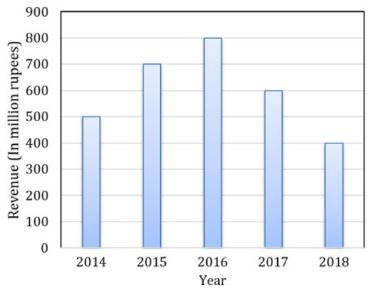
The total revenue of a company during 2014-2018 is shown in the bar graph. If the total expenditure of the company in each year is 500 million rupees, then the aggregate profit or loss (in percentage) on the total expenditure of the company during 2014-2018 is ______.
A | 20% profit |
B | 20% loss |
C | 16.67% loss |
D | 16.67% profit |
2014-2018
Total expenditure = 500 million/year = 500 × 5 = 2500 million
Revenue total (from the graph)
= 400 + 500 + 600 + 700 + 800
= 3000 million
Profit = 3000 - 2500 = 500
⟹ 500/2500 = 20% profit
Question 12 |
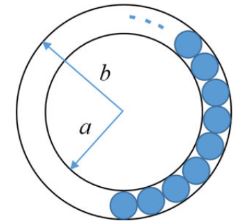
The figure below shows an annular ring with outer and inner radii as b and a, respectively. The annular space has been painted in the form of blue colour circles touching the outer and inner periphery of annular space. If maximum n number of circles can be painted, then the unpainted area available in annular space is ______.
A | π[(b2 - a2) + π/4(b - a)2] |
B | π[(b2 - a2) - π/4(b - a)2] |
C | π[(b2 - a2) - n(b - a)2] |
D | π[(b2 - a2) + n(b - a)2] |
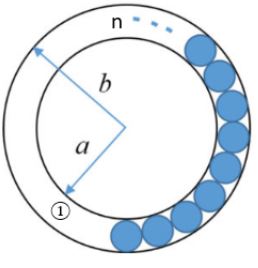
Area of non-painted between 2 circles area of part 1 = πb2 - πa2 = π(b2 - a2)
Radius of painted circles = b-a/2
Area of painted circle = π(b-a/2)2
For n circles = nπ(b-a/2)2
Non-painted area = π[b2 - a2- n/4(b - a)2]
Question 13 |
Goods and Services Tax (GST) is an indirect tax introduced in India in 2017 that is imposed on the supply of goods and services, and it subsumes all indirect taxes except few. It is a destination-based tax imposed on goods and services used, and it is not imposed at the point of origin from where goods come. GST also has a few components specific to state governments, central government and Union Territories (UTs).
Which one of the following statements can be inferred from the given passage?
A | GST includes all indirect taxes.
|
B | GST is imposed at the point of usage of goods and services.
|
C | GST does not have a component specific to UT. |
D | GST is imposed on the production of goods and services.
|
Question 14 |
Select the word that fits the analogy:
Cook : Cook :: Fly : _____
A | Flyer |
B | Flying |
C | Flew |
D | Flighter |
Fly-Flyer
Question 15 |
The drawn of the 21st century witnessed the melting glaciers oscillating between giving too much and too little to billions of people who depend on them for fresh water. The UN climate report estimates that without deep cuts to man-made emissions, at least 30% of the northern hemisphere’s surface permafrost could melt by the end of the century. Given this situation of imminent global exodus of billions of people displaced by rising seas, nation-states need to rethink their carbon footprint for political concerns, if not for environmental ones.
Which one of the following statements can be inferred from the given passage?
A | Nation-states are responsible for providing fresh water to billions of people. |
B | Billions of people are affected by melting glaciers.
|
C | Nation-states do not have environmental concerns. |
D | Billions of people are responsible for man-made emissions. |
Question 16 |
There are multiple routes to reach from node 1 to node 2, as shown in the network.
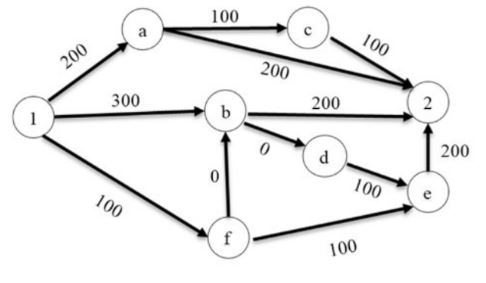
The cost of travel on an edge between two nodes is given in rupees. Nodes ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, and ‘f’ are toll booths. The toll price at toll booths marked ‘a’ and ‘e’ is Rs.200, and is Rs.100 for the other toll booths. Which is the cheapest route from node 1 to node 2?
A | 1-f-e-2
|
B | 1-f-b-2 |
C | 1-b-2 |
D | 1-a-c-2
|
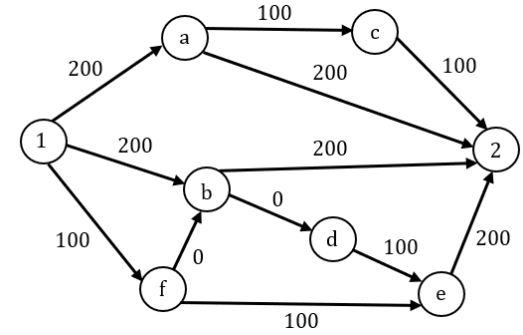
1 - f - e - 2 ─ 100 + 100 + 200 = 400
1 - f - b - 2 ─ 100 + 0 + 200 = 300 ⇾ shortest [Answer]
1 - b - 2 ─ 300 + 200 = 500
1 - a - c ─ 2 - 200 + 100 + 100 = 400
Question 17 |
Raman is confident of speaking English _____ six months as he has been practicing regularly_____the last three weeks.
A | for, in |
B | during, for
|
C | for, since
|
D | within, for
|
Question 18 |
If P = 3, R = 27, T = 243, then Q+S = ______.
A | 80 |
B | 110 |
C | 40 |
D | 90 |
P=31, Q=32, R=33, S=34, T=35
Q+S = 32 + 34 = 9+81 = 90
Question 19 |
His knowledge of the subject was excellent but his classroom performance was ______.
A | good
|
B | praiseworthy |
C | extremely poor |
D | desirable
|
Question 20 |
“From where are they bringing their books? __________ bringing __________ books from __________.”
The words that best fill the blanks in the above sentence are
A | Their, they’re, there |
B | They’re, their, there |
C | There, their, they’re |
D | They’re, there, there |
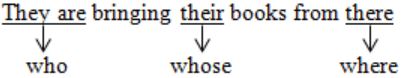
Question 21 |
"A _______ investigation can sometimes yield new facts, but typically organized ones are more successful."
The word that best fills the blank in the above sentence is
A | meandering |
B | timely |
C | consistent |
D | systematic |
Question 22 |
The area of a square is d. What is the area of the circle which has the diagonal of the square as its diameter?
A | πd |
B | πd2 |
C | (1/2)πd2 |
D | (1/2)πd |
Area of a square A = a2 (where a is side)
In the question,
Area of a square = d
The side of a square = √d
Diagonal of a square = Diameter of circle
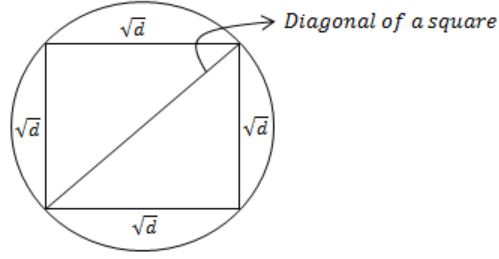
From Pythagoras theorem,
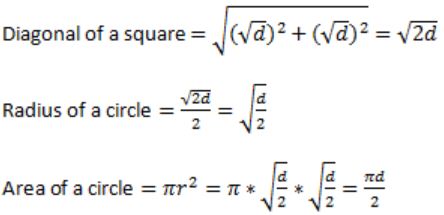
Question 23 |
What is the missing number in the following sequence?
2, 12, 60, 240, 720, 1440, _______, 0A | 2880 |
B | 1440 |
C | 720 |
D | 0 |
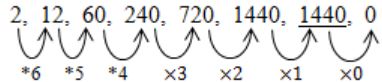
2 × 6 = 12
12 × 5 = 60
60 × 4 = 240
240 × 3 = 720
720 × 2 = 1440
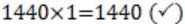
1440 × 0 = 0
Question 24 |
What would be the smallest natural number which when divided either by 20 or by 42 or by 76 leaves a remainder of '7' in each case?
A | 3047 |
B | 6047 |
C | 7987 |
D | 63847 |
Take the LCM of 20, 42, 76 i.e., 7980.
⟹ Remainder = 7
⟹ Smallest number divisible by 20 (or) 42 (or) 72 which leaves remainder 7 is = 7980 + 7 = 7987
Method-II:
Option I:
3047 – 7 = 3040
3040 not divisible by 42
Option II:
6040 not divisible by 42
Option III:
7980 divisible by 20, 42, 76
Option IV:
63840 divisible by 20, 42, 76
→ Smallest (7980, 63840) = 7980
→ 7980 + remainder 7 = 7987
Question 25 |
If pqr ≠ 0 and p -x = 1/q, q -y = 1/r, r -z = 1/p, what is the value of the product xyz?
A | -1 |
B | 1/pqr |
C | 1 |
D | pqr |
→ p-x = 1/q ⟹ 1/px = 1/q
⟹ q = px
⟹ log q = log px
⟹ x log p = log q
⟹ x = log q/ log p
→ q-y = 1/r ⟹ 1/qy = 1/r
⟹ qy = r
⟹ y log q = log r
⟹ y = log r/ log q
→ r-z = 1/p ⟹ 1/rz = 1/p
⟹ p = rz
⟹ log rz = log p
⟹ z log r = log p
⟹ z = log p/ log r
XYZ = log q/ log p * log r/ log q * log p/ log r =1
Question 26 |
In the figure below, ∠DEC + ∠BFC is equal to

A | ∠BCD - ∠BAD |
B | ∠BAD + ∠BCF
|
C | ∠BAD + ∠BCD |
D | ∠CBA + ADC |
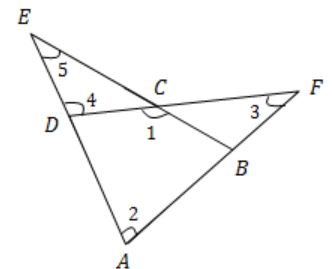
→ ∠1 = ∠5 + ∠4 ………(i)
According to triangular property:
Angle of exterior = sum of interior angles
→ ∠4 = ∠3 + ∠2 ……….(ii)
By substituting (ii) in (i)
→ ∠1 = ∠5 + ∠3 + ∠2
→ ∠1 = ∠BCD
∠2 = ∠BAD
→ ∠BCD - ∠BAD = ∠1 - ∠2
= ∠5 + ∠3 + ∠2 - ∠2
= ∠ 5 + ∠3
= ∠DEC + ∠BFC
Question 27 |
In a party, 60% of the invited guests are male and 40% are female. If 80% of the invited guests attended the party and if all the invited female guests attended, what would be the ratio of males to females among the attendees in the party?
A | 2:3 |
B | 1:1 |
C | 3:2 |
D | 2:1 |
→ 60% invited guests are males i.e., 60 males
→ 40% invited guests are females i.e., 40 females
→ 80% invited guests are attended i.e., total guests attended to a party = 80
→ All the invited females are attended then remaining people are males = 80 – 40 = 40 males
⇒ 40 males : 40 females
⇒ 1 : 1
Question 28 |
In appreciation of the social improvements completed in a town, a wealthy philanthropist decided to gift Rs 750 to each male senior citizen in the town and Rs 1000 to each female senior citizen. Altogether, there were 300 senior citizens eligible for this gift. However, only 8/9th of the eligible men and 2/3rd of the eligible women claimed the gift. How much money (in Rupees) did the philanthropist give away in total?
A | 1,50,000 |
B | 2,00,000 |
C | 1,75,000 |
D | 1,51,000 |
Female senior citizen’s gift = Rs. 1000
No. of males = a say
No. of females = b say
Altogether no. of persons eligible for gift = 300
i.e., a+b = 300
Total amount be given = (8x/9 × 750) + (2y/3 × 1000)
= (2000x/3) + (2000y/3)
= 2000/3 (x+y)
= 2000/3 (300)
= 2,00,000
Question 29 |
A six sided unbiased die with four green faces and two red faces is rolled seven times. Which of the following combinations is the most likely outcome of the experiment?
A | Three green faces and four red faces. |
B | Four green faces and three red faces. |
C | Five green faces and two red faces. |
D | Six green faces and one red face. |
→ If we roll a die for six time then we get 4 green faces and 2 red faces.
→ And if we roll for seventh time green face can have more probability to become a outcome.
→ Then most likely outcome is five green faces and two red faces.
Question 30 |
Out of a group of 21 persons, 9 eat vegetables, 10 eat fish and 7 eat eggs : 5 persons eat all three. How many persons eat at least two out the three dishes?
A | Theory Explanation. |
Question 31 |
A | fair / fare
|
B | faer / fair
|
C | fare / fare
|
D | fare / fair
|
E |
Question 32 |
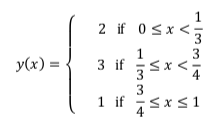
Which one of the following is the area under the curve for the interval [0, 1] on the x-axis?
A | 5/6 |
B | 6/5 |
C | 13/6 |
D | 6/13 |
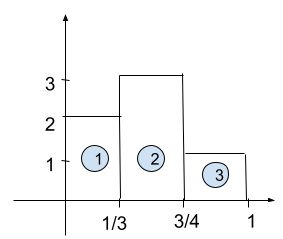
We know that area of a rectangle = length * breadth = L * B
Area of rectangle (1) = L*B = (1/3) * 2 = (2/3)
Area of rectangle (2) = L*B = (3/4 - 1/3 ) * 3 = (5/4 )
Area of rectangle (3) = L*B = (1 - 3/4) * 1 = 1/4
Therefore Total area = Area(1+2+3) = (2/3) + (5/4) + (1/4) = 26/12 = 13/6
Question 33 |
A | 51 |
B | -51 |
C | 126 |
D | -126 |
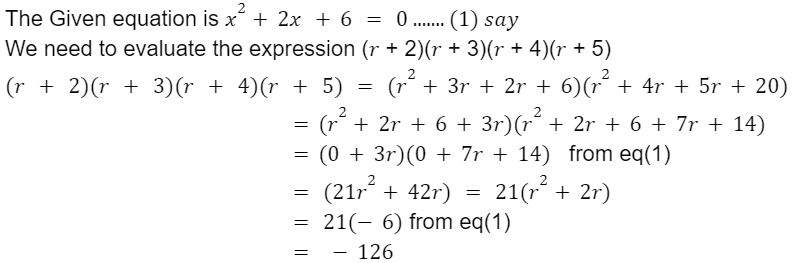
Question 34 |
Statement 1: All students are inquisitive.
Statement 2: Some students are inquisitive.
Statement 3: No student is inquisitive.
Statement 4: Some students are not inquisitive.
From the given four statements, find the two statements that CANNOT BE TRUE simultaneously, assuming that there is at least one student in the class.
A | Statement 1 and Statement 3 |
B | Statement 1 and Statement 2 |
C | Statement 2 and Statement 4 |
D | Statement 3 and Statement 4 |
Statement 1: All students are inquisitive. Statement 3: No student is inquisitive
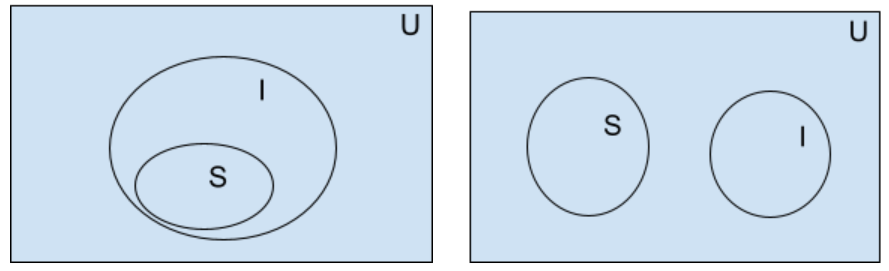
Question 35 |
From the additional plates given in the options, which one of the combinations of additional plates would allow the player to construct a five-letter palindrome. The player should use all the five plates exactly once. The plates can be rotated in their plane.
A |  |
B |  |
C | 
|
D |  |
E |
Option 2: A,D,R,A,R from these we can form RADAR which is a palindrome.
Option 3: A,D,Z,E,D from these letters we can't form a palindrome.
Option 4: A,D,I,L,Y from these letters we can't form a palindrome.
Question 36 |
Some others believe that “what gets measured, gets gamed”.
One possible reason for the difference in the beliefs is the work culture in organizations. In organizations with good work culture, metrics help improve outcomes.
However, the same metrics are counterproductive in organizations with poor work culture.
Which one of the following is the CORRECT logical inference based on the information in the above passage?
A | Metrics are useful in organizations with poor work culture |
B | Metrics are useful in organizations with good work culture |
C | Metrics are always counterproductive in organizations with good work culture |
D | Metrics are never useful in organizations with good work culture |
Option B: Metrics are useful in organizations with good work culture. Which is correct and relevant to the considered sentence.
Option C: Metrics are always counterproductive in organizations with good work culture. Which is incorrect because we can't always guarantee good work culture.
Option D: Metrics are never useful in organizations with a good work culture. Incorrect metrics will help to make a good work culture.
Question 37 |
A | Equal number of boys and girls qualified |
B | Equal number of boys and girls appeared for the test |
C | The number of boys who appeared for the test is less than the number of girls
who appeared
|
D | The number of boys who qualified the test is less than the number of girls who
Qualified
|
60% can be written as ⅗. Which means among 5 qualified persons three of them are girls.
So, The number of boys qualified is less than the number of girls qualified.
Question 38 |
A | 1/2 |
B | 8/25 |
C | 19/50 |
D | 23/50 |
Probability of first ball is green = 3/5
If the first ball is green then we are not replacing so the probability of the second ball being orange is = 2/4.
Probability of first ball green and second ball orange is =3/5 * 2/4 = 6/20
Case 2: The first ball is orange
Probability of first ball is orange =2/5
If the first ball is orange then we are replacing it with another orange ball/ so the number balls will remain the same.
Probability of second ball is orange = 2/5
Probability of first ball is orange and second ball is also orange = 2/5*2/5 = 4/25
Therefore, Total probability = (6/20 + 4/25) = 23/50.
Question 39 |
The line joining P and R is parallel to the line joining Q and S.
P is placed on the side opposite to the corner T.
S and U cannot be placed on the same side.
Which one of the following statements is correct based on the above information?
A | P cannot be placed at a corner |
B | S cannot be placed at a corner |
C | U cannot be placed at a mid-point |
D | R cannot be placed at a corner |
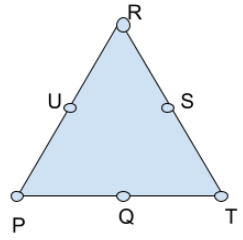
The Image is satisfying all given conditions. From this we can say that S cannot be placed at the corner. By satisfying all given conditions we can draw in different ways but in all cases S cannot be placed at the corner.
Question 40 |
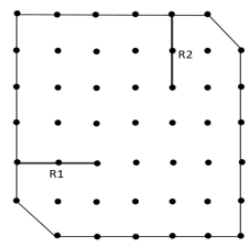
What is the least number of additional straight ropes needed to create the desired plots? A single rope can pass through three poles that are aligned in a straight line.
A | 2 |
B | 4 |
C | 5 |
D | 3 |
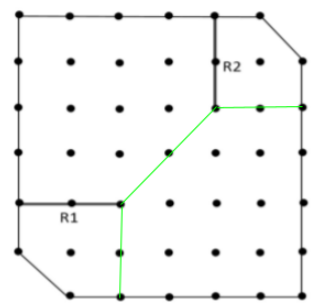
Therefore least number of additional ropes required = 3.
Question 41 |
(i) Everybody in the class is prepared for the exam.
(ii) Babu invited Danish to his home because he enjoys playing chess.
Which of the following is the CORRECT observation about the above two sentences?
A | (i) is grammatically incorrect and (ii) is ambiguous |
B | (i) is grammatically correct and (ii) is ambiguous |
C | (i) is grammatically correct and (ii) is unambiguous |
D | (i) is grammatically incorrect and (ii) is unambiguous |
ii). Babu invited Danish to his home because he enjoys playing chess.
This statement is ambiguous as there is no guarantee that Danish knows playing chess.
Question 42 |
| Items | Cost (₹) | Profit % | Marked Price (₹) |
| P | 5,400 | --- | 5,860 |
| Q | --- | 25 | 10,000 |
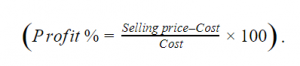
The discount on item Q, as a percentage of its marked price, is ______.
A | 25 |
B | 5 |
C | 10 |
D | 12.5 |
Question 43 |
A | 37 |
B | 73 |
C | 21 |
D | 50 |
Number of boys = 7x
Number of girls = 3x
Total number of students = 10x
So the possible value should multiple by 10.
Answer is 50.
Question 44 |
Which one of the following is NOT a convex polygon?
A |  |
B |  |
C |  |
D |  |
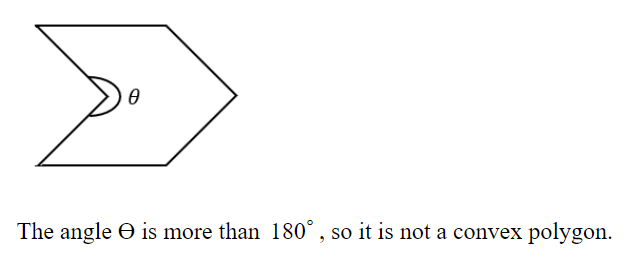
Question 45 |
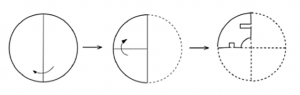
A circular sheet of paper is folded along the lines in the directions shown. The paper, after being punched in the final folded state as shown and unfolded in the reverse order of folding, will look like _______.
A | 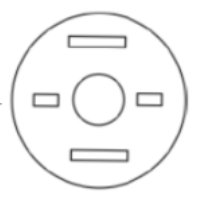 |
B |  |
C | 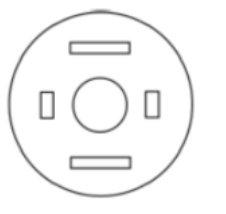 |
D | 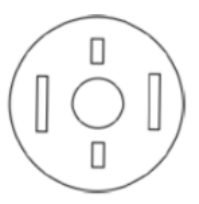 |

Question 46 |
A | 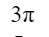 |
B | 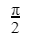 |
C | 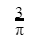 |
D | 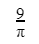 |
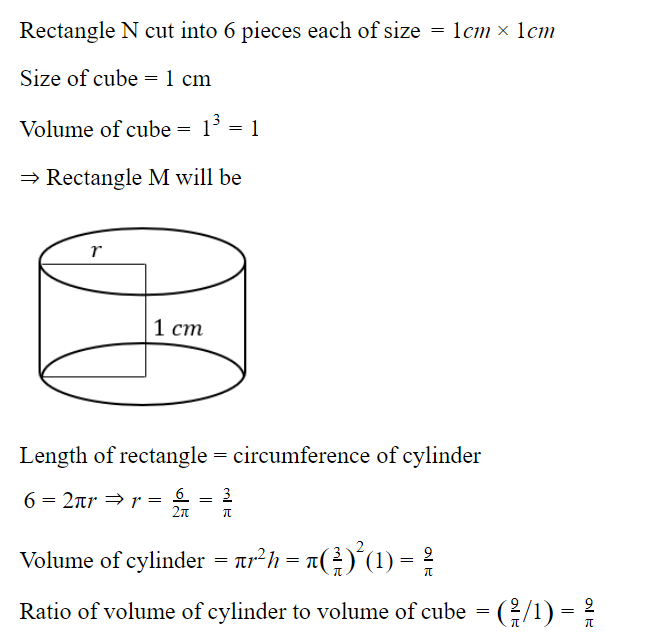
Question 47 |
Which one of the following options maintains a similar logical relation in the above sentence?
A | Hospital, library |
B | Medicine, grammar |
C | Plan, outline |
D | Doctor, book |
Doctor is to surgery as writer is to book.
Question 48 |
A | 0.81225 |
B | 0.4235 |
C | 0.6976 |
D | 0.3024 |
There are 5 bags having identical sets of 10 distinct chocolates. one chocolate is drawn from each bag, probability to find at least 2 chocolate is identical
The total number of such selections possible = 10*10*10*10*10 = 10^5.
We need to select such that at least two of them are identical.
We can count the number of ways with no chocolate being repeated and subtract it from total possible ways to get the required probability.
The number of ways to select all different/distinct = 10*9*8*7*6
Required number of selections= 10^5-10*9*8*7*6 = 69760
Required probability = 69760/10^5 = 0.69760
Question 49 |
Which one of the following statements summarizes the passage?
A | AOM are addressing the problem superficially. |
B | The proposed AOM addresses the core problems that cause obesity. |
C | AOM are addressing the core problems and are likely to succeed. |
D | If obesity reduces, poverty will naturally reduce, since obesity causes poverty. |
Question 50 |
Statement I: All bacteria are microorganisms.
Statement II: All pathogens are microorganisms.
Conclusion I: Some pathogens are bacteria.
Conclusion II: All pathogens are not bacteria.
Based on the above statements and conclusions, which one of the following options is logically CORRECT?
A | Only conclusion I is correct |
B | Only conclusion II is correct |
C | Neither conclusion I nor II is correct |
D | Either conclusion I or II is correct |
