TIFR 2021
Question 1 |
A box contains 5 red marbles, 8 green marbles, 11 blue marbles, and 15 yellow
marbles. We draw marbles uniformly at random without replacement from the box.
What is the minimum number of marbles to be drawn to ensure that out of the
marbles drawn, at least 7 are of the same colour?
7 | |
8 | |
23 | |
24 | |
39 |
Question 2 |
The maximum area of a rectangle inscribed in the unit circle (i.e., all the vertices of
the rectangle are on the circle) in a plane is:
1 | |
2 | |
3 | |
4 | |
5 |
Question 3 |
Let M be an n m real matrix. Consider the following:
* Let k1 be the smallest number such that M can be factorized as AB, where A is an n x k1 and B is a k1 x m matrix.
*Let k2 be the smallest number such that M = Pk2 i=1 uivi, where each ui is an Nx1 matrix and each vi is an 1 x m matrix.
* Let k3 be the column-rank of M.
Which of the following statements is true?
* Let k1 be the smallest number such that M can be factorized as AB, where A is an n x k1 and B is a k1 x m matrix.
*Let k2 be the smallest number such that M = Pk2 i=1 uivi, where each ui is an Nx1 matrix and each vi is an 1 x m matrix.
* Let k3 be the column-rank of M.
Which of the following statements is true?
k11 < k2 < k3 | |
k11 < k3 < k2 | |
k2 = k3 < k1 | |
k1 = k2 = k3 | |
No general relationship exists among k1; k2 and k3. |
Question 4 |
What is the probability that at least two out of four people have their birthdays in
the same month, assuming their birthdays are uniformly distributed over the twelve
months?
25/48 | |
5/5 | |
5/12 | |
41/96 | |
55/96 |
Question 5 |
A matching in a graph is a set of edges such that no two edges in the set share a
common vertex. Let G be a graph on n vertices in which there is a subset M of
m edges which is a matching. Consider a random process where each vertex in the
graph is independently selected with probability 0 < p < 1 and let B be the set of
vertices so obtained. What is the probability that there exists at least one edge from
the matching M with both end points in the set B?
P2 | |
1-(1-P2)m | |
P2m | |
(1-P2)m | |
1-(1-p(1-p))m |
Question 6 |
Let d be the number of positive square integers (that is, it is a square of some integer)
that are factors of 205 X 215. Which of the following is true about d?
50 | |
100 < d < 150 | |
150 | |
200 | |
300 < d |
Question 7 |
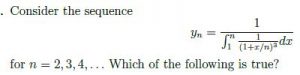
The sequence fyng does not have a limit as n ! 1. | |
yn < 1 for all n = 2; 3; 4; : : : | |
limn!1 yn exists and is equal to 6=2. | |
limn!1 yn exists and is equal to 0. | |
The sequence {yn} first increases and then decreases as n takes values 2; 3; 4; : : : |
Question 8 |
Fix n > 6. Consider the set C of binary strings x1x2... xn of length n such that the bits satisfy the following set of equalities, all modulo 2: xi + xi+1 + xi+2 = 0 for all 1 < i < n - 2, xn-1 + xn + x1 = 0, and xn + x1 + x2 = 0. What is the size of the set C?
1 for all n > 6 | |
1 for all n >6 | |
0 for all n> 6 | |
If n > 6 is divisible by 3 then |C|= 1. If n > 6 is not divisible by 3 then |C| = 4. | |
If n > 6 is divisible by 3 then |C| = 4. If n > 6 is not divisible by 3 then |C| = 1. |
Question 9 |
Lavanya and Ketak each flip a fair coin n times. What is the probability that Lavanya
sees more heads than Ketak? In the following, the binomial coefficient (n/k) counts the number of k-element subsets of an n-element set.
1/2 | |
https://solutionsadda.in/wp-content/uploads/2021/12/zinc-8.jpg |
Question 10 |
Find the following sum.

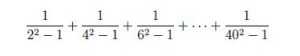
20/41 | |
10/41 | |
10/21 | |
20/21 | |
1 |
Question 11 |
How many numbers in the range f0; 1; : : : ; 1365g have exactly four 1’s in their binary
representation? (Hint: 136510 is 101010101012, that is, 1365 = 210 + 28 + 26 + 24 + 22 + 20🙂
In the following, the binomial coefficient (n/k) counts the number of k-element subsetsof an n-element set.
(6/4) | |
(10/4) | |
(10/4) + (8/3) + (6/2) + (5/1) | |
(11/4) + (9/3) + (7/2) + (5/1) | |
1024 |
There are 11 questions to complete.
