TIFR PHD CS & SS 2013
Question 1 |
An infinite two-dimensional pattern is indicated below.

The smallest closed figure made by the lines is called a unit triangle. Within every unit triangle, there is a mouse. At every vertex there is a laddoo.
What is the average number of laddoos per mouse?

The smallest closed figure made by the lines is called a unit triangle. Within every unit triangle, there is a mouse. At every vertex there is a laddoo.
What is the average number of laddoos per mouse?
3 | |
2 | |
1 | |
1/2 | |
1/3 |
Question 2 |
Consider the following two types of elections to determine which of two parties A and B forms the next government in the 2014 Indian elections. Assume for simplicity an Indian population of size 545545(= 545*1001). There are only two parties A and B and every citizen votes.
TYPE C: The country is divided into 545 constituencies and each constituency has 1001 voters. Elections are held for each constituency and a party is said to win a constituency if it receive a majority of the vote in that constituency. The party that wins the most constituencies forms the next government.
TYPE P: There are no constituencies in this model. Elections are held throughout the country and the party that wins the most votes (among 545545 voters) forms the government.
Which of the following is true?
TYPE C: The country is divided into 545 constituencies and each constituency has 1001 voters. Elections are held for each constituency and a party is said to win a constituency if it receive a majority of the vote in that constituency. The party that wins the most constituencies forms the next government.
TYPE P: There are no constituencies in this model. Elections are held throughout the country and the party that wins the most votes (among 545545 voters) forms the government.
Which of the following is true?
If a party forms the govt. by election TYPE C winning at least two-thirds of the constituencies, then
it will also form the govt. by election TYPE P. | |
If a party forms the govt. by election TYPE C, then it will also form the govt. by election TYPE P | |
If a party forms the govt. by election TYPE P, then it will also form the govt. by election TYPE C | |
All of the above | |
None of the above |
Question 3 |
Three candidates, Amar, Birendra and Chanchal stand for the local election. Opinion polls are conducted and show that fraction a of the voters prefer Amar to Birendra, fraction b prefer Birendra to Chanchal and fraction c prefer Chanchal to Amar. Which of the following is impossible?
(a, b, c) = (0.51, 0.51, 0.51); | |
(a, b, c) = (0.61, 0.71, 0.67); | |
(a, b, c) = (0.68, 0.68, 0.68); | |
(a, b, c) = (0.49, 0.49, 0.49); | |
None of the above. |
Question 4 |
A biased coin is tossed repeatedly. Assume that the outcomes of different tosses are independent and probability of heads is 2/3 in each toss. What is the probability of obtaining an even number of heads in 5 tosses, zero being treated as an even number?
121/243 | |
122/243 | |
124/243 | |
125/243 | |
128/243 |
Question 5 |
The late painter Maqbool Fida Husain once coloured the surface of a huge hollow steel sphere, of radius 1 metre, using just two colours, red and blue. As was his style however, both the red and blue areas were a bunch of highly irregular disconnected regions. The late sculptor Ramkinkar Baij then tried to fit in a cube inside the sphere, the eight vertices of the cube touching only red coloured parts of the surface of the sphere. Assume π = 3.14 for solving this problem. Which of the following is true?
Baij is bound to succeed if the area of the red part is 10 sq. metres; | |
Baij is bound to fail if the area of the red part is 10 sq. metres; | |
Baij is bound to fail if the area of the red part is 11 sq. metres; | |
Baij is bound to succeed if the area of the red part is 11 sq. metres; | |
None of the above. |
Question 6 |
You are lost in the national park of Kabrastan. The park population consists of tourists and kabrastanis. Tourists comprise two-thirds of the population the park, and give a correct answer to requests for directions with probability 3/4. The air of Kabrastan has an amnesaic quality however, and so the answers to repeated questions to tourists are independent, even if the question and the person are the same. If you ask a Kabrastani for directions, the answer is always wrong.
Suppose you ask a randomly chosen passer-by whether the exit from the park is East or West. The answer is East. You then ask the same person again, and the reply is again East. What is the probability of East being correct?
Suppose you ask a randomly chosen passer-by whether the exit from the park is East or West. The answer is East. You then ask the same person again, and the reply is again East. What is the probability of East being correct?
1/4 | |
1/3 | |
1/2 | |
2/3 | |
3/4 |
Question 7 |
For any complex number z, arg z defines its phase, chosen to be in the interval 0 ≤ arg z < 360o. If z1, z2 and z3 are three complex numbers with the same modulus but different phases (arg z3 < arg z2 < arg z1 < 180o), then the quantity

is a constant, and has the value
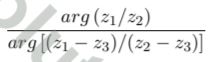
is a constant, and has the value
2 | |
1/3 | |
1 | |
3 | |
1/2 |
Question 8 |
Find the sum of the infinite series

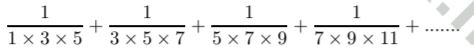
∞ | |
1/2 | |
1/6 | |
1/12 | |
1/14 |
Question 9 |
There are n kingdoms and 2n champions. Each kingdom gets 2 champions. The number of ways in which this can be done is:

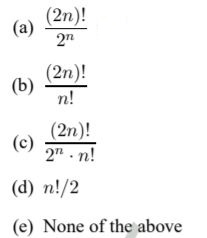
a | |
b | |
c | |
d | |
e |
Question 10 |
Three men and three rakhsasas arrive together at a ferry crossing to find a boat with an oar, but no boatman. The boat can carry one or at the most two persons, for example, one man and one rakhsasa, and each man or rakhsasa can row. But if at any time, on any bank, (including those who maybe are in the boat as it touches the bank) rakhsasas outnumber men, the former will eat up the latter. If all have to go to the other side without any mishap, what is the minimum number of times that the boat must cross the river?
7 | |
9 | |
11 | |
13 | |
15 |
Question 11 |
Let there be a pack of 100 cards numbered 1 to 100. The ith card states: ”There are at most i − 1 true cards in this pack”. Then, how many cards of the pack contain TRUE statements?
0 | |
1 | |
100 | |
50 | |
None of the above |
Question 12 |
Among numbers 1 to 1000 how many are divisible by 3 or 7?
333 | |
142 | |
475 | |
428 | |
None of the above |
Question 13 |
Doctors A and B perform surgery on patients in stages III and IV of a disease. Doctor A has performed a 100 surgeries (on 80 stage III and 20 stage IV patients) and 80 out of her 100 patients have survived (78 stage III and 2 stage IV survivors). Doctor B has also performed 100 surgeries (on 50 stage III and 50 stage IV patients). Her success rate is 60/100 (49 stage III survivors and 11 stage IV survivors). A patient has been advised that she is equally likely to be suffering from stage III or stage IV of this disease.
Which doctor would you recommend to this patient and why?
Which doctor would you recommend to this patient and why?
Doctor A since she has a higher success rate | |
Doctor A since she specializes in stage III patients and the success of surgery in stage IV patients is
anyway too low | |
Doctor B since she has performed more stage IV surgeries | |
Doctor B since she appears to be more successful | |
There is not enough data since the choice depends on the stage of the disease the patient is suffering
from |
Question 14 |
An unbiased die is thrown n times. The probability that the product of numbers would be even is
1/(2n) | |
1/[(6n)!] | |
1 − 6−n | |
6−n | |
None of the above |
Question 15 |

a | |
b | |
c | |
d | |
e |
There are 15 questions to complete.
