BFS-and-DFS
Question 1 |
Consider a complete binary tree with 7 nodes, Let A denote the set of first 3 elements obtained by performing Breadth-First Search (BFS) starting from the root. Let B denote the set of first 3 elements obtained by performing Depth-First Search (DFS) starting from the root.
The value of |A - B| is _______.
1 |
Question 1 Explanation:
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible.
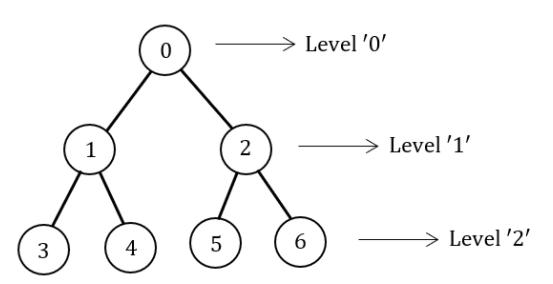

A={0,1,2} → BFS
The BFS traverse through level by level.
DFS:
B={0,1,3}
B={0,1,4}
B={0,2,6}
B={0,2,5}
The DFS starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.
|A-B| = 1
Note: The cardinality of set A-B is 1.
Question 2 |
An articulation point in a connected graph is a vertex such that removing the vertex and its incident edges disconnects the graph into two or more connected components.
Let T be a DFS tree obtained by doing DFS in a connected undirected graph G.
Which of the following options is/are correct?
- Root of T can never be an articulation point in G.
- If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.
- A leaf of T can be an articulation point in G.
- Root of T is an articulation point in G if and only if it has 2 or more children
4 |
Question 2 Explanation:
Statement-1: FALSE: Root of T can never be an articulation point in G.
Statement-2:
Example-1:
If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.
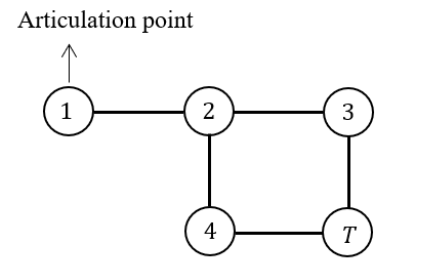
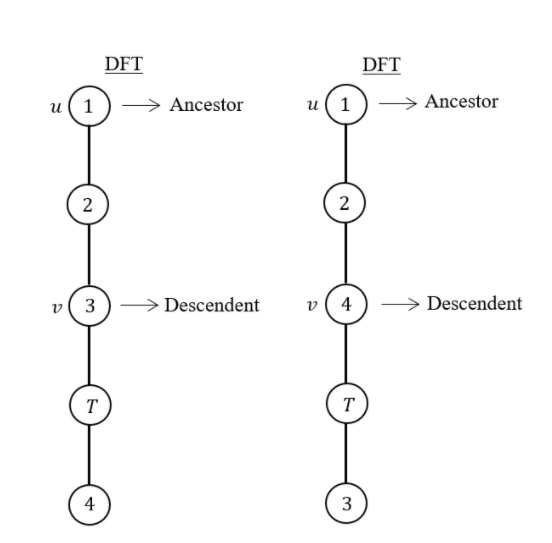

Here 2 and 6 are articulation points. If you consider node-1 ancestor and node-3 descendent, then without passing through from node -2, there exists a path from one node to another node.
Path from node-1 to node-3 If you consider node-5 ancestor and node-4 descendent, then without passing through from node-6, there exists a path from one node to another node.
Path from node-4 to node-5
The given statement is not TRUE for all cases. So, the given statement is FALSE.
Statement-3: FALSE: Leafs of a DFS-tree are never articulation points.
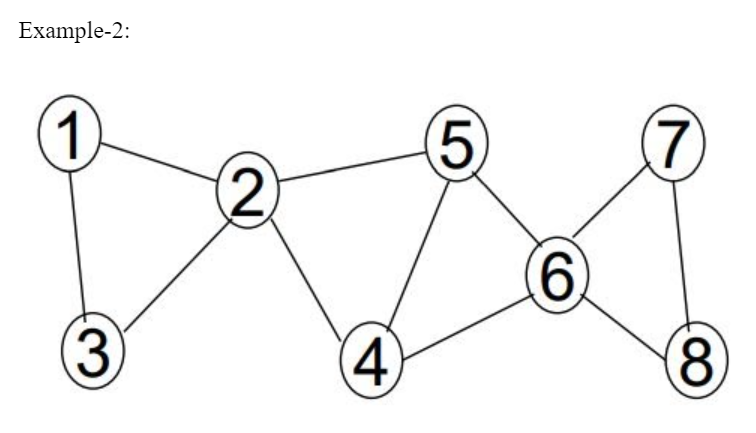
Statement-4: TRUE: The root of a DFS-tree is an articulation point if and only if it has at least two children.
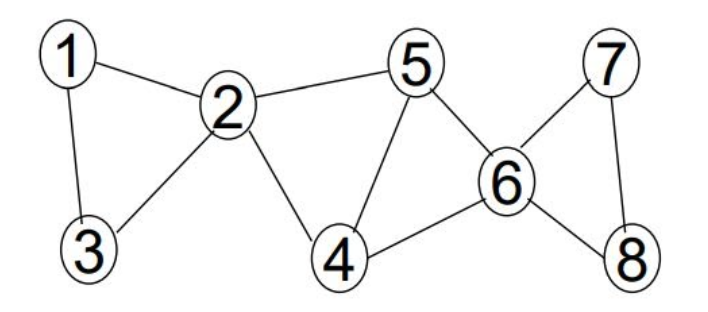
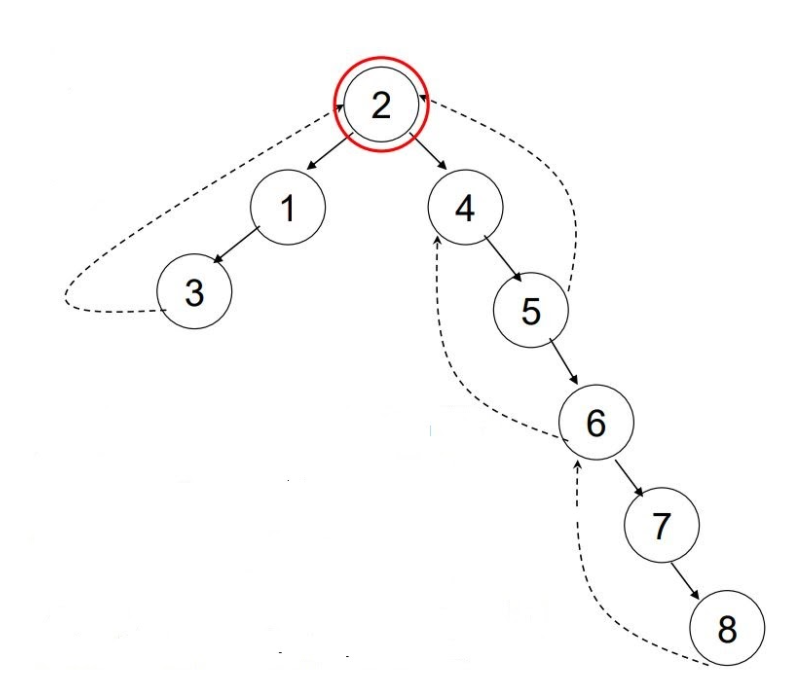
Node 2 is an AP because any node from the first subtree (1, 2) is connected to any node from the second subtree (4, 5, 6, 7, 8) by a path that includes node 2. If node 2 is removed, the 2 subtrees are disconnected.
Statement-2:
Example-1:
If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.




Here 2 and 6 are articulation points. If you consider node-1 ancestor and node-3 descendent, then without passing through from node -2, there exists a path from one node to another node.
Path from node-1 to node-3 If you consider node-5 ancestor and node-4 descendent, then without passing through from node-6, there exists a path from one node to another node.
Path from node-4 to node-5
The given statement is not TRUE for all cases. So, the given statement is FALSE.
Statement-3: FALSE: Leafs of a DFS-tree are never articulation points.
Statement-4: TRUE: The root of a DFS-tree is an articulation point if and only if it has at least two children.


Node 2 is an AP because any node from the first subtree (1, 2) is connected to any node from the second subtree (4, 5, 6, 7, 8) by a path that includes node 2. If node 2 is removed, the 2 subtrees are disconnected.
Question 3 |
The Breadth First Search (BFS) algorithm has been implemented using the queue data structure. Which one of the following is a possible order of visiting the nodes in the graph below?
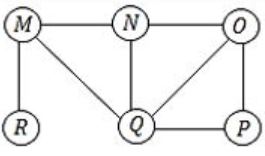
MNOPQR | |
NQMPOR | |
QMNROP | |
POQNMR |
Question 3 Explanation:
The possible order of visiting the nodes in Breadth First Search Algorithm, implementing using Queue Data Structure is
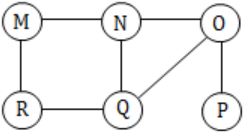
(Do it by option Elimination)
(a) MNOPQR – MNO is not the proper order R must come in between.
(b) NQMPOR – QMP is not the order O is the child of N.
(C) QMNROP – M is not the child of Q, so QMN is false.
(D) POQNMR – P → OQ → NMR is the correct sequence. Hence Option (D).

(Do it by option Elimination)
(a) MNOPQR – MNO is not the proper order R must come in between.
(b) NQMPOR – QMP is not the order O is the child of N.
(C) QMNROP – M is not the child of Q, so QMN is false.
(D) POQNMR – P → OQ → NMR is the correct sequence. Hence Option (D).
Question 4 |
Let G be a directed graph and T a depth first search (DFS) spanning tree in G that is rooted at a vertex v. Suppose T is also a breadth first search (BFS) tree in G, rooted at v. Which of the following statements is/are TRUE for every such graph G and tree T ?
There are no back-edges in G with respect to the tree T
| |
There are no cross-edges in G with respect to the tree T | |
There are no forward-edges in G with respect to the tree T | |
The only edges in G are the edges in T |
Question 4 Explanation:
(A) Not True: Back edges are still possible in this scenario, as explained before.
(B) Not True: While the BFS aspect reduces the likelihood of cross-edges, it's not guaranteed. Imagine a graph with a cycle that connects back to an earlier explored level. Such a cycle would create a cross-edge in G relative to T.
(C) True: In a BFS tree, all vertices at a level are explored before moving to the next level. This ensures that for any two connected vertices in G:
If they are in the same level of T, there cannot be a forward edge because BFS explores neighbors at a level before moving deeper (they would be explored in the opposite order if it were a forward edge).
If one vertex is an ancestor of the other in T, it cannot be a forward edge by definition (a forward edge points from a vertex to its descendant).
Therefore, since T is both a DFS spanning tree and a BFS tree rooted at v, all edges in T must be either back edges (pointing to an ancestor) or edges that explore neighbors at the same level. This eliminates the possibility of forward edges in G with respect to T.
There are 4 questions to complete.
