Boolean-Algebra
Question 1 |
What values of A, B, C and D satisfy the following simultaneous Boolean equations?
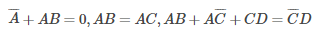
A = 1, B = 0, C = 0, D = 1 | |
A = 1, B = 1, C = 0, D = 0 | |
A = 1, B = 0, C = 1, D = 1 | |
A = 1, B = 0, C = 0, D = 0 |
Question 2 |
The simultaneous equations on the Boolean variables x, y, z and w,
x + y + z = 1
xy = 0
xz + w = 1
xy +  = 0
= 0
have the following solution for x, y, z and w, respectively.
0 1 0 0 | |
1 1 0 1 | |
1 0 1 1 | |
1 0 0 0 |
Question 3 |
The Boolean function x'y' + xy + x'y is equivalent to
x' + y' | |
x + y | |
x + y' | |
x' + y |
= x'y' + x'y + xy
= x'(y'+y)+xy
= x'⋅1+xy
= x'+xy
= (x'+x)(x'+y)
= 1⋅(x'+y)
= x'+y
Question 4 |
The number of min-terms after minimizing the following Boolean expression is ______.
[D′ + AB′ + A′C + AC′D + A′C′D]′
1 | |
2 | |
3 | |
4 |
[D' + AB' + A'C + AC'D + A'C'D]'
[D' + AB' + A'C + C'D (A + A')']' (since A+A' = 1)
[AB' + A'C + (D' + C') (D' + D)]' (since D' + D =1)
[AB' + A'C + D' + C']'
[AB' + (A' + C') (C + C') + D']'
[AB' + A' + C' + D']'
[(A + A') (A' + B') + C' + D']'
[A' + B' + C' + D']'
Apply de-morgan's law,
ABCD
Question 5 |
Let, x1⊕x2⊕x3⊕x4 = 0 where x1, x2, x3, x4 are Boolean variables, and ⊕ is the XOR operator. Which one of the following must always be TRUE?
x1x2x3x4 = 0 | |
x1x3+x2 = 0 | |
 | |
x1 + x2 + x3 + x4 = 0 |
x1 ⊕ x2 ⊕ x3 ⊕ x4 = 0 -----(1)
A) x1x2x3 x4 = 0
Put x1 = 1, x2 = 1, x3 = 1, x4 = 1
The given equation will be zero, i.e.,
1 ⊕ 1 ⊕ 1 ⊕ 1 = 0
But,
x1x2x3 x4 ≠ 0
So, false.
B) x1x3 + x2 = 0
Put x1 = 1, x2 = 1, x3 = 0 , x4 = 0
The given equation will be zero, i.e.,
1 ⊕ 1 ⊕ 0 ⊕ 0 = 0
But,
x1x3 + x2 ≠ 0
So, false.
D) x1 + x2 + x3 + x4 = 0
Let x1=1, x2=1, x3=0, x4=0
The given equation will be zero, i.e.,
1 ⊕ 1 ⊕ 0 ⊕ 0 = 0
But,
x1 + x2 + x3 + x4 ≠ 0
So, false.
(i) True.
Question 6 |
Consider the Boolean operator with the following properties:
Then x#y is equivalent to
 | |
 | |
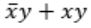 | |
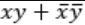 |
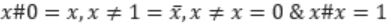
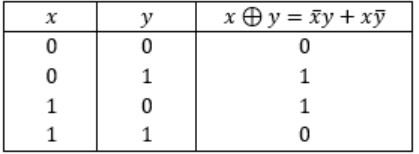
Ex-OR satisfies all the properties. Hence,
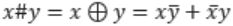
Question 7 |
The minterm expansion of ![]() is
is
m2+m4+m6+m7 | |
m0+m1+m3+m5 | |
m0+m1+m6+m7 | |
m2+m3+m4+m5 |
= PQR + PQR' + PQR' + P'QR' + PQR' + PQ'R'
= PQR + PQR' + P'QR' + PQ'R'
= m7 + m6 + m2 + m4
Question 8 |
What is the maximum number of different Boolean functions involving n Boolean variables?
n2 | |
2n | |
22n | |
2n2 |
Number of variables= n
Number of input combinations is 2n.
Each “boolean” function has two possible outputs i.e 0 and 1.
Number of boolean functions possible is 22n.
Formula: The number of m-ary functions possible with n k-ary variables is mkn.
Question 9 |
The simplified SOP (sum of product) form of the boolean expression
![]()
 | |
 | |
 | |
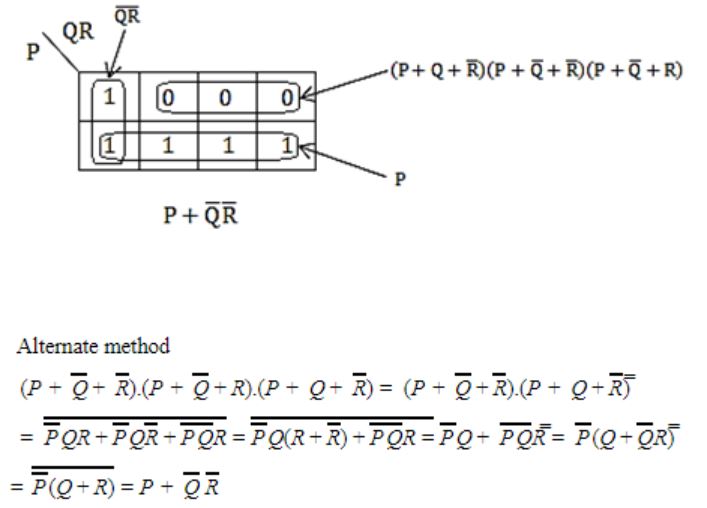
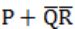 |
Question 10 |
The truth table
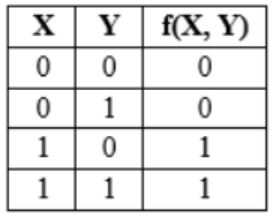
represents the Boolean function
X | |
X + Y | |
X ⊕ Y | |
Y |
Question 11 |
If P, Q, R are Boolean variables, then
Simplifies to
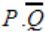 | |
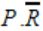 | |
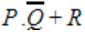 | |
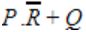 |

Question 12 |
Consider the following Boolean expression for F:
F(P, Q, R, S) = PQ + P'QR + P'QR'S
The minimal sum-of-products form of F is
 | |
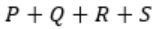 | |
 | |
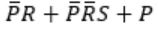 |
= Q(P+P’R) + P’QR’S
= Q(P+R) + P’QR’S
= QP + QR + P’QR’S
= QP + Q(R + P’R’S)
= QP + Q( R + P’S)
= QP + QR + QP’S
= Q(P+P’S) + QR
= Q(P+S)+ QR
= QP + QS + QR
Question 13 |
0 | |
1 | |
-1 | |
None |

