Boolean-Expression
Question 1 |
Let * be defined as x * y = x' + y. Let z = x * y. Value of z * x is
x'+y | |
x | |
0 | |
1 |
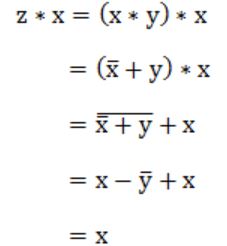
Question 2 |
Let f(A,B) = A' + B. Simplified expression for function f(f(x + y, y)z) is:
x'+z | |
xyz | |
xy'+z | |
None of the above |
⇒ f(f((x+y), y), z)
⇒ f(((x+y)' + y), z)
⇒ f(((x'⋅y') + y), z)
⇒ f((x'⋅y') + y), z)
⇒ ((x'⋅y') + y)' + z
⇒ (x'⋅y')⋅y' + z
⇒ (x+y)⋅y' + z
⇒ (xy'+yy') + z
⇒ xy' + z
Question 3 |
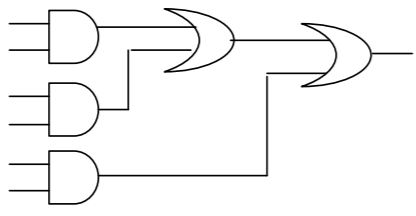
(a) Express the function f(x,y,z) = xy' + yz' with only one complement operation and one or more AND/OR operations. Draw the logic circuit implementing the expression obtained, using a single NOT gate and one or more AND/OR gates.
(b) Transform the following logic circuit (without expressing its switching function) into an equivalent logic circuit that employs only 6 NAND gates each with 2-inputs.
Theory Explanation is given below. |

(A) f(x,y,z) = xy' +yz'
It is not possible to express only one NOT gate.
Question 4 |
If w, x, y, z are Boolean variables, then which one of the following is INCORRECT?
wx + w(x + y) + x(x + y) = x + wy | |
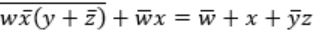 | |
 | |
(w + y)(wxy + wyz) = wxy + wyz |
wx + w(x + y) + x(x + y)
= (wx + wx) + wy + (x + xy)
= wx + wy + x(1 + y)
= wx + wy + x
= (w + 1)x + wy
= x + wy
Option-B:
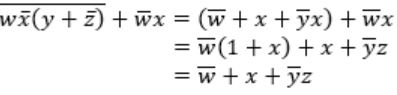
Option-C:
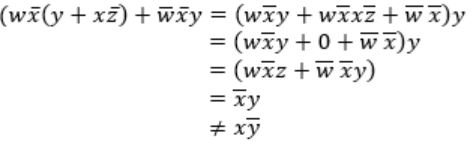
Option-D:
(w + y)(wxy + wyz) = wxy + wyz + wxy + wyz = wxy + wyz
Question 5 |
Which one of the following is NOT a valid identity?
(x + y) ⊕ z = x ⊕ (y + z) | |
(x ⊕ y) ⊕ z = x ⊕ (y ⊕ z) | |
x ⊕ y = x + y, if xy = 0 | |
x ⊕ y = (xy + x'y')' |
(x+y) ⊕ z = (1+1)⊕ 0 = 1 ⊕ 0 = 1
x ⊕ (y+z) = 1⊕(1+0) = 1 ⊕ 1 = 0
So,
(x+y) ⊕ z ≠ x ⊕ (y+z)
Question 6 |
Let f(w, x, y, z) = ∑(0, 4, 5, 7, 8, 9, 13, 15). Which of the following expressions are NOT equivalent to f?
- (P) x'y'z' + w'xy' + wy'z + xz
(Q) w'y'z' + wx'y' + xz
(R) w'y'z' + wx'y' + xyz + xy'z
(S) x'y'z' + wx'y' + w'y
P only
| |
Q and S | |
R and S | |
S only |
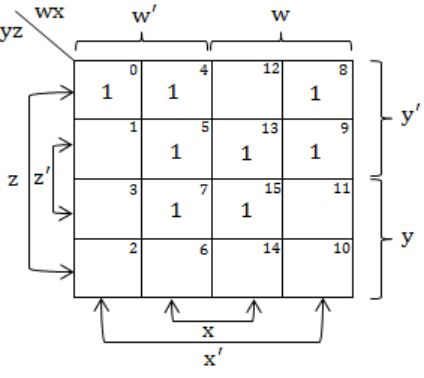
(P), (Q), (R) cover all the minterms and are equivalent to f(w,x,y,z) = Σ(0,4,5,7,8,9,13,15).
(S) covers the minterms m0, m8, m9, m2, m3, m6, m7.
(S) is not covering the minterms m4, m5, m13, m15.
Question 7 |
Define the connective * for the Boolean variables X and Y as: X * Y = XY + X'Y'. Let Z = X * Y.
Consider the following expressions P, Q and R.
P: X = Y⋆Z Q: Y = X⋆Z R: X⋆Y⋆Z = 1
Which of the following is TRUE?
Only P and Q are valid. | |
Only Q and R are valid.
| |
Only P and R are valid. | |
All P, Q, R are valid. |
= Y(XY + X’Y’) + Y’(XY+X’Y’)’
= XY+Y’(X ⊕ Y)
= XY+Y’(XY’+X’Y)
= XY+XY’
= X(Y+Y’) = X
Q: X*Z = (XZ + X’Z’)
= X(XY + X’Y’) + X’(XY + X’Y’)’
= XY+X’(X’Y+XY’)
= XY+X’Y
= (X+X’)Y = Y
R: X* Y*Z
= X*X Since P: Y*Z= X
= XX + X’X’
= 1
Question 8 |
Match the following
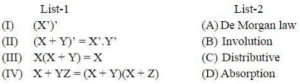
I-D, II-A, III-B.IV-C | |
I-C, II-A, III-D.IV-B | |
I-B, II-A, III-D.IV-C | |
I-B, II-D, III-A.IV-C |

Question 9 |
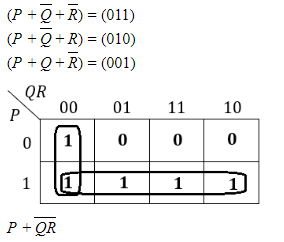
(P’ Q + R) | |
(P + Q’. R’) | |
(P’.Q + R) | |
(P. Q + R) |