Combinatorics
Question 1 |
The number of permutations of the characters in LILAC so that no character appears in its original position, if the two L’s are indistinguishable, is _______.
12 |
― ― ― ― ―
Given: L I L A C
The derangement formula ⎣n!/e⎦ cannot be directly performed as there are repeated characters.
Let’s proceed in regular manner:
The L, L can be placed in other ‘3’ places as
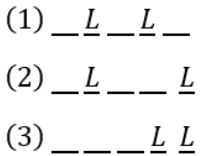
(1) Can be arranged such that A, I, C be placed in three positions excluding ‘C’ being placed at its own position, which we get only 2×2×1 = 4 ways.
Similarly (2) can be filled as A, I, C being placed such that 4th position is not filled by A, so we have 2×2×1 = 4 ways. Similarly with (3).
Totally, we get 4+4+4 = 12 ways.
Question 2 |
Which one of the following is a closed form expression for the generating function of the sequence {an}, where an = 2n+3 for all n = 0, 1, 2, …?
3/(1-x)2 | |
3x/(1-x)2 | |
2-x/(1-x)2 | |
3-x/(1-x)2 |
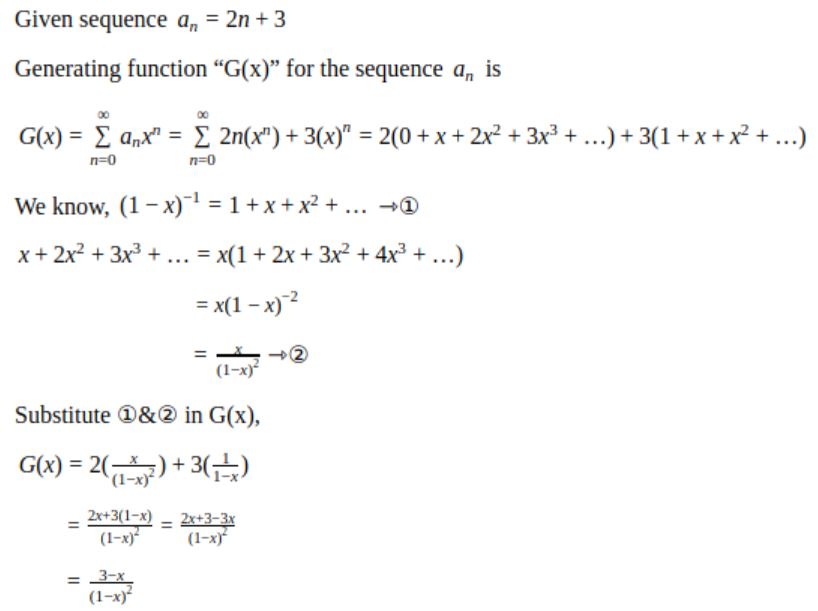
Question 3 |
The number of binary strings of n zeroes and k ones that no two ones are adjacent is
n-1Ck | |
nCk | |
nCk+1 | |
None of the above |
XOXOXOXOXOXOX
n+1 gaps can be possible, where 1's can be placed so that no two one's are adjacent. So, no. of ways in which k 1's can be placed in n+1 gaps are,
n+1Ck
Question 4 |
Two girls have picked 10 roses, 15 sunflowers and 15 daffodils. What is the number of ways they can divide the flowers amongst themselves?
1638 | |
2100 | |
2640 | |
None of the above |
n+r-1Cr-1
So for 10 roses,
10+2-1C2-1 = 11C1 = 11
For 15 sunflowers,
15+2-1C2-1 = 16C1 = 16
For 15 daffodils,
15+2-1C2-1 = 16C1 = 16
∴ The final answer is,
11×16×16 = 2816
Question 5 |
The minimum number of cards to be dealt from an arbitrarily shuffled deck of 52 cards to guarantee that three cards are from some same suit is
3 | |
8 | |
9 | |
12 |
No. of suits = 4(P)
Apply pigeon hole principal.
Then number of pigeons = n
floor [(n-1)/P] + 1 = 3
floor [(n-1)/P] = 2
floor [(n-1)] = 8
floor (n) = 8 + 1
n ≥ 9
Minimum no. of cards, n = 9
Question 6 |
How many 4-digit even numbers have all 4 digits distinct?
2240 | |
2296 | |
2620 | |
4536 |

If last digit is (2, 4, 6, 8)
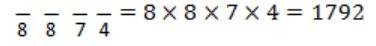
Total possibilities = 504 + 1792 = 2296
Question 7 |
(a) In how many ways can a given positive integer n ≥ 2 be expressed as the sum of 2 positive integers (which are not necessarily distinct). For example, for n = 3, the number of ways is 2, i.e., 1+2, 2+1. Give only the answer without any explanation.
(b) In how many ways can a given positive integer n ≥ 3 be expressed as the sum of 3 positive integers (which are not necessarily distinct). For example, for n = 4, the number of ways is 3, i.e., 1+2+1, 2+1+1. Give only the answer without any explanation.
(c) In how many ways can a given positive integer n ≥ k be expressed as the sum of k positive integers (which are not necessarily distinct)? Give only the answer without explanation.
Theory Explanation is given below. |
Question 8 |
n couples are invited to a party with the condition that every husband should be accompanied by his wife. However, a wife need not be accompanied by her husband. The number of different gatherings possible at the party is
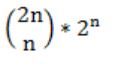 | |
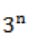 | |
 | |
 |
i) Both husband and wife comes
ii) Only wife comes
iii) Both are not come
The no. of different gatherings possible at party is
= 3 * 3 * 3 * 3 * ... n times
= 3n
Question 9 |
m identical balls are to be placed in n distinct bags. You are given that m ≥ kn, where, k is a natural number ≥1. In how many ways can the balls be placed in the bags if each bag must contain at least k balls?
 | |
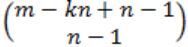 | |
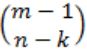 | |
 |

. So option (B) is correct.
Question 10 |
Mala has a colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour-pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?
9 | |
8 | |
7 | |
6 |
Each is printed twice the no. of letters = 26×2 = 52
If Mala has k colours, she can have k pairs of same colours.
She also can have kC2 different pairs in which each pair is having different colours.
So total no. of pairs that can be coloured = k+kC2
k+kC2 ≥ 26
k+k(k-1)/2 ≥ 26
k(k+1)/2 ≥ 26
k(k+1) ≥ 52
k(k+1) ≥ 7*8
k≥7
Question 11 |

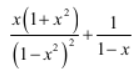 | |
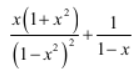 | |
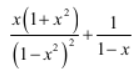 | |
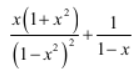 |
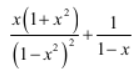
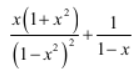
Question 12 |

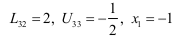 | |
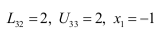 | |
 | |
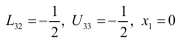 |

Given,
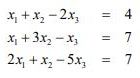
(Assume x1,x2,x3 as a,b,c)

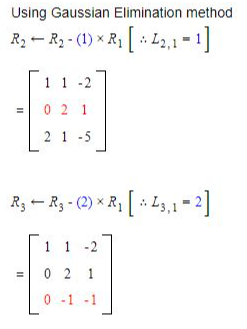

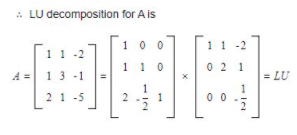


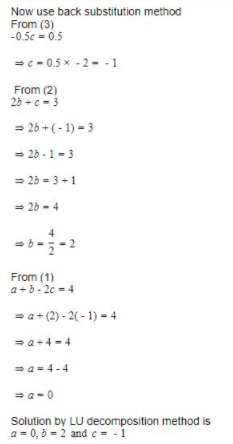
Question 13 |
Consider the sequence <xn>, n>= 0 defined by the recurrence relation xn + 1 = c . xn2- 2, where c > 0.
Suppose there exists a non-empty, open interval (a, b) such that for all x0 satisfying a < x0 < b, the sequence converges to a limit. The sequence converges to the value?
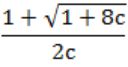 | |
 | |
2 | |
 |
Then,
x1 = c ⋅ (x0)2 - 2 = 1 ⋅ (1)2 - 2 = -1
x2 = c ⋅ (x1)2 - 2 = 1 ⋅ (-1)2 - 2 = -1
So, the value converges to -1, which is equal to
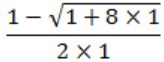
Exactly, only (B) is answer. As all the term of x converges to -1.
Question 14 |
Consider the sequence <xn>, n>= 0 defined by the recurrence relation xn + 1 = c. xn2- 2, where c > 0.
For which of the following values of c, does there exist a non-empty open interval (a,b) such that the sequence xn, converges for all x0 satisfying a < x0 (i) 0.25
(ii) 0.35
(iii) 0.45
(iv) 0.5
(i) Only | |
(i) and (ii) only | |
(i), (ii) and (iii) only | |
(i), (ii), (iii) and (iv) |
From the recurrence we should have c(xn)2 - xn - 2 < 0
For all the above values of c we have above equation as negative.
Question 15 |
The exponent of 11 in the prime factorization of 300! is
27 | |
28 | |
29 | |
30 |
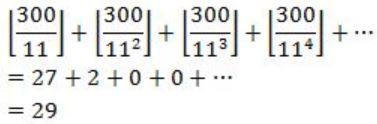
Question 16 |
In how many ways can b blue balls and r red balls be distributed in n distinct boxes?
 | |
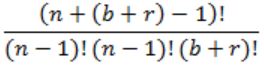 | |
 | |
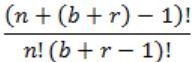 |
C(n+b-1, b) = (n+b-1)!/ (n-1)!b!
No. of red distributed to n boxes is
(n+r-1, r) = (n+r-1)!/ (n-1)!r!
Total no. of ways = (n+b-1)!/(n-1)!b! * (n+r-1)!/(n-1)!r!
= (n+b-1)!(n+r-1)!/(n-1)!b!(n-1)!r!
Question 17 |
Choose the correct alternatives (More than one may be correct).
The number of ways in which 5 A's, 5 B's and 5 C's can be arranged in a row is:15!/(5!)3 | |
15! | |
(15/5) | |
15!(5!3!) |
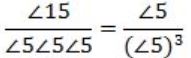
Question 18 |
Let ![]() , where |x|<1. What is g(i)?
, where |x|<1. What is g(i)?
i | |
i+1 | |
2i | |
2i |
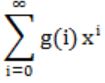
Put g(i) = i+1

S = 1 + 2x + 3x2 + 4x3 + .....
Sx = 1x + 2x2 + 3x3 + 4x4 + ......
S - Sx = 1 + x + x2 + x3 + .....
[Sum of infinite series in GP with ratio < 1 is a/1-r]
S - Sx = 1/(1-x)
S(1-x) = 1/(1-x)
S = 1/(1-x)2
Question 19 |
If the ordinary generating function of a sequence ![]() is
is ![]() , then a3 - a0 is equal to ________.
, then a3 - a0 is equal to ________.
15 | |
16 | |
17 | |
18 |
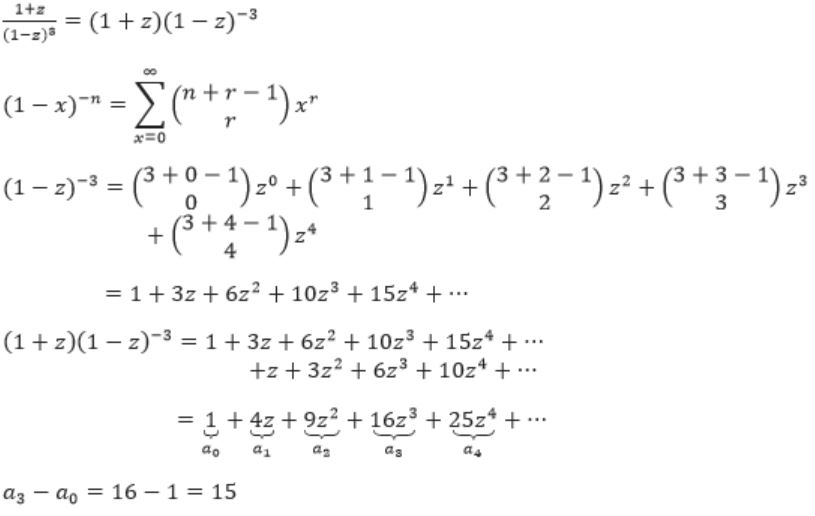
Question 20 |

is___(Rounded off to the nearest integer)
0 |
Question 21 |
The number of divisors of 2100 is ______.
36 | |
37 | |
38 | |
39 |
= 22+3×52×7 (i.e., product of primes)
Then the number of divisions of 2100 is
(2+1)∙(1+1)∙(2+1)∙(1+1) i.e., (3)(2)(3)(2) i.e., 36.
Question 22 |
Let an be the number of n-bit strings that do NOT contain two consecutive 1s. Which one of the following is the recurrence relation for an?
an = a(n-1) + 2a(n-2) | |
an = a(n-1) + a(n-2) | |
an = 2a(n-1) + a(n-2) | |
an = 2a(n-1) + 2a(n-2) |
If n=1, we have {0,1}
# Occurrences = 2
If n=2, we have {00,01,10}
# Occurrences = 3
If n=3, we have {000,001,010,100,101}
# Occurrences = 5
It is evident that a3 = a1 + a2
Similarly, an = an-1 + an-2
Question 23 |
The coefficient of x12 in (x3 + x4 + x5 + x6 + ...)3 is _________.
10 | |
11 | |
12 | |
13 |
⇒ [x3(1 + x + x2 + x3 + ...)]3
= x9(1 + x + x2 + x3 + ...)3
First Reduction:
As x9 is out of the series, we need to find the co-efficient of x3 in (1 + x + x2 + ⋯)3
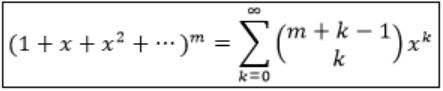
Here, m=3, k=3, the coefficient

= 5C3 = 5!/2!3! = 10
Question 24 |
Consider the recurrence relation a1 = 8, an = 6n2 + 2n + an-1. Let a99 = K × 104. The value of K is ___________.
198 | |
199 | |
200 | |
201 |
Replace a(n-1)

⇒ an = 6n2 + 2n + 6(n-1)2 + 2(n-1) + 6(n-2)2 + 2(n-2) + ⋯ a1
Given that a1 = 8, replace it
⇒ an = 6n2 + 2n + 6(n-1)2 + 2(n-1) + 6(n-2)2 + 2(n-2) + ⋯8
= 6n2 + 2n + 6(n-1)2 + 2(n-1) + 6(n-2)2 + 2(n-2) + ⋯ + 6(1)2 + 2(1)

= 6(n2 + (n-1)2 + (n-2)2 + ⋯ + 22 + 12) + 2(n + (n-1) + ⋯1)
Sum of n2 = (n(n+1)(2n+1))/6
Sum of n = (n(n+1))/2
= 6 × (n(n+1)(2n+1))/6 + 2×(n(n+1))/2
= n(n+1)[1+2n+1]
= n(n+1)[2n+2]
= 2n(n+1)2
Given a99 = k×104
a99 = 2(99)(100)2 = 198 × 104
∴k = 198
Question 25 |
4 | |
20 | |
24 | |
48 |
Question 26 |
The number of integers between 1 and 500 (both inclusive) that are divisible by 3 or 5 or 7 is _________.
271 | |
272 | |
273 | |
274 |
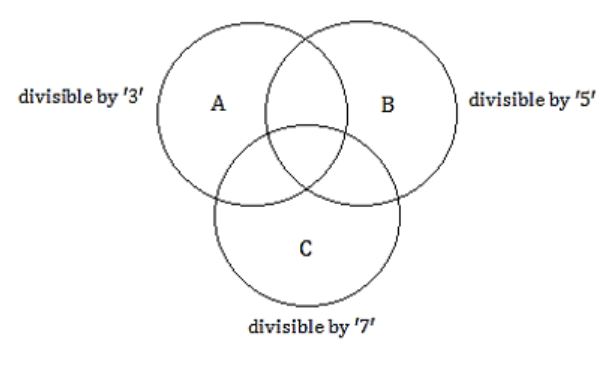
Let A = number divisible by 3
B = numbers divisible by 5
C = number divisible by 7
We need to find “The number of integers between 1 and 500 that are divisible by 3 or 5 or 7" i.e., |A∪B∪C|
We know,
|A∪B∪C| = |A|+|B|+C-|A∩B|-|A∩C|-|B∩C|+|A∩B|
|A| = number of integers divisible by 3
[500/3 = 166.6 ≈ 166 = 166]
|B| = 100
[500/5 = 100]
|C| = 71
[500/7 = 71.42]
|A∩B| = number of integers divisible by both 3 and 5 we need to compute with LCM (15)
i.e.,⌊500/15⌋ ≈ 33
|A∩B| = 33
|A∩C| = 500/LCM(3,7) 500/21 = 23.8 ≈ 28
|B∩C| = 500/LCM(5,3) = 500/35 = 14.48 ≈ 14
|A∩B∩C| = 500/LCM(3,5,7) = 500/163 = 4.76 ≈ 4
|A∪B∪C| = |A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|
= 166+100+71-33-28-14+4
= 271
Question 27 |
The number of 4 digit numbers having their digits in non-decreasing order (from left to right) constructed by using the digits belonging to the set {1, 2, 3} is _____.
15 | |
16 | |
17 | |
18 |
1 1 1 1
1 1 1 2
1 1 1 3
1 1 2 2
1 1 2 3
1 1 3 3
1 2 2 2
1 2 2 3
1 2 3 3
1 2 3 3
1 3 3 3
2 2 2 2
2 2 2 3
2 2 3 3
2 3 3 3
3 3 3 3
Hence, total 15 4-digit no. are possible.
Question 28 |
Suppose that a robot is placed on the Cartesian plane. At each step it is allowed to move either one unit up or one unit right, i.e., if it is at (i,j) then it can move to either (i+1,j) or (i,j+1).
How many distinct paths are there for the robot to reach the point (10,10) starting from the initial position (0,0)?
 | |
220 | |
210 | |
None of the above |
So now we have 10 u's and 10 r's, i.e.,
uuuuuuuuuurrrrrrrrrr
So, finally the no. of arrangements of above sequences is,
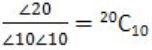
Question 29 |
Suppose that a robot is placed on the Cartesian plane. At each step it is allowed to move either one unit up or one unit right, i.e., if it is at (i,j) then it can move to either (i+1,j) or (i,j+1).
Suppose that the robot is not allowed to traverse the line segment from (4,4) to (5,4). With this constraint, how many distinct paths are there for the robot to reach (10,10) starting from (0,0)?
29 | |
219 | |
 | |
 |
So, no. of paths possible if line segment from (4,4) to (5,4) is taken is,
= paths possible from (0,0) to (4,4) * paths possible from (5,4) to (10,10)
= {uuuurrrr} * {uuuuuurrrrr}

Hence, the final answer is

Question 30 |
A pennant is a sequence of numbers, each number being 1 or 2. An n-pennant is a sequence of numbers with sum equal to n. For example, (1,1,2) is a 4-pennant. The set of all possible 1-pennants is {(1)}, the set of all possible 2-pennants is {(2), (1,1)}and the set of all 3-pennants is {(2,1), (1,1,1), (1,2)}. Note that the pennant (1,2) is not the same as the pennant (2,1). The number of 10-pennants is ________.
89 | |
90 | |
91 | |
92 |
Single two: 211111111 ⇒ 9!/8!1! = 9 pennants
Two twos: 22111111 ⇒ 8!/6!2! = 28
Three twos: 2221111 ⇒ 7!/3!4! = 35
Four twos: 222211 ⇒ 6!/4!2! = 15
Five twos: 22222 ⇒ 1
Total = 89 pennants.
Question 31 |
The number of distinct positive integral factors of 2014 is _________.
0.26 | |
0.27 | |
8 | |
0.29 |
= 2' × 19' × 53'
Now number of distinct integral factors of 2014 will be,
(1+1)×(1+1)×(1+1) = 2×2×2 = 8
